JUMP TO TOPIC [show]
 The function
The function
In this topic, we will discuss a quadratic function and how we will properly draw the graph of this function.
Is y=x^2 a Quadratic Equation?
Yes,
The function
Is y = x^2 a Parabola?
Yes,
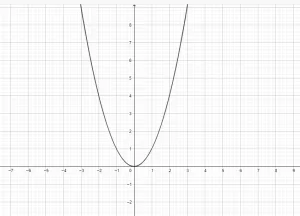
A parabola is a plane curve having a bell-shaped figure. A parabola has a directrix, a focus, and a vertex. A verticle line passes through the focus, vertex, and directrix. A parabola can be considered as a curve that lies in a cartesian plane, and the curve is defined as a moving locus, i.e., a parabola consists of a set of points equidistant from the focus of the directrix.
The point closest to the directrix is the vertex of the parabola, and the vertex can be considered as the center point of the parabola as well as it lies equidistant from the focus and the directrix. The vertex along with focus is used to determine the axis of symmetry of the parabola as it is the line that passes through focus as well as the vertex of the parabola. Another line also passes through the focus, and it is called the latus rectum; this line is also parallel to the directrix. The parabola forms a bell shape, and it is symmetric about the axis. That’s why we call it a symmetric axis. As the curve moves away from the focus, it expands. If we rotate the parabola around its axis, then it will form a paraboloid. The figure of a generic parabola is given below, and you can see that the graph of

Parabola Standard Equations and Features
Generally, the parabola are represented as
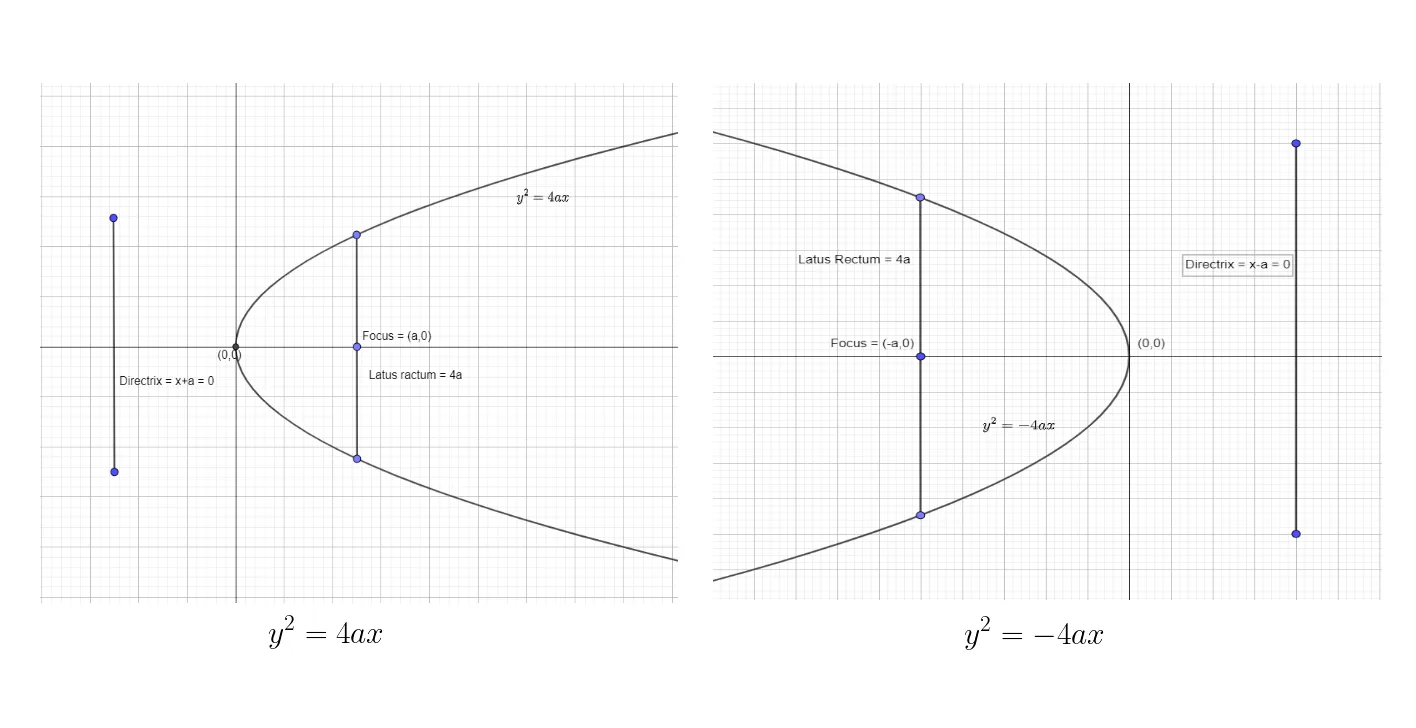
There are four standard forms of parabola according to its orientation about its axis, and these forms are represented as four different equations. The conjugate, as well as the transverse axis of these four parabolas, are different, and the characteristics of these parabolas are given in the table below.
| Standard forms | ||||
| Axis equation | ||||
| Vertex | ||||
| Directrix | ||||
| Focus Point | ||||
| Latus Rectum |
We can show the first two standard forms as:
We can show the last two standard forms as:
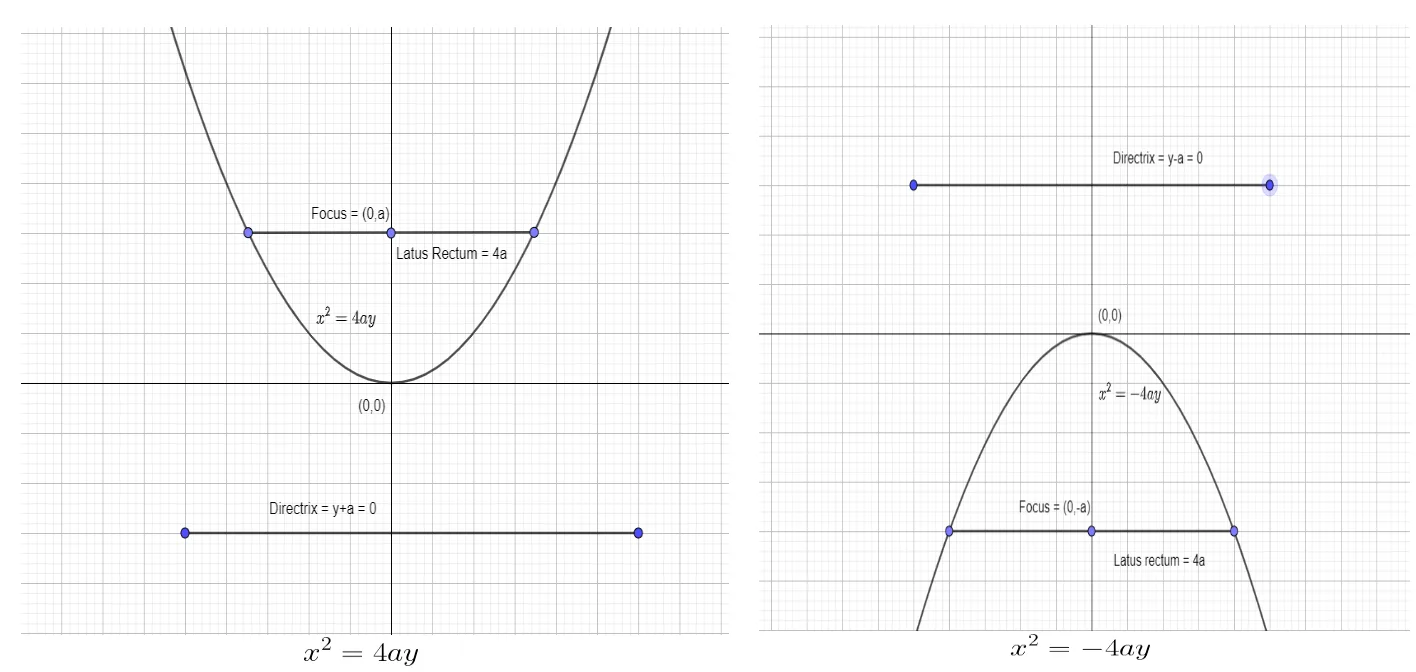
From the given table, the standard equations, and the graphs given above, one can easily make the following conclusions.
The parabola is always symmetric about its axis. If the standard equation is in the form
When the axis of symmetry is along the y-axis, then the parabola can move away from the vertex in the upward or downward direction. When the coefficient of y is negative, the parabola will expand in a downward direction, and when the coefficient of y is positive, the parabola will expand in an upward direction. For example, in our case,
When the axis of symmetry is along the x-axis, then the parabola can move away from the vertex in the right or left direction. When the coefficient of x is positive, the parabola will expand in the right direction, and when the coefficient of x is negative, the parabola will expand in the left direction. The graphical representation of this characteristic is given in the figure above.
Features of Parabola
Some of the important features of a parabola are its focus, directrix, vertex, latus rectum, focal chord, and eccentricity. Let us discuss the definition of these features with respect to the parabolic equation
Focus: The focus point for
Direction: The direction of the parabola depends upon the sign of “
Directrix: The directrix line will be parallel to the x-axis for the given standard equation, and it will pass through the point
Vertex: The point where the curve of the parabola intersects the symmetrical axis is known as the vertex of the parabola, and in this case, the vertex is (0,0).
Focal Chord: The chord that passes through the focus of the parabola is called the focal chord. The focal chord always cuts the parabola at two points.
Latus Rectum: Latus rectum is a focal chord that is parallel to the directrix while it is perpendicular to the symmetrical axis of the parabola. The length of the Latus rectum for all the standard forms of the parabola is taken as “
Eccentricity: The eccentricity of a parabola is always equal to 1. It is the ratio of the distance of a point on a parabola from its focus to the distance of the point perpendicular to the directrix of the parabola.
We have discussed the features of the parabola. Now, let us look at some of the formulas for some of these features, as the formulas are essential to represent a given equation in a graphical form.
Vertex of a parabola
Directrix
Letus Rectum
Focus
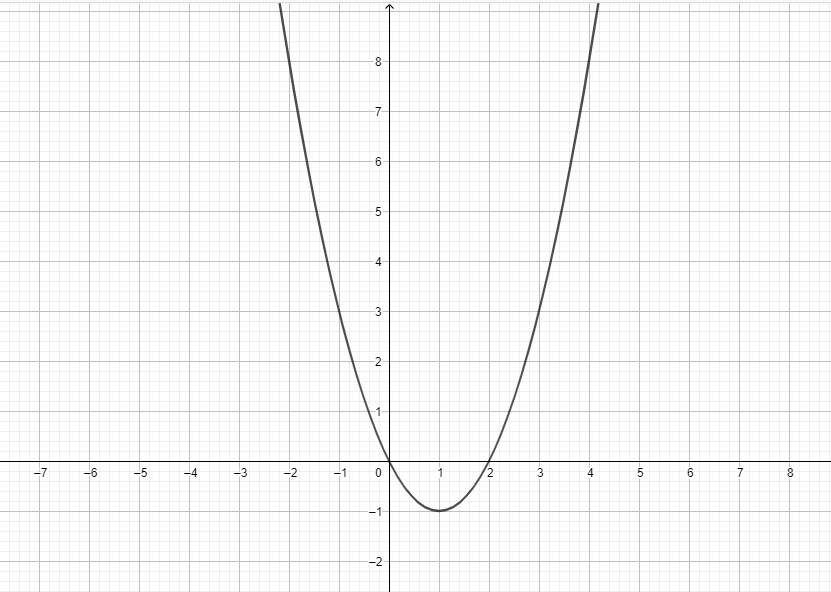
How to Graph y = x^2
The graph of the
- The first step is to write the equation in the form
- The next step is to determine the axis of symmetry. We know that the symmetrical axis is perpendicular to the directrix, and it cuts/divides the parabola in half. It is calculated as
- The next step is to determine the vertex. We know that vertex is the point of intersection on the perpendicular symmetrical axis. In this case, the value of
- In the next step, we find out different points on the graph of
| x | y | x^2 | (x,y) |
We can represent the parabola
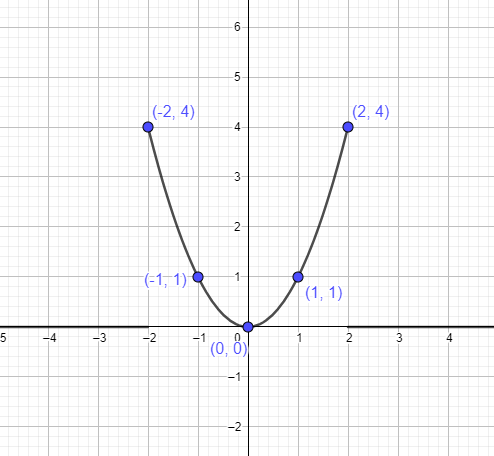
Example 1: Is y =x^2 a linear function?
Solution:
No, the linear equations have a degree of
Example 2: We know the equation y =x^2 is a parabola. What does the equation
Solution:
The equation
If we are given the function
If we are given the function
Practice Questions:
- Determine the value of
- Draw the graph for
- Does the function
- Draw the graph for
Answer Key:
1)
The value of
At
at
y
at
at
2)
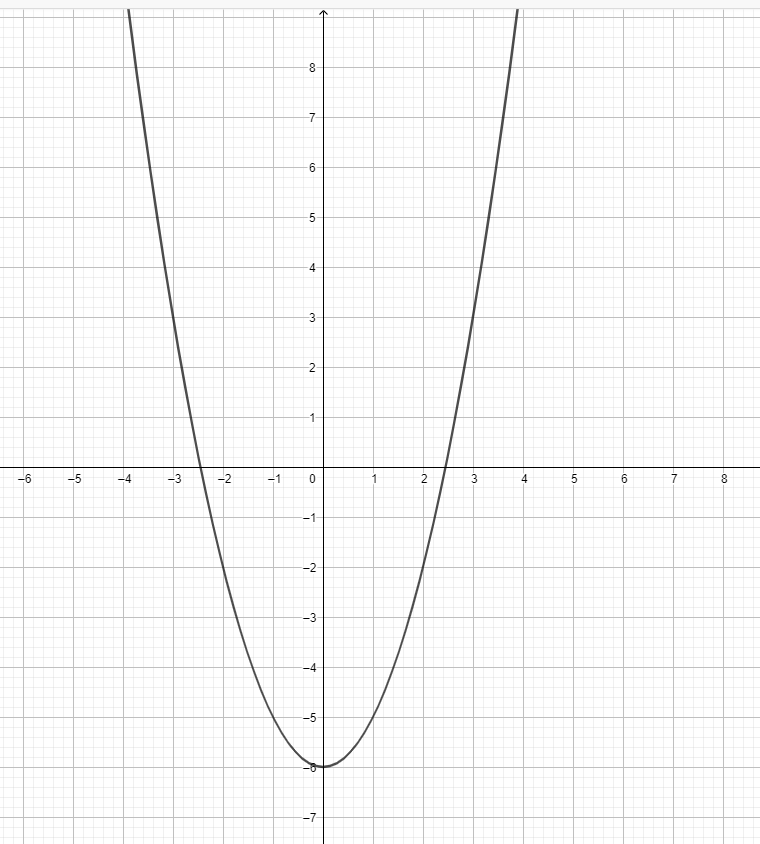
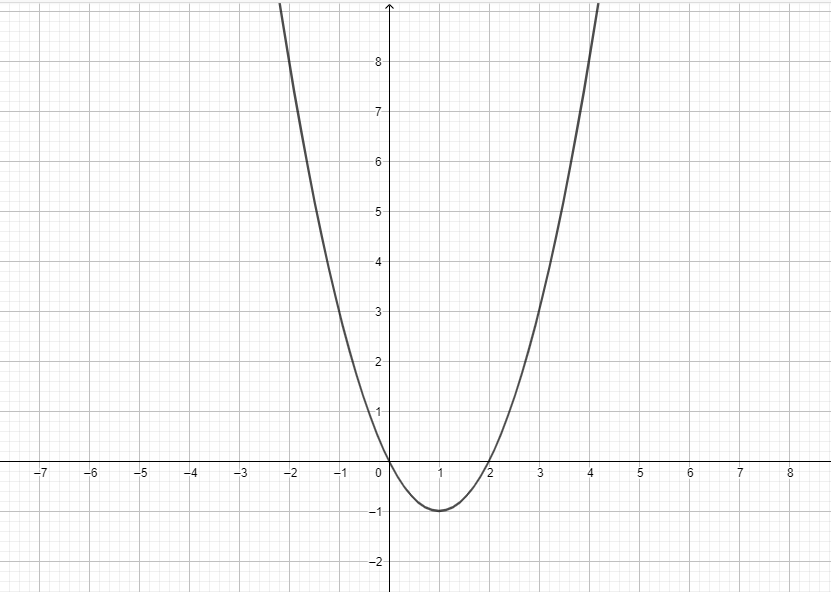
3)
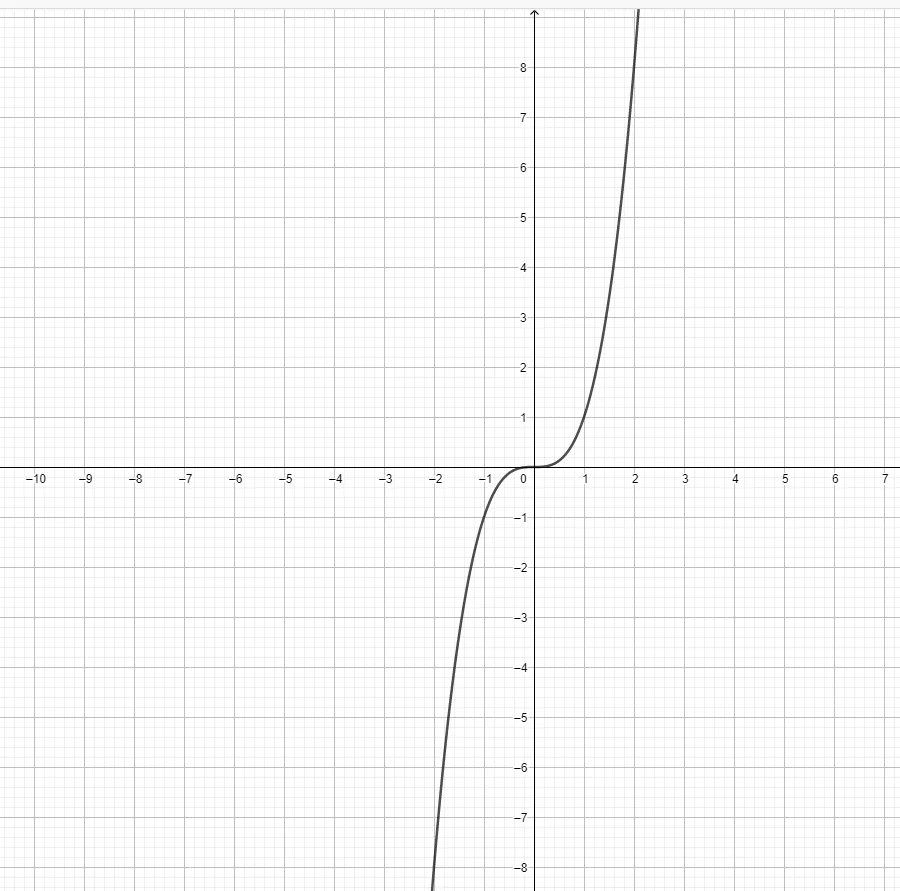
4)