JUMP TO TOPIC

Expert Answer:
The greatest integer function is not differentiable on any real value of x because this function is discontinuous on all the integer values, and it has no or zero slopes on every other value. We can see the discontinuity in Figure 1.
Let f(x) is a floor function which is represented in Figure 1. We can see from the figure that the greatest integer function is discontinuous on every integer function, thus its derivative does not exist at those points.
\[ f(x) = \llcorner x \lrcorner , [-2, 2] \]
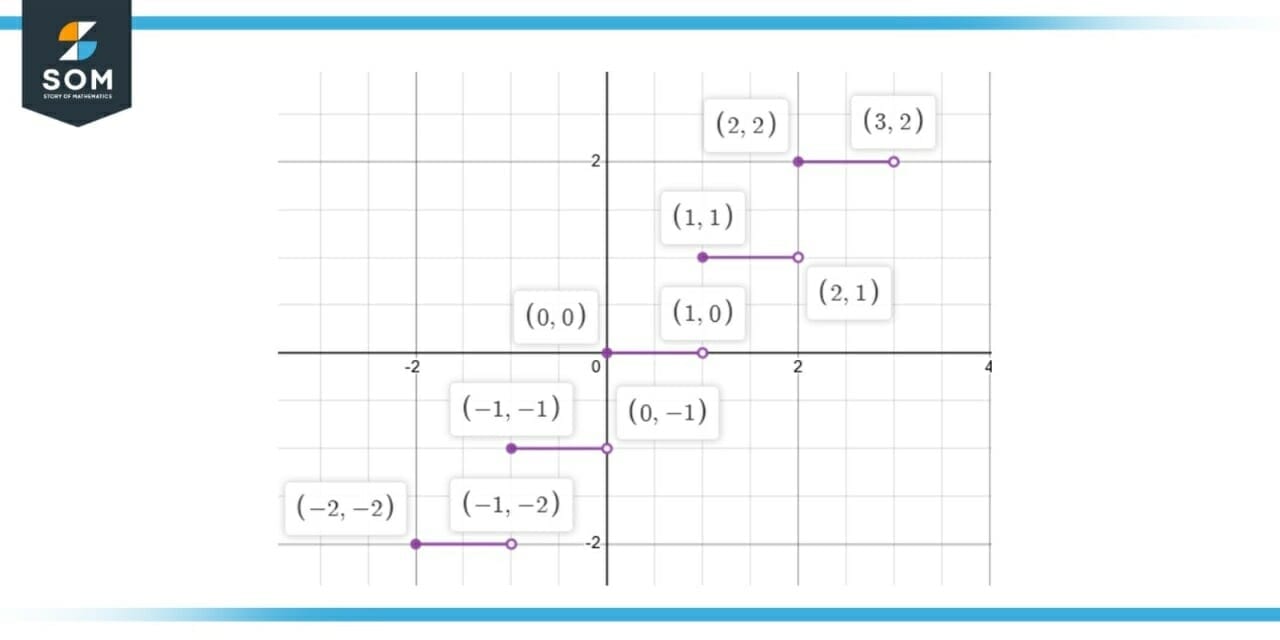
Figure-1 : Floor Function f(x)
This question aims to find the points where the derivative of the greatest integer function or more commonly known as the floor function does not exist.
The greatest integer function is the function that returns the nearest integer value to a given real number. It is also known as floor function and is represented by $f(x) = \llcorner x \lrcorner$. This means that it returns the integer lower than the given real number. The derivative gives the rate of change of a function with respect to a variable. The derivative gives the slope of the tangent line at that point and the slope represents the steepness of the line.
As shown in Figure 1, the floor function is discontinuous on all the integer values and its slope is zero between two integer values, which results in differentiation to be $0$. When we differentiate the greatest integer function, we get a horizontal line on $x-axis$ with discontinuity on all the integer values of $x$, which is represented in Figure 2.
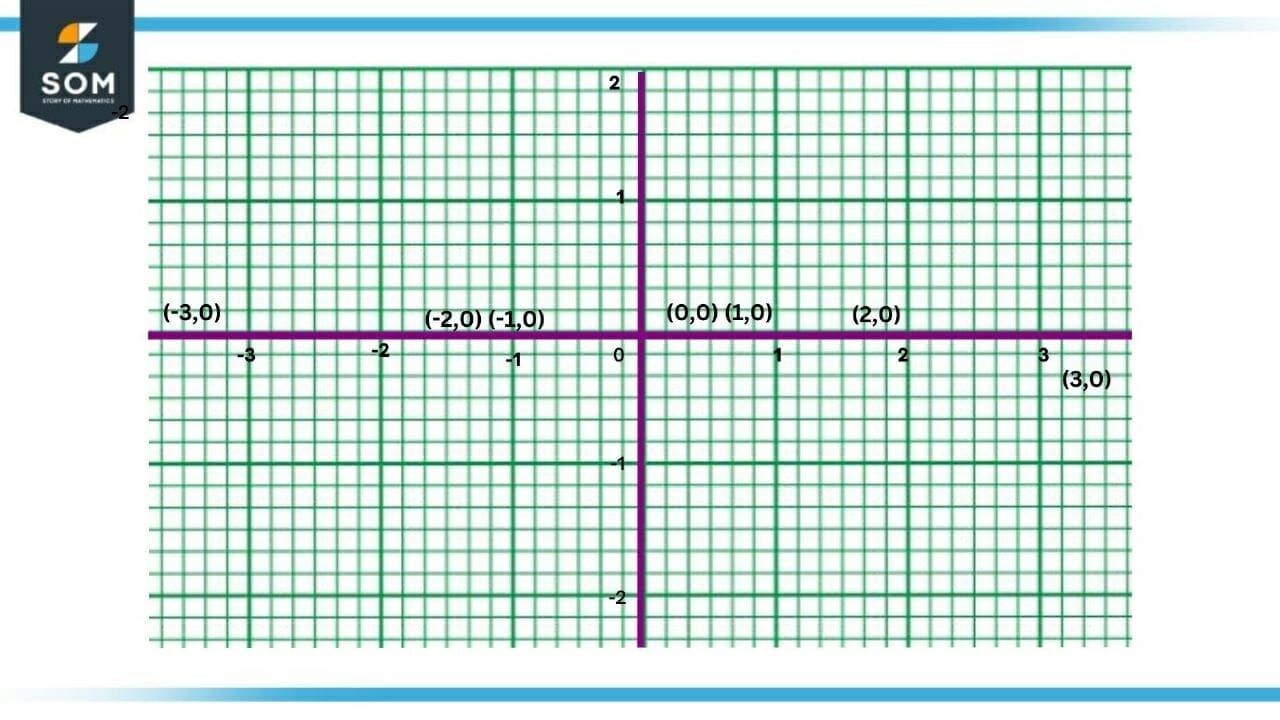
Figure-2 : Slope of Floor Function
Numerical Results:
\[ f(x) = \llcorner x \lrcorner \]
Then derivative of $f(x)$ would be:
\[ f \prime (x) = \begin{cases} \text{Discontinuous} & \text{when $’x’$ is an integer} \\ \text{0} & \text{otherwise} \end{cases} \]
Figure 2 shows the derivative of the greatest integer function which does not exist on integer values and it is zero on every other real value of $x$.
Example:
Prove that the greatest integer function $f(x)=\llcorner x \lrcorner, 0<x<3$ is not differentiable at $x=1$.
We need to recall the concept of derivative by definition. It states that the limit of the slope of the secant line from a point $c$ to $c+h$ as $h$ approaches zero. The function is said to be differentiable at $c$ if the limit of the function before and after $c$ is equal and not zero. Figure 3 shows the graph of the greatest integer function for the values of $x$ from $0$ to $3$.
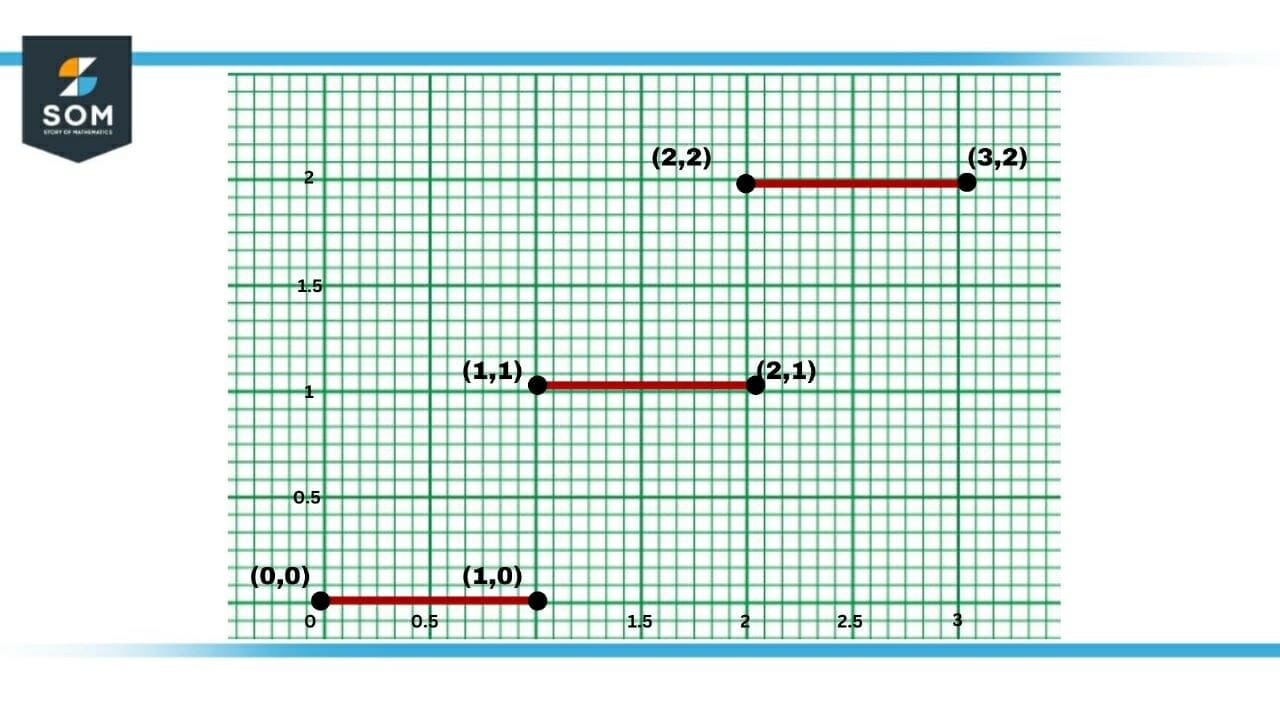
Figure-3 : Greatest Integer Function
Given in this problem that $c=1$.
$f(x)$ is differentiable at $x=c=1$, if:
\[ \lim_{h \rightarrow 0} \dfrac{f(x + h) – f(x)}{h} \]
Substituting the value of $x$ in the above equation,
\[ \lim_{h \rightarrow 0} \dfrac{f(1 + h) – f(1)}{h} \]
\[ \lim_{h \rightarrow 0} \dfrac{(1 + h) – (1)}{h} \]
As $(1 + h) < 1$, then $(1 + h) = 0$ and $(1 + h) > 1$, then $(1 + h) = 1$.
For $1 + h < 1$,
\[ \lim_{h \rightarrow 0} \dfrac{0 – 1}{h} \]
\[ \lim_{h \rightarrow 0} \dfrac{- 1}{h} \]
As h approaches zero, function approaches infinity, where the slope does not exist and it is not differentiable.
For $1 + h > 1$,
\[ \lim_{h \rightarrow 0} \dfrac{1 – 1}{h} \]
\[ \lim_{h \rightarrow 0} \dfrac{0}{h} = 0 \]
The slope of the function at this point is zero, so the function is not differentiable at $x=1$. Figure 4 shows the graph of the derivative of the greatest integer function at $x=1$, which does not exist at $x=1$ and is zero before and after that value.
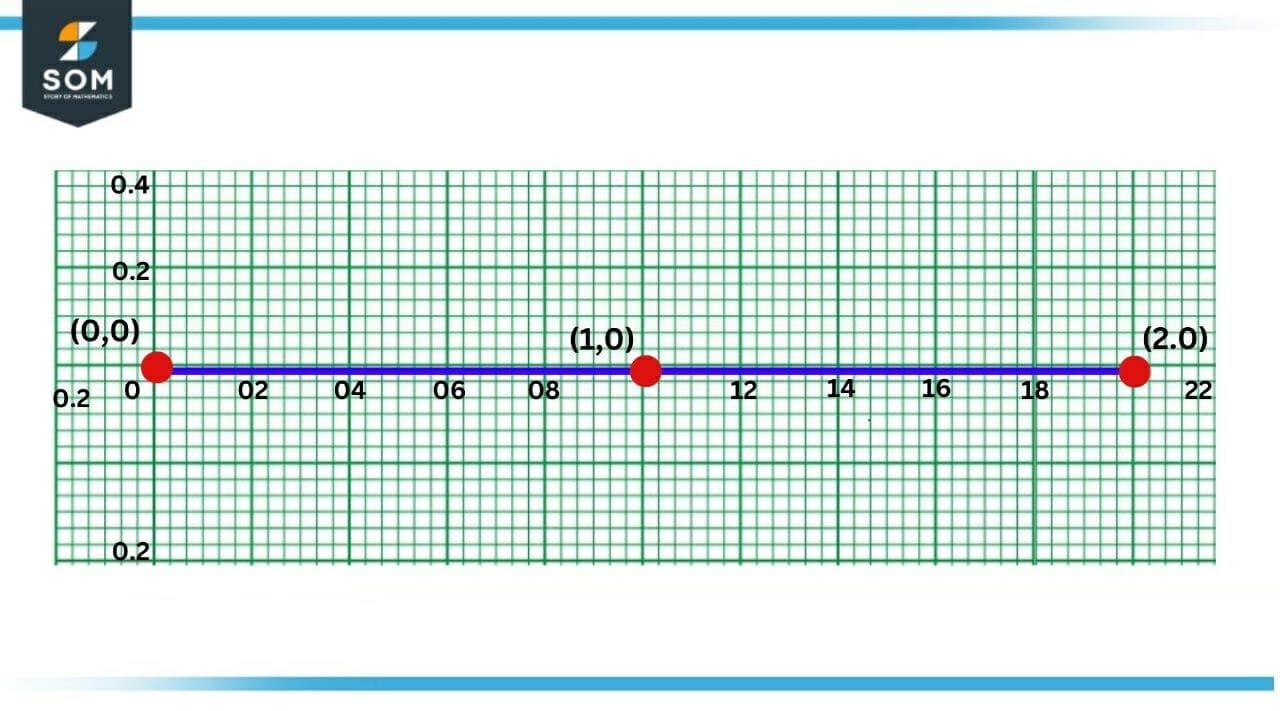
Figur-4 : Derivative of Greatest Integer Function
Images/Mathematical drawings are created with Geogebra.
