JUMP TO TOPIC
What is 2i? It is an imaginary number because 2i has the form $bi$, where $b$ is a real number, and $i$ is the imaginary unit. These numbers give a value for the square root of negative numbers. Note that the square root of a negative number does not exist in the real line. Let us learn more about the world of complex and imaginary numbers and know what they represent and how we use them in mathematics.
Why 2i Is Imaginary?
The number 2i is an imaginary number because it has the form $bi$, where $b$ is real and $i$ is the imaginary unit. Take note that $i$ is equal to the square root of $-1$.
We consider a number as imaginary if it can be expressed as a product of a real number and $i$. They do not exist in the real line, instead, they are found in the complex number system. Since $i$ is the imaginary unit whose square is $-1$, then if we take the square of an imaginary number, we will always get a negative number. Thus, the square of $2i$ is $-2$.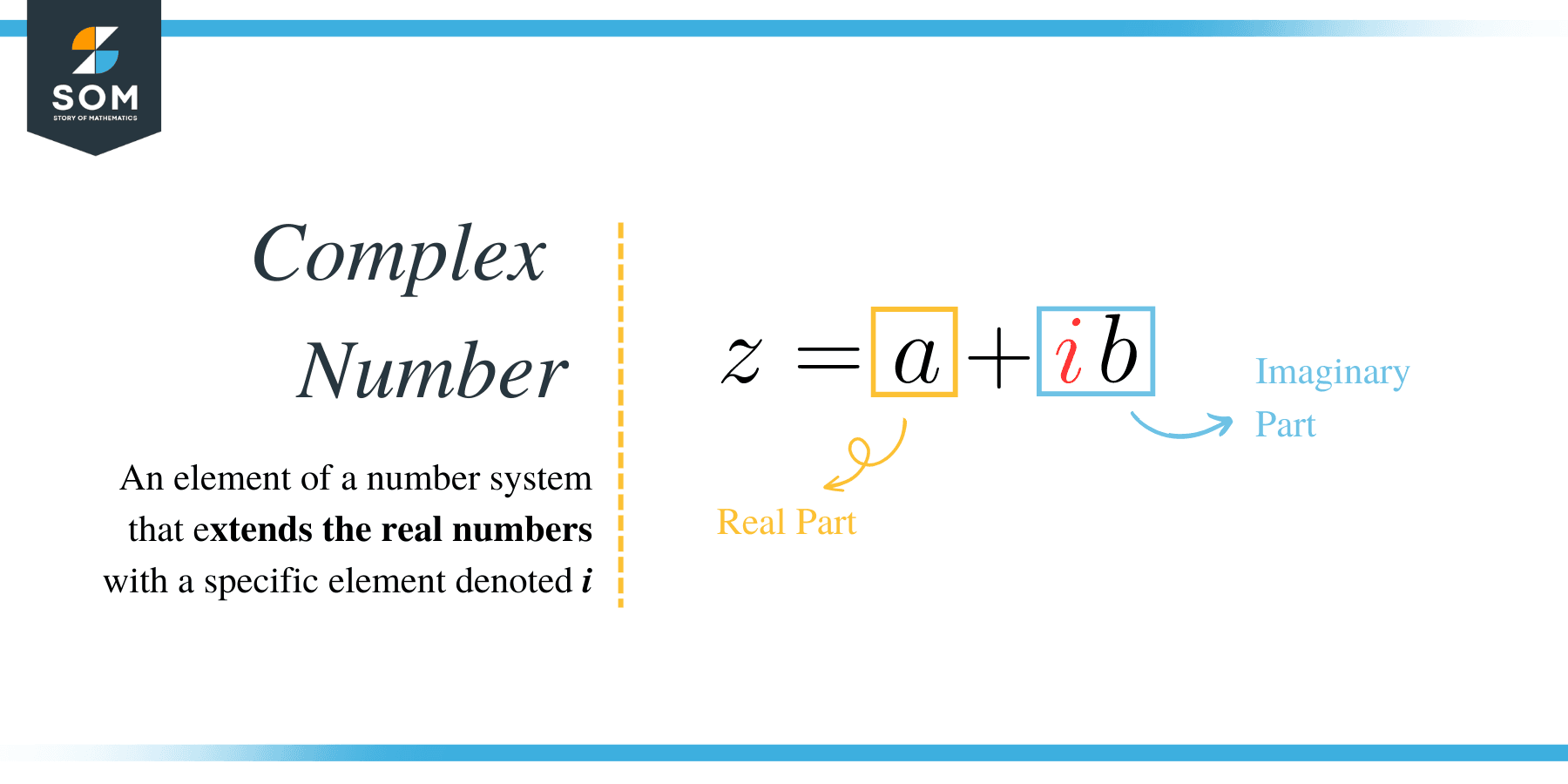
Example
Check the detailed example below:
- $\pi i$ is imaginary. It is of the form $bi$ where $b=\pi$ and $\pi$ is in the real line.
- $-i$ is also imaginary because it is a product of $-1$, which is real, and $i$. Moreover, the square of $-i$ is $-1$.
- Another number that is imaginary is $\dfrac{i}{2}$. It is the product of $\dfrac{1}{2}$ and $i$.
Even if they are termed as “imaginary”, these numbers are real in the sense that they exist in mathematics and are defined for a purpose.
What Is 2i in Math?
The number $2i$ in math is the imaginary solution to the equation $x^2+4=0$. How is that? Let’s learn more in the following discussion.
In the real number system, we are stuck when we need to find the solutions for $x^2+1=0$. The solution for this is $x=\pm\sqrt{-1}$, which does not exist in the real line because the roots of any negative number in the real system do not exist. Thus, this is equivalently saying that the equation does not have a real solution.
However, if we are going to expand the set where we will get our solution, we might get a solution for the equation. If we are going to extend it to the complex number system, the equation has a solution. This means that we can derive a solution for this equation that is not real. Consequently, the solutions that we have are imaginary solutions since they only exist in the imaginary line.
In general, imaginary numbers are imaginary solutions to equations of $x^2 +a=0$, where $a$ is a positive number. Moreover, the solutions to this equation are $x= \pm\sqrt{a}i$.
Example
- The imaginary solutions for the equation $x^2+9=0$ are $3i$ and $-3i$.
- The equation $x^2+25=0$ has imaginary solutions $5i$ and $-5i$.
What Is the Value of 2i?
The value of $2i$ in the complex system is $2$. More precisely, to know the value of any number, either real or complex, what we really are trying to find is its absolute value. The absolute value of a number $x$ is denoted by $|x|$, which is read as, “the absolute value of $x$”.
If a number is real, the absolute value of the number refers to its distance of the number from zero. Thus, the absolute value of $x$, where $x$ is real, is itself if $x$ is positive or zero, and its absolute value is $-x$ if $x$ is negative.
For the complex case, note that if $z$ is complex and $z=x+iy$, where $x$ is the real part and $y$ is the imaginary part, then we can think of $z$ as a point with coordinates $(x, y)$. We can interpret the absolute value of numbers in the complex system, as the distance from the origin or the number zero. Note that $0=0+0i$, which makes sense that the origin $(0, 0)$ is the complex zero.
The absolute value for any complex $z$, with $z=x+iy$, is the root of the sum of the squares of the real and imaginary part of $z$. In formula, it is given by $|z| = \sqrt{x^2+y^2}$.
So, let’s verify that the value of 2i simplified is $2$. First, we expand $2i$ to determine its real and imaginary parts. Note that $2i =0 + 2i$. This means that $2i$ has real part $0$ and the imaginary part is $2$. So we have, $|2i|=\sqrt{0^2+2^2}=\sqrt{0+4}=\sqrt{4}=2$.
Example
Check the example for a better understanding:
- The complex $1-2i$ has real part $1$ and imaginary part $-2$. Thus, the absolute value of $1-2i$ is $\sqrt{5}$ because $|1-2i|=\sqrt{(1)^2+(-2)^2}=\sqrt{1+4}=\sqrt{5}$.
FAQ
Is 2i a Real Number?
No, $2i$ is not an element of the real line. All numbers that are imaginary do not belong in the real system. We discussed that $2i$ is a complex solution to the equation $x^2+4=0$. However, since there is no real $x$ that can satisfy this equation, then $2i$ is not real.
What Is 2i Squared?
What Does -2i Equal in Math?
Is the Square Root of 2 an Imaginary Number?
Is Imaginary Line Part of The Complex Number System?
In general, the number system where the imaginary line can be found is the complex number system. This set contains all numbers that are imaginary, real, and the combination of these two numbers. All the numbers contained in this set are called complex numbers.
Complex numbers are composed of a real part and an imaginary part. In general, complex numbers carry the form $a+bi$, where $a$ and $b$ are real. Take note that every number, either imaginary or real, is a complex number. How is that so?
Since a complex number has the form $a+bi$, when $a=0$, then we are left with the term $bi$. That is, the resulting number is imaginary. Similarly, if we take $b=0$, then the only term left will be $a$, which is real. Thus, imaginary and real numbers are both elements of the complex system. For example, $1-2i$ is a complex number such that the real part is $1$ and the imaginary part is $-2i$.
We can always think of the complex system as an extension field of the real system to solve quadratic roots that do not have a real solution. Now that we are acquainted with the numbers in the complex system, let us take a look at what value these numbers hold and how we can use them in math.
Conclusion
The importance of complex and imaginary numbers is as much as these numbers are – they are infinite. We have covered everything you need to know in this article about the forms of imaginary and complex quantities, what value they hold, and how they are interpreted in mathematics. To keep your mind refreshed from all our discussions, let’s note some important points in this reading.
- $2i$ is a number that is referred to as imaginary because it follows the form $bi$, where $b$ is real and $i$ is the imaginary unit.
- $2i$ is the complex solution to the equation $x^2+4=0$. The other complex solution to this equation is $-2i$.
- The absolute value of $2i$ is $2$, obtained from using the formula $|z| = \sqrt{x^2+y^2}$ where $x$ is the real part and $y$ is the imaginary part of $z$.
- $2i$ is not an element of the real line, as the numbers that are imaginary do not belong in the real system.
- All numbers, either imaginary or real, are complex.
In this article, we have dissected the number $2i$. This is important because if we fully understood the value of $2i$, we can generalize it and apply it to any number in the complex system. Now that we are fairly introduced to these numbers, we are confidently armored to combat the more complex topics in complex analysis.