Volume of Rectangular Prisms – Explanation & Examples

The volume of a rectangular prism is the measure of the space the fills it. In this article, you will learn how to find a rectangular prism volume by using the volume of a rectangular prism formula. We will also discuss the volume of a spherical cylinder.

How to Find the Volume of a Rectangular Prism?

A rectangular prism is a 3-dimensional object with six rectangular faces. A rectangular prism is also referred to as a cuboid, rectangular hexahedron, right rectangular prism, or a rectangular parallelepiped.

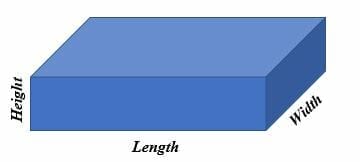
To find the volume of a rectangular prism, multiply the length, width, and height. The unit for measuring the volume of a rectangular prism is cubic units, i.e., cm³, mm³, in³, m^3, etc.

Volume of a Rectangular Prism Formula

The formula for the volume of a rectangular prism is given as:

Volume of a rectangular prism = (length x width x height) cubic units.

V = (l x w x h) cubic units

In a rectangular prism, the product of the length and the width is known as the base area. Therefore, we can also represent the volume of a rectangular prism formula as:

Volume of a rectangular prism = Base area x height

Let’s try the formula by working out a few example problems.

Example 1

The length, width, and height of a rectangular prism are 15 cm, 10 cm, and 5 cm, respectively. What is the volume of the prism?

Solution

Given, length = 15 cm,

width = 10 cm,

height = 5 cm.

By the volume of a rectangular prism, we have

Volume = l x w x h

= (15 x 10 x 5) cm³

= 750 cm³.

Example 2

The volume of a rectangular prism is 192 cm³. If the prism’s length is twice the height and width of 6 cm, find the dimensions of the rectangular prism.

Solution

Given,

Let the height be x.

Length = 2x

Width = 6 cm.

Volume = 192.

By volume of a rectangular prism,

⇒ 192 = x(2x) (6)

⇒ 192 = 12x²

On dividing both sides by 12, we get

⇒ 16 = x²

⇒ x = 4, -4

Substitute

Length = 2x ⇒ 2x 4 =8 cm

Height = x ⇒ 4 cm

Therefore, the dimensions of the rectangular prism are 8cm, 6cm, and 4 cm.

Example 3

The length and width of a rectangular aquarium are 800 mm and 350 mm. When fish is introduced in the aquarium, the water level rises by 150 mm. Find the volume of the fish.

Solution

The volume of the fish = the volume of the water displaced.

Volume of the fish = 800 x 350 x 150 mm³

= 4.2 x 10⁷ mm³

Example 4

A rectangular water tank is 80 m long, 50 m wide, and 60 m in height. If the water’s depth in the tank is 45 m, find the volume of water required to fill the tank?

Solution

To find the water volume needed to fill the tank, subtract the available water volume from the volume of water when the tank is full.

Volume of water, when the tank is full = 80 x 50 x 60

= 240,000 m³

Volume of the water available = 80 x 50 x 45

= 180,000 m³

Volume of the water required = (240,000 – 180,000) m³

= 60,000 m³

Example 5

The volume and base area of a rectangular cargo container is 778 m³ and 120 m². Find the height of the container?

Solution

Volume of a rectangular prism = base area x height

778 = 120 x height

Divide 120 on both sides.

778/120 = height

height = 6.48 m

So, the height of the container is 6.48 m.

Example 6

Small boxes of dimension 1 m x 4 m x 5 m are to be packed in a larger rectangular container of dimension 8 m x 10 m x 5 m. Find the maximum number of small boxes that can be packed in the container?

Solution

To find the number of boxes to be packed, divide the container’s volume by the volume of the box.

Volume of the container = 8 x 10 x 5

= 400 m³.

Volume of box = 1 x 4 x 5

= 20 m³

Number of boxes = 400 m³/20 m³.

= 20 boxes.

Example 7

The external dimensions of a wooden box which is open at the top is given as 12 cm long, 10 cm wide and by 5 cm height. If the walls of the box are 1 cm thick, find the volume of the box

Solution

Find the internal dimensions of the box

Length = 12 – (1 x 2)

= 10 cm

Width = 10 – (1 x 2)

= 8 cm

Height = 5 cm – 1 …… (open at the top)

= 4 cm

Volume = 10 x 8 x 4

= 320 cm³.

Example 8

What are the dimensions of a cube with the same volume as a rectangular prism with the dimensions as 8 m by 6 m by 3 m?

Solution

Volume of a rectangular prism = 8 x 6 x 3

= 144 cm³

So, a cube will also have a volume of 144 cm³

Since we know that the volume of a cube = a³

where a is the length of a cube.

144 = a³

³√ a³ = ³√144

a = 5.24

Therefore, the dimensions of the cube will be 5.24 cm by 5.24 cm by 5.24 cm.

Example 9

Calculate the volume of a solid rectangular prism whose base area is 18 in² and height is 4 in.

Solution

Volume of a rectangular prism = length x width x height

= base area x height

V= 18 x 4

= 72 in³.

Example 10

Find the base area of a rectangular prism whose volume is 625 cm³ and height is 18 cm.

Solution

Volume = base area x height

625 = base area x 18

By dividing both sides by 18, we get

Base area = 34.72 cm²