Volume of Pyramid – Explanation & Examples

A pyramid is a 3-dimensional diagram whose polygonal base is connected to the apex by triangular faces in geometry. The triangular faces of a pyramid are known as lateral faces, and the perpendicular distance from the apex (vertex) to the base of a pyramid is known as the height.

Pyramids are named after the shape of their bases. For instance, a rectangular pyramid has a rectangular base, a triangular pyramid has a triangular base, a pentagonal pyramid has a pentagonal base, etc.

How to Find the Volume of a Pyramid?

In this article, we discuss how to find the volume of pyramids with different types of bases and solve word problems involving a pyramid’s volume.

The volume of a pyramid is defined as the number of cubic units occupied by the pyramid. As stated before, the name of a pyramid is derived from the shape of its base. Therefore, the volume of a pyramid also depends on the shape of the base.

To find the pyramid’s volume, you only need the dimensions of the base and the height.

Volume of a pyramid formula

The general volume of a pyramid formula is given as:

Volume of a pyramid = 1/3 x base area x height.

V= 1/3 A_b h

Where A_b = area of the polygonal base and h = height of the pyramid.

Note: The volume of a pyramid varies slightly depending on the polygonal base.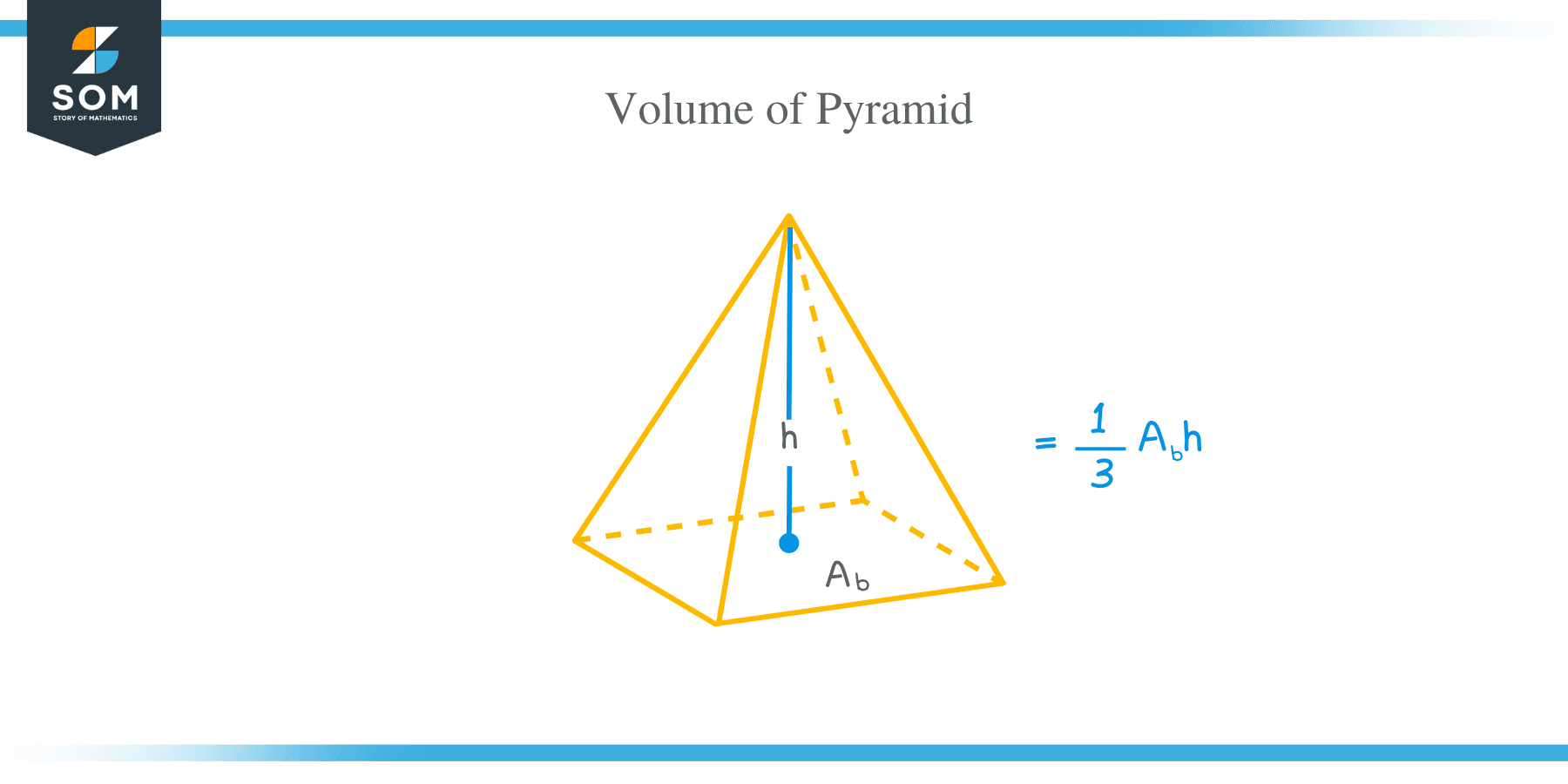

Example 1

Calculate the volume of a rectangular pyramid whose base is 8 cm by 6 cm and the height is 10 cm.

Solution

For a rectangular pyramid, the base is a rectangle.

Area of a rectangle = l x w

= 8 x 6

= 48 cm².

And by the volume of a pyramid formula, we have,

Volume of a pyramid = 1/3A_bh

= 1/3 x 48 cm² x 10 cm

= 160 cm³.

Example 2

The volume of a pyramid is 80 mm³. If the pyramid’s base is a rectangle that is 8 mm long and 6 mm wide, find the pyramid’s height.

Solution

Volume of a pyramid = 1/3A_bh

⇒ 80 = 1/3 x (8 x 6) x h

⇒ 80 = 15.9h

By dividing both sides by 15.9, we get,

h = 5

Thus, the height of the pyramid is 5 mm.

Volume of a square pyramid

To obtain the formula for the volume of a square pyramid, we substitute the base area (A_b) with the area of a square (Area of a square = a²)

Therefore, the volume of a square pyramid is given as:

Volume of a square pyramid = 1/3 x a² x h

V = 1/3 a² h

Where a = side length of the base (a square) and h = height of the pyramid.

Example 3

A square pyramid has a base length of 13 cm and a height of 20 cm. Find the volume of the pyramid.

Solution

Given:

Length of the base, a = 13 cm

height = 20 cm

Volume of a square pyramid = 1/3 a² h

By substitution, we have,

Volume = 1/3 x 13 x 13 x 20

= 1126.7 cm³

Example 4

The volume of a square pyramid is 625 cubic feet. If the height of the pyramid is 10 feet, what are the dimensions of the pyramid’s base?

Solution

Given:

Volume = 625 cubic feet.

height = 10 feet

By the volume of a square formula,

⇒ 625 = 1/3 a² h

⇒ 625 = 1/3 x a² x 10

⇒ 625 = 3.3a²

⇒ a² =187.5

⇒ a = = √187.5

a =13.7 feet

So, the dimensions of the base will be 13.7 feet by 13.7 feet.

Example 5

The base length of a square pyramid is twice the height of the pyramid. Find the dimensions of the pyramid if it has a volume of 48 cubic yards.

Solution

Let the height of the pyramid = x

the length = 3x

volume = 48 cubic yards

But, the volume of a square pyramid = 1/3 a² h

Substitute.

⇒ 48 = 1/3 (3x)² (x)

⇒ 48 = 1/3 (9x³)

⇒ 48 = 3x³

Divide both sides by 3 to get,

⇒ x³ =16

⇒ x = ³√16

x = 2.52

Therefore, the height of the pyramid = x ⇒2.53 yards,

and each side of the base is 7.56 yards

Volume of a trapezoidal pyramid

A trapezoidal pyramid is a pyramid whose base is a trapezium or a trapezoid.

Since we know, area of a trapezoid = h₁ (b₁ + b₂)/2

Where h = height of the trapezoid

b₁ and b₂ are the lengths of the two parallel sides of a trapezoid.

Given the general formula for the volume of a pyramid, we can derive the formula for the volume of a trapezoidal pyramid as:

Volume of a trapezoidal pyramid = 1/6 [h₁ (b₁ + b₂)] H

Note: When using this formula, always remember that h is the height of the trapezoidal base and H is the height of the pyramid.

Example 6

The base of a pyramid is a trapezoid with parallel sides of length 5 m and 8 m and a height of 6 m. If the pyramid has a height of 15 m, find the volume of the pyramid.

Solution

Given;

h = 6 m, H = 15 m, b₁ =5 m and b₂ = 8 m

Volume of a trapezoidal pyramid = 1/6 [h₁ (b₁ + b₂)] h

= 1/6 x 6 x 15 (5 + 8)

= 15 x 13

=195 m³.

Volume of a triangular pyramid

As we know, the area of a triangle;

Area of a triangle = 1/2 b h

Volume of a triangular pyramid = 1/3 (1/2 b h) H

Where b and h are the base length and height of the triangle. H is the height of the pyramid.

Example 7

Find the area of a triangular pyramid whose base area is 144 in² and the height is 18 in.

Solution

Given:

Base area = 144 in²

H = 18 in.

Volume of a triangular pyramid = 1/3 (1/2 b h) H

= 1/3 x 144 x 18

= 864 in³