Volume of Cones – Explanation & Examples

In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top. In simple words, a cone is a pyramid with a circular base.

Common examples of cones are ice-cream cones, traffic cones, funnels, tipi, castle turrets, temple tops, pencil tips, megaphones, Christmas trees, etc.

In this article, we will discuss how to use the volume of a cone formula to calculate the volume of a cone.

How to Find the Volume of a Cone?

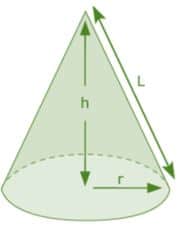
In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height (h) of a cone. A cone’s slanted lines are the length (L) of a cone along the taper curved surface. All of these parameters are mentioned in the figure above.

To find the volume of a cone, you need the following parameters:

• Radius (r) of the circular base,
• The height or the slanted height of a cone.

Like all other volumes, the volume of a cone is also expressed in cubic units.

Volume of a cone formula

The volume of a cone is equal to one-third of the base area’s product and the height. The formula for the volume is represented as:

Volume of a cone = ⅓ x πr² x h

V = ⅓ πr² h

Where V is the volume, r is the radius and h, is the height.

The slant height, radius, and height of a cone are related as;

Slant height of a cone, L = √(r²+h²) ………. (Pythagorean theorem)

Let’s gain an insight into the volume of a cone formula by working out a few example problems.

Example 1

Find the volume of the cone of radius, 5 cm, and height, 10 cm.

Solution

By the volume of a cone formula, we have,

⇒V = ⅓ πr²h

⇒V = ⅓ x 3.14 x 5 x 5 x 10

= 262 cm³

Example 2

The radius and slant height of a cone are 12 mm and 25 mm. respectively. Find the volume of the cone.

Solution

Given:

Slant height, L= 25 mm

radius, r = 12 mm

L = √ (r² + h²)

By substitution, we get,

⇒25 = √ (12² + h²)

⇒25 = √ (144 + h²)

Square both sides

⇒625 = 144 + h²

Subtract by 144 on both sides.

481 = h²

√481 = h

h = 21.9

Hence, the height of the cone is 21.9 mm.

Now, calculate the volume.

Volume = ⅓ πr²h

= ⅓ x 3.14 x 12 x 12 x 21.9

= 3300.8 mm³.

Example 3

A conical silo of radius 9 feet and height 14 feet releases cereals at its bottom at a constant rate of 20 cubic feet per minute. How long will it take for the silo to be empty?

Solution

First, find the volume of the conical silo

Volume = ⅓ x 3.14 x 9 x 9 x 14

= 1186.92 cubic feet.

To get the time take for the silo to be empty, divide the volume of the silo by the flow rate of the cereals.

= 1186.92 cubic feet/20 cubic feet per minute

= 59 minutes

Example 4

A conical storage tank has a diameter of 5 m and a height of 10 m. Find the capacity of the tank in liters.

Solution

Given, diameter = 5 m ⇒ radius = 2.5 m

Height = 10 m

Volume of a cone = ⅓ πr²h

= ⅓ x 3.14 x 2.5 x 2.5 x 10

= 65.4 m³

Since, 1000 liters = 1 m³, then

65.4 m³ = 65.4 x 1000 liters

= 65400 liters.

Example 5

A solid plastic sphere of radius 14 cm is melted down into a cone of height, 10 cm. What will be the radius of the cone?

Solution

Volume of the sphere = 4/3 πr³

= 4/3 x 3.14 x 14 x 14 x 14

= 11488.2 cm³

The cone will also have the same volume of 11488.2 cm³

Therefore,

⅓ πr²h = 11488.2 cm³

⅓ x 3.14 x r² x 10 = 11488.2 cm³

10.5r² = 11488.2 cm³

r² = 1094

r = √1094

r = 33

Therefore, the radius of the cone will be 33 cm.

Example 6

Find the volume of the cone, whose radius is 6 feet and height is 15 feet

Solution

Volume of a cone = 1/3 x 3.14 x 6 x 6 x 15

= 565.2 ft³.