Vertical Angles – Explanation & Examples

In this article, we are going to learn what vertical angles are and how to calculate them. Before we begin, let’s first familiarize ourselves with the following concepts about lines.

What are intersecting and parallel lines?

Intersecting lines are straight lines that meet or crosses each other at a certain point. The figure below shows the illustration of intersecting lines.

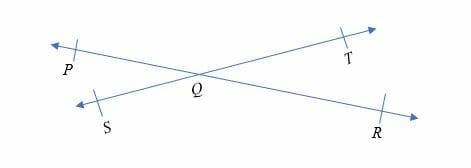
Line PQ and line ST meet at point Q. Therefore, the two lines are intersecting lines.

Parallel lines are lines that do not meet at any point in a plane.

Line AB and line CD are parallel lines because, they not intersect at any point.

What are Vertical Angles?

Vertical angles are pair angles formed when two lines intersect. Vertical angles are sometimes referred to as vertically opposite angles because the angles are opposite to each other.

Real-life settings where vertical angles are used include; railroad crossing sign, letter “X’’, open scissors pliers etc. The Egyptians used to draw two intersecting lines and always measure the vertical angles to confirm that both of them are equal.

Vertical angles are always equal to one another. In general, we can say that, 2 pairs of vertical angles are formed when two lines intersect. See the diagram below.

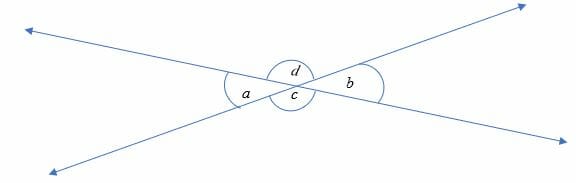
In the diagram above:

• ∠a and ∠b are vertical opposite angles. The two angles are also equal i.e. ∠a = ∠
• ∠c and ∠d make another pair of vertical angles and they are equal too.
• We can also say that the two vertical angles share a common vertex (the common endpoint of two or more lines or rays).

Proof of the Vertical Angle Theorem

We can prove in the diagram above that.

We know that angle b and angle d are supplementary angles i.e.

We also know that angle a and angle d are supplementary angles i.e.

We can re-arrange the above equations:

Comparing the two equations, we have:

Hence, proved.

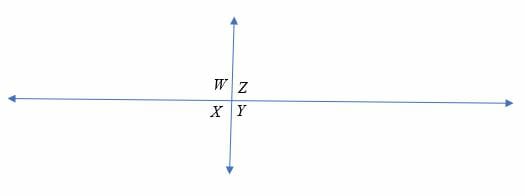
Vertical angles are supplementary angles when the lines intersect perpendicularly.

For example, ∠W and ∠ Y are vertical angles which are also supplementary angles. Similarly, ∠X and ∠Z are vertical angles which are supplementary.

How to Find Vertical Angles?

There is no specific formula for calculating vertical angles, but you can identify unknown angles by relating different angles as shown the examples below.

Example 1

Calculate the unknown angles in the following figure.

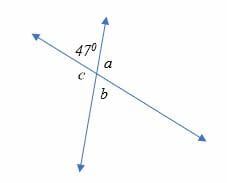
Solution

∠ 47⁰ and ∠ b are vertical angles. Therefore, ∠ b is also 47⁰ (vertical angles are congruent or equal).

∠47⁰ and ∠ a are supplementary angles. Therefore, ∠a = 180⁰ – 47⁰

⇒∠a = 133⁰

∠ a and ∠c are vertical angles. Hence, ∠ c = 133⁰

Example 2

Determine the value of θ in the diagram shown below.

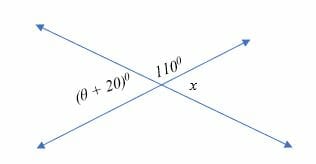
Solution

From the diagram above, ∠ (θ + 20)⁰ and ∠ x are vertical angles. Therefore,

∠ (θ + 20)⁰ = ∠ x

But 110⁰ + x = 180⁰ (supplementary angles)

x = (180 – 110)⁰

= 70⁰

Substitute x = 70⁰ in the equation;

⇒ ∠ (θ + 20)⁰ = ∠ 70⁰

⇒ θ = 70⁰ – 20⁰ = 50⁰

Therefore, the value of θ is 50 degrees.

Example 3

Calculate the value of angle y in the figure shown below.

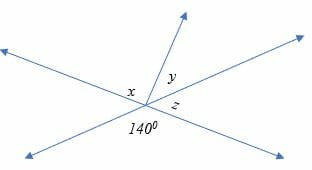
Solution

140⁰ + z = 180⁰

z = 180⁰ – 140⁰

z = 40⁰

But (x + y) + z = 180⁰

(x + y) + 40⁰ = 180⁰

x + y = 140⁰

90⁰ + y = 140⁰

y = 50⁰

Example 4

If 100⁰ and (3x + 7) ° are vertical angles, find the value of x.

Solution

Vertical angles are equal, therefore;

(3x + 7)⁰ = 100 ⁰

3x = 100 – 7

3x = 93

x = 31⁰

Hence, the value of x is 31 degrees.

Applications of Vertical Angles (h3)

Vertical angles have many applications that we see or experience in our daily lives.

• The roller coasters are being set on a certain angle for proper operation. These angles are so important that if they displaced a degree above or below, there would be a chance of an accident. The maximum vertical angle set for a roller coaster (Mumbo Jumbo, Flamingo Land’s) is 112 degrees.
• At an airshow, we experience two vapor trails that crosses each other and make vertical angles.
• Railroad crossing signs (X) placed on the roads for safety of vehicles.
• A kite, where two wooden sticks crosses and hold the kite.
• The dartboard has 10 pairs of vertical angles, where the bull’s eye is a virtual vertex.