
In the beautifully interconnected realm of mathematics, the transverse axis offers a compelling thread that weaves together multiple disciplines, from geometry to calculus. As we explore this crucial concept, its underpinning role in the integrals world cannot be overstated.
In this article, we spotlight the transverse axis, dissecting its unique position in the mathematical landscape and, specifically, its influence on the computation of integrals.
Emphasizing the importance of understanding this axis, we navigate through its defining aspects, clarifying how it shapes the landscape of numerical analysis and, ultimately, the calculation of integral values.
Definition of Transverse Axis
The transverse axis is a concept stemming primarily from geometry and is often referred to in the context of conic sections (ellipses, hyperbolas, etc.). It defines the longest diameter of an ellipse or hyperbola, going through the foci. In integrals, the transverse axis can refer to the axis along which the function is integrated.
The term “transverse axis” might also denote the axis orthogonal to the main integration axis. For instance, when evaluating double or triple integrals in polar, cylindrical, or spherical coordinates, one often integrates over an angular variable while keeping the radial variable constant, or vice versa. In these cases, the transverse axis can be viewed as perpendicular to the direction of integration.
As with many mathematical concepts, the “transverse axis” definition can depend on the context and the author’s preference. Therefore, while this definition generally holds, it’s crucial to clarify its specific use within the scope of a given discussion or work.
Properties
The transverse axis is a crucial concept in the study of conic sections, especially ellipses, and hyperbolas. Here are some key properties of the transverse axis:
Orientation
The transverse axis can be horizontal or vertical and is not limited to one orientation. Whether the major axis is parallel to the x-axis or y-axis determines how an ellipse or hyperbola’s transverse axis is oriented.
Length
The separation between the ellipse’s two furthest points, or its vertices, determines the length of its transverse axis. This length is also known as the major axis length. For a hyperbola, the transverse axis length is the distance between the two vertices of the hyperbola.
Position of Foci
The foci lie on the transverse axis in both ellipses and hyperbolas. The sum of the distances from each point on an ellipse to the two foci is determined by the length of the transverse axis, which is a constant. The distance between any point on a hyperbola and its two foci is always different from zero and equal to the transverse axis length.
Center
The center of an ellipse and a hyperbola lie on the transverse axis and is equidistant from the foci.
Eccentricity
The focal points along the transverse axis can be used to calculate the eccentricity of an ellipse or hyperbola, which measures its “flatness” or “openness.”
A “transverse axis” in integral calculus is orthogonal to the main path of integration in the case of several integrals or an axis along which a function is integrated. In these situations, the properties of the transverse axis depend heavily on the particular integral or system of coordinates under consideration.
It’s important to note that while the term “transverse axis” is commonly used in conic sections, its application and properties in other mathematical contexts may vary. Always consider the particular context when applying these properties.
Applications of Transverse Axis
The transverse axis plays a significant role in various fields of study, from pure mathematics to physics and engineering. Here’s how:
Mathematics
As highlighted, the transverse axis is critical in studying conic sections—ellipses and hyperbolas. It’s also used in integral calculus, where the transverse axis often refers to the orthogonal axis to the main integration axis, particularly in multiple integrals or in polar, cylindrical, or spherical coordinates.
Physics
In physics, the transverse axis is widely utilized. For instance, in wave motion or optics, the concept of transverse waves is quite common, where the oscillations occur perpendicular (transverse) to the direction of energy transfer. The same principle applies to light waves in physics and radio waves in telecommunications. The notion of gravitational lensing, which describes the displacement of a light source caused by the bending of light, can also be explained using the transverse axis.
Engineering
In structural and mechanical engineering, the transverse axis plays a significant role in the analysis of structures. For example, in beam analysis, loads applied perpendicular to the longitudinal axis (the transverse axis) cause bending, which is critical to determining the strength and deformation characteristics of the structure.
Astronomy and Space Exploration
The orientation and trajectory of planets and other celestial bodies are often described using the transverse axis in conjunction with other axes. It is also used in calculating the orbits of these celestial bodies.
Medical Imaging
One of the common planes (axial or transverse plane) utilized in medical imaging, such as CT scans or MRIs, to create cross-sectional images of the body is the transverse axis.
Remember that the transverse axis’s function can change depending on the situation. In all these fields, the term allows us to describe and analyze phenomena in a more structured way, contributing to the richness and versatility of scientific and mathematical language.
Exercise
Example 1
Find the length of the transverse axis of the ellipse defined by the equation 4x² + y² = 4.
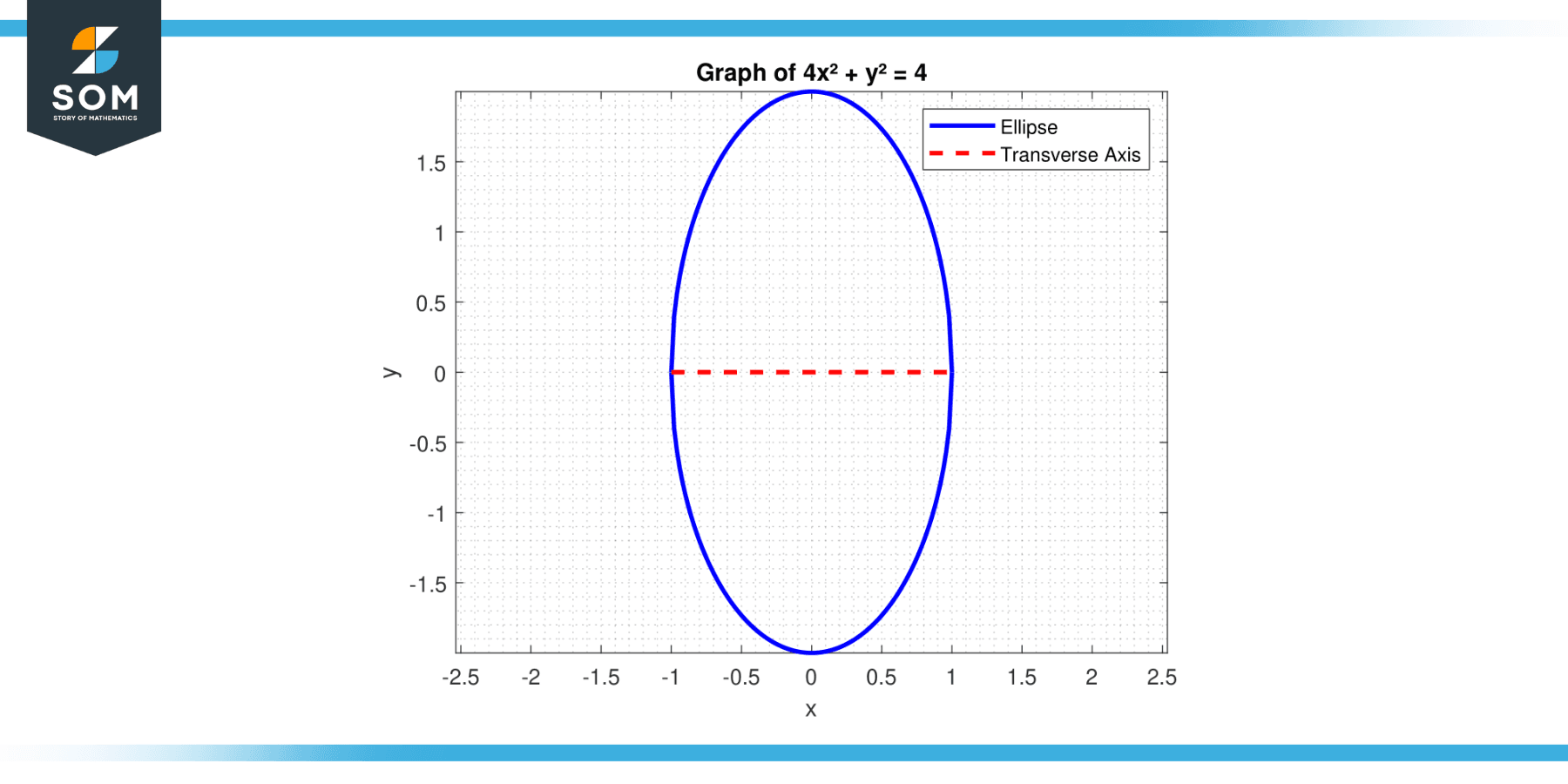
Figure-1.
Solution
The general equation for an ellipse is:
x²/a² + y²/b² = 1
To get our equation in this form, we divide by 4:
x² + y²/4 = 1
Here, a² = 1 (since a > b for an ellipse with a horizontal transverse axis), so a = 1. The length of the transverse axis is:
2 * a = 2 * 1 = 2
Example 2
Find the length of the transverse axis of the ellipse with the equation x²/16 + y²/9 = 1.
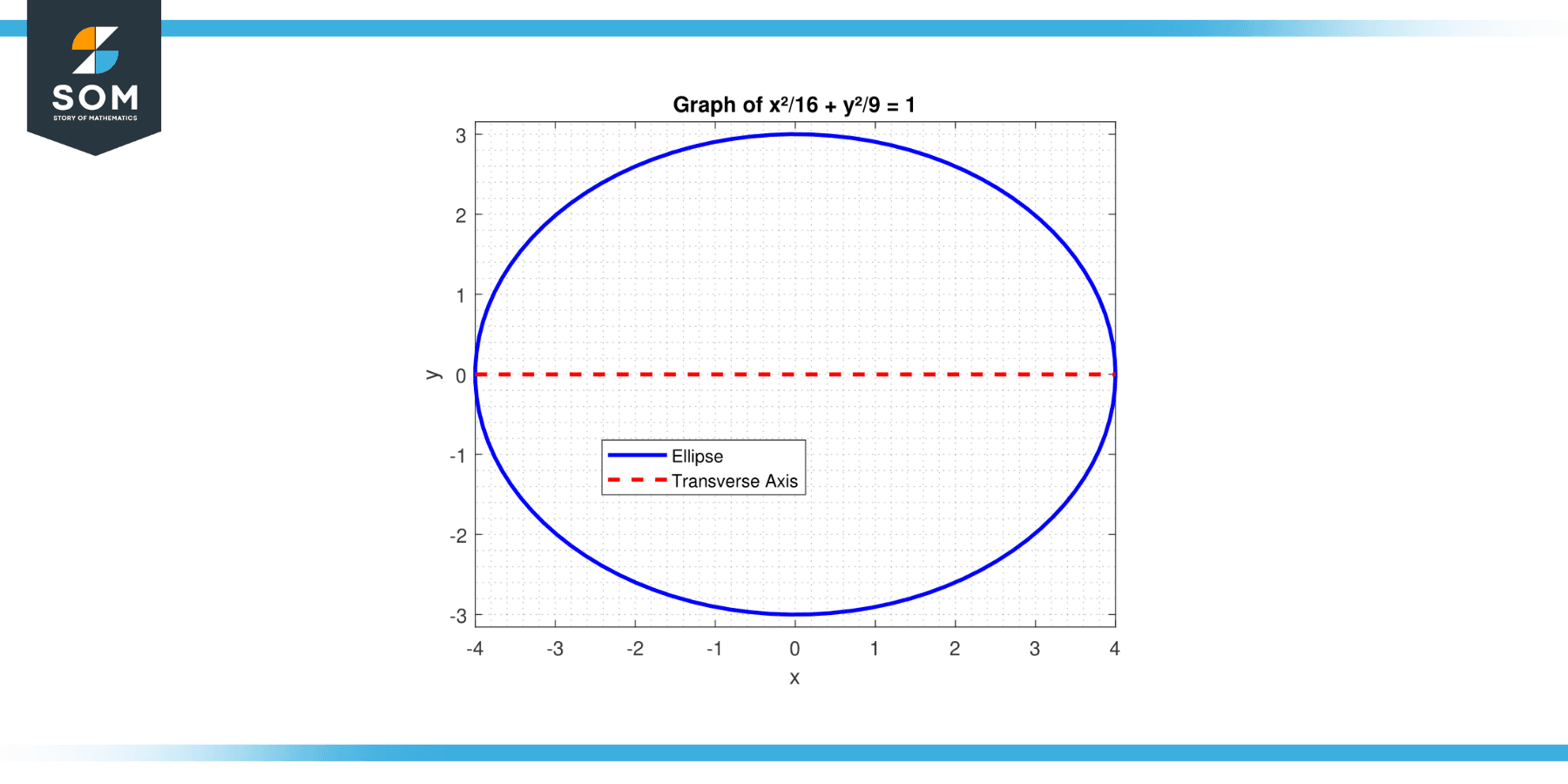
Figure-2.
Solution
Here, a² = 16 (since a > b for an ellipse with a horizontal transverse axis), so a = 4. The length of the transverse axis is:
2 * a = 2 * 4 = 8
Example 3
Find the length of the transverse axis of the hyperbola with the equation: x²/25 – y²/16 = 1.
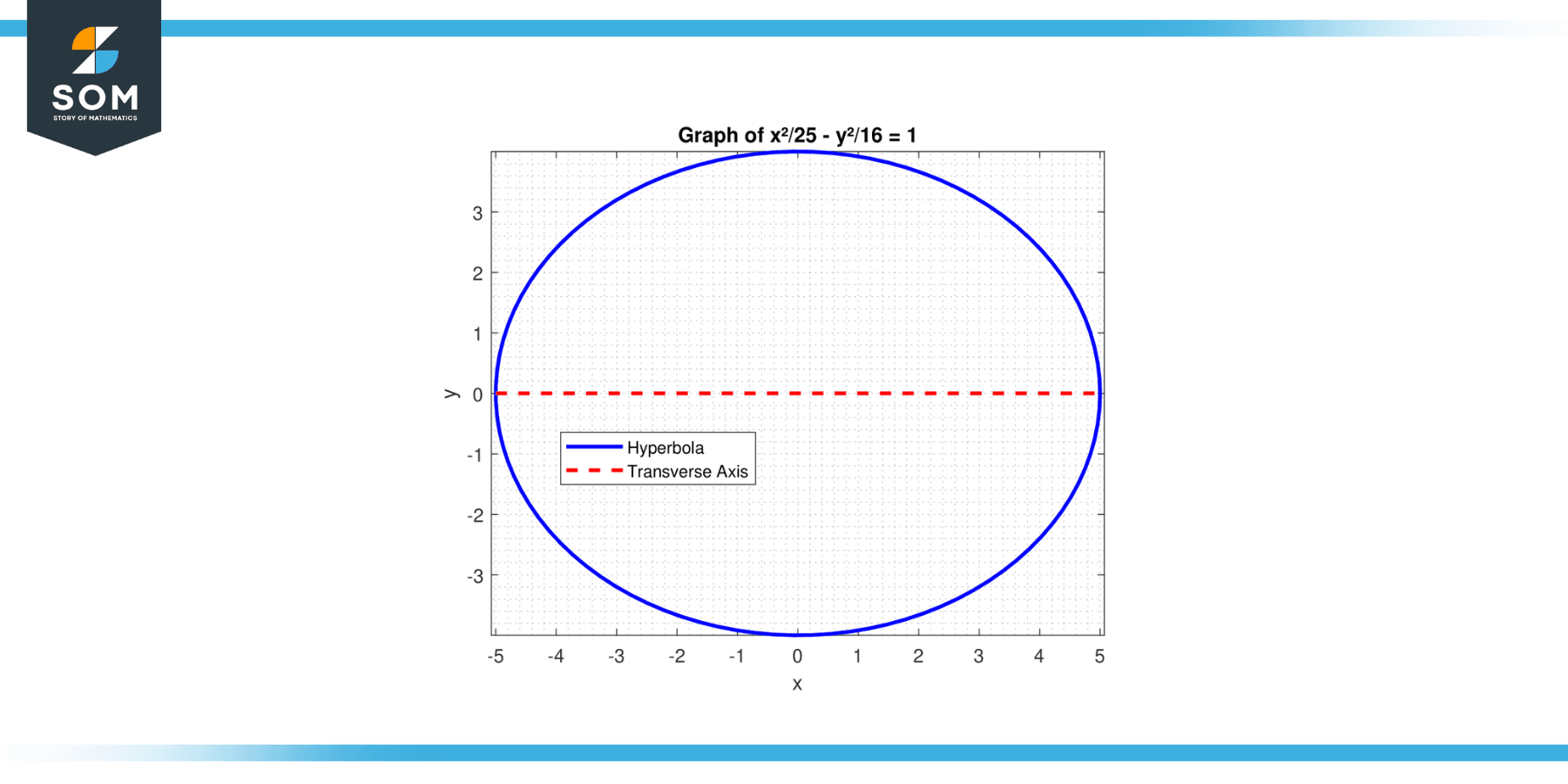
Figure-3.
Solution
For a hyperbola, a² is associated with the positive term. Here, a² = 25, so a = 5. The length of the transverse axis is:
2 * a = 2 * 5 = 10
Example 4
Find the length of the transverse axis of the hyperbola with the equation: 9x² – 4y² = 36.
Solution
Put the equation in the standard form by dividing by 36:
x²/4 – y²/9 = 1
Here, a² = 4 (since a > b for a hyperbola with a horizontal transverse axis), so a = 2. The length of the transverse axis is:
2 * a = 2 * 2 = 4
Example 5
An ellipse has a minor axis length of 8 and an eccentricity of 1/2. Find the length of the transverse (major) axis.
Solution
The eccentricity e of an ellipse is given by:
e = √(1 – (b²/a²))
where a is the semi-major axis and b is the semi-minor axis. Given b = 4 (since the minor axis length is 8, b is half of that) and e = 1/2, we solve for a:
(1/2)² = 1 – (4/a)²
Solving for a gives a = √(16/3), so the length of the transverse axis (major axis) is:
2 * a = 2 * √(16/3)
2 * a = 8 * √ (3/3)
2 * a = 8 * √(3)
Example 6
Find the vertices of the ellipse x²/9 + y²/4 = 1.
Solution
The vertices of an ellipse lie along its transverse axis. In this case, a² = 9 (since a > b for an ellipse with a horizontal transverse axis), so a = 3.
The vertices are at (a, 0) and (-a, 0), or (3, 0) and (-3, 0).
Example 7
Find the vertices of the hyperbola: 16x² – 9y² = 144.
Solution
Put the equation in standard form by dividing by 144:
x²/9 – y²/16 = 1
Here, a² = 9 (since a > b for a hyperbola with a horizontal transverse axis), so a = 3.
The vertices are at (a, 0) and (-a, 0), or (3, 0) and (-3, 0).
Example 8
An ellipse has foci at (±5, 0) and a transverse axis length 12. Find the equation of the ellipse.
Solution
For an ellipse, the distance between the foci is 2ae, where a is the semi-major axis, and e is the eccentricity.
Given 2 * a * e = 10, we find:
a = 12/2
a = 6
Also, c = a * e = 5, so we get:
e = c/a
e = 5/6
Then we find:
b = a * √(1 – e²)
b= 6 * √(1 – (5/6)²)
b = 6 * √(1 – 25/36)
b = 6 * √(11/36)
b = 2 * √(11)
Thus, the ellipse equation is x²/a² + y²/b² = 1 or x²/36 + y²/44 = 1.
All images were created with MATLAB.
