
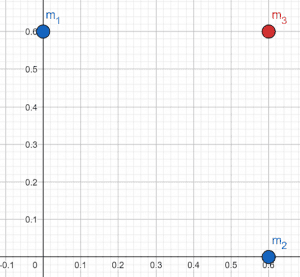
Figure (1): Arrangement of Bodies
Where, m1 = m2 = 3.0 \ kg, m3 = 4.0 \ kg
The aim of this question is to grasp the concept of Newton’s law of gravitation.
According to Newton’s law of gravitation, if two masses (say m1 and m2) are placed at some distance (say d) from each other attract each other with an equal and opposite force given by the following formula:
\[ F = G \dfrac{ m_1 \ m_2 }{ d^2 } \]
where, $ G = 6.67 \times 10^{-11} $ is a universal constant called gravitational constant.
Expert Answer
Distance $ d_1 $ between $ m_1, \ m_2 $ and origin is given by:
\[ d_1 = 0.6 \ m \]
Distance $ d_2 $ between $ m_3 $ and origin is given by:
\[ d_3 = \sqrt{ (0.6)^2 + (0.6)^2 } \ m \ = \ 0.85 \ m\]
Force $ F_1 $ acting on 0.055 kg mass (say $ m $) due to mass $ m_1 $ is given by:
\[ F_1 = G \dfrac{ m \ m_1 }{ d_1^2 } = 6.673 \times 10^{ -11 } \dfrac{ ( 0.055 )( 3 ) }{ (0.6)^2 } = 3 \times 10^{ -11 } \]
In vector form:
\[ F_1 = 3 \times 10^{ -11 } \hat{ j }\]
Force $ F_2 $ acting on 0.055 kg mass (say $ m $) due to mass $ m_2 $ is given by:
\[ F_2 = G \dfrac{ m \ m_2 }{ d_1^2 } = 6.673 \times 10^{ -11 } \dfrac{ ( 0.055 )( 3 ) }{ (0.6)^2 } = 3 \times 10^{ -11 } \]
In vector form:
\[ F_2 = 3 \times 10^{ -11 } \hat{ i }\]
Force $ F_2 $ acting on 0.055 kg mass (say $ m $) due to mass $ m_3 $ is given by:
\[ F_3 = G \dfrac{ m \ m_3 }{ d_2^2 } = 6.673 \times 10^{ -11 } \dfrac{ ( 0.055 )( 4 ) }{ (0.85)^2 } = 2.04 \times 10^{ -11 } \]
In vector form:
\[ F_3 = 3 \times 10^{ -11 } cos( 45^{ \circ} ) \hat{ i } + 3 \times 10^{ -11 } sin( 45^{ \circ} ) \hat { j }\]
\[ F_3 = 3 \times 10^{ -11 } ( 0.707 ) \hat{ i } + 3 \times 10^{ -11 } ( 0.707 ) \hat { j }\]
\[ F_3 = 2.12 \times 10^{ -11 } \hat{ i } + 2.12 \times 10^{ -11 } \hat { j }\]
Total force $ F $ acting on 0.055 kg mass (say $ m $) is given by:
\[ F = F_1 + F_2 + F_3 \]
\[ F = 3 \times 10^{ -11 } \hat{ j } + 3 \times 10^{ -11 } \hat{ i } + 2.12 \times 10^{ -11 } \hat{ i } + 2.12 \times 10^{ -11 } \hat { j } \]
\[ F = 5.12 \times 10^{ -11 } \hat{ i } + 5.12 \times 10^{ -11 } \hat{ j } \]
Magnitude of $ F $ is given by:
\[ |F| = \sqrt{ (5.12 \times 10^{ -11 })^2 + (5.12 \times 10^{ -11 })^2 } \]
\[ |F| = 7.24 \times 10^{ -11 } N\]
Direction of $ F $ is given by:
\[ F_{\theta} = tan^{-1}( \frac{ 5.12 }{ 5.12 } ) \]
\[ F_{\theta} = tan^{-1}( 1 ) \]
\[ F_{\theta} = 45^{\circ} \]
Numerical Result
\[ |F| = 7.24 \times 10^{ -11 } N\]
\[ F_{\theta} = 45^{\circ} \]
Example
Find the magnitude of the force of gravity acting between 0.055 kg and 1.0 kg masses placed at a distance of 1 m.
\[ F = G \dfrac{ m_1 \ m_2 }{ d^2 } = 6.673 \times 10^{ -11 } \dfrac{ ( 0.055 )( 1 ) }{ (1)^2 } = 0.37 \times 10^{-11} \ N \]
All the vector diagrams are constructed by using GeoGebra.
