Thales’ Theorem – Explanation & Examples

After we have gone through the Inscribed Angle Theorem, it is time to study another related theorem, which is a special case of Inscribed Angle Theorem, called Thales’ Theorem. Like Inscribed Angle Theorem, its definition is also based on diameter and angles inside a circle.

In this article, you learn:

• The Thales theorem,
• How to solve the Thales theorem; and
• How to solve the Thales theorem with only one side

What is the Thales Theorem?

The Thales theorem states that:

If three points A, B, and C lie on the circumference of a circle, whereby the line AC is the diameter of the circle, then the angle ∠ABC is a right angle (90°).

Alternatively, we can state the Thales theorem as:

The diameter of a circle always subtends a right angle to any point on the circle.

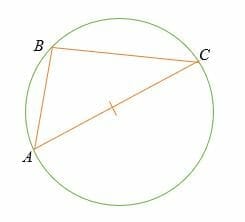
You noticed that the Thales theorem is a special case of the inscribed angle theorem (the central angle = twice the inscribed angle).

Thales theorem is attributed to Thales, a Greek mathematician and philosopher who was based in Miletus. Thales first initiated and formulated the Theoretical Study of Geometry to make astronomy a more exact science.

There are multiple ways to prove Thales Theorem. We can use geometry and algebra techniques to prove this theorem. Since this is a geometry topic, therefore, let’s see the most basic method below.

How to Solve the Thales Theorem?

• To prove the Thales theorem, draw a perpendicular bisector of ∠
• Let point M be the midpoint point of line AC.
• Also let ∠MBA = ∠BAM = β and ∠MBC =∠BCM =α
• Line AM = MB = MC = the radius of the circle.
• ΔAMB and ΔMCB are isosceles triangles.

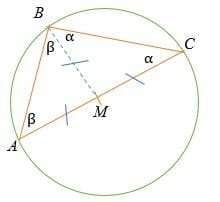
By triangle sum theorem,

∠BAC +∠ACB +∠CBA = 180°

β + β + α + α = 180°

Factor the equation.

2 β + 2 α = 180°

2 (β + α) = 180°

Divide both sides by 2.

β + α = 90°. 

Therefore, ∠ABC = 90°, hence proved

Let’s work out a few example problems involving the Thales theorem.

Example 1

Given that point O is the center of the circle shown below, find the value of x.

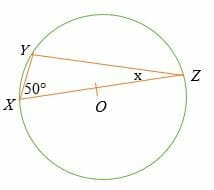
Solution

Given that the line XY is the diameter of the circle, then by Thales theorem

∠XYZ = 90°.

Sum of interior angles of a triangle = 180°

90° + 50° + x =180°

Simplify.

140° + x =180°

Subtract 140° on both sides.

x = 180° – 140°

x = 40°.

So, the value of x is 40 degrees.

Example 2

If point D is the center of the circle shown below, calculate the diameter of the circle.

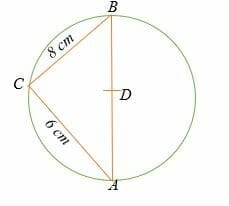
Solution

By Thales theorem, triangle ABC is a right triangle where ∠ACB = 90°.

To find the diameter of the circle, apply the Pythagorean theorem.

CB² + AC² =AB²

8² + 6² = AB²

64 + 36 = AB²

100 = AB²

AB = 10

Hence, the diameter of the circle is 10 cm

Example 3

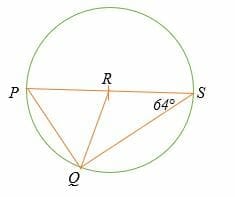
Find the measure of angle PQR in the circle shown below. Assume point R is the center of the circle.

Solution

Triangle RQS and PQR are isosceles triangles.

∠RQS =∠RSQ =64°

By Thales theorem, ∠PQS = 90°

So, ∠PQR = 90° – 64°

= 26°

Hence, the measure of angle PQR is 26°.

Example 4

Which one of the following statements is true about the definition of the Thales theorem?

A. The central angle is twice the measure of the inscribed angle

B. An angle inscribed in a half-circle will be a right angle.

C. The diameter of a circle is the longest chord.

D. The diameter of a circle is twice the length of the radius.

Solution

The correct answer is:

B. An angle inscribed in a half-circle will be a right angle.

Example 5

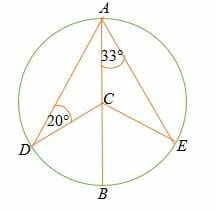
In the circle shown below, line AB is the diameter of the circle with the center C.

1. Find the measure of ∠ BCE.
2. ∠ DCA
3. ∠ ACE
4. ∠ DCB

Solution

Given triangle ACE is an isosceles triangle,

∠ CEA =∠ CAE = 33°

So, ∠ ACE =180° – (33° + 33°)

∠ ACE = 114°

But angles on a straight = 180°

Hence, ∠ BCE = 180° – 114°

= 66°

Triangle ADC is an isosceles triangle, therefore, ∠ DAC =20°

By triangle sum theorem, ∠DCA = 180° – (20° + 20°)

∠ DCA = 140°

∠ DCB = 180° – 140°

= 40°

Example 6

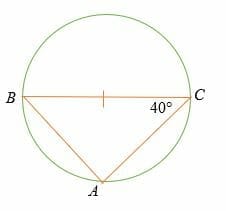
What is the measure of ∠ABC?

Solution

The Thales theorem states that BAC = 90°

And by triangle sum theorem,

∠ABC + 40° + 90° = 180°

∠ABC = 180° – 130°

= 50°

Example 7

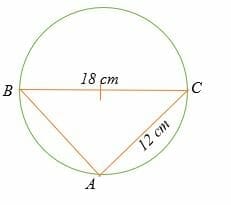
Find the length of AB in the circle shown below.

Solution

Triangle ABC is a right triangle.

Apply the Pythagorean theorem to find length AB.

AB² + 12² = 18²

AB² + 144 = 324

AB² = 324 – 144

AB² = 180

AB = 13.4

Therefore, the length of AB is 13.4 cm.

Applications of Thales Theorem

In geometry, none of the topics are without any real-life use. Therefore, Thales Theorem also has some applications:

• We can accurately draw a tangent to a circle using Thales Theorem. You can use a set square for this purpose.
• We can accurately find the center of the circle using the Thales Theorem. The tools used for this application are a set square and a sheet of paper. Firstly, you have to place the angle at the circumference—the intersections of two points with circumference state the diameter. You can repeat this using different pair of points, which will give you another diameter. The intersection of diameters will give you the center of the circle.