
The Taylor expansion of e^x is a cornerstone of calculus, allowing us to express functions as infinite series. Join us on this mathematical journey to understand the infinite power of $e^x$ through its elegant series representation.
Definition of Taylor Expansion of e^x
The Taylor expansion of $e^x$ centered at 0 is defined by:
$e^x$ = 1 + x + $(x^2/2!)$ + $(x^3/2!)$ + $(x^4/2!)$ + …
In general:
$e^x$ = $∑^{∞}_{n=0} (x^n / n!)$
This is also known as its Maclaurin series.
Generally, the Taylor expansion of a function f(x) about a point a is defined by:
f(x) = f(a) + f'(a)(x – a) + (f”(a)/2!) $(x – a)^2 + (f”'(a)/3!) $(x – a)^3$ + …
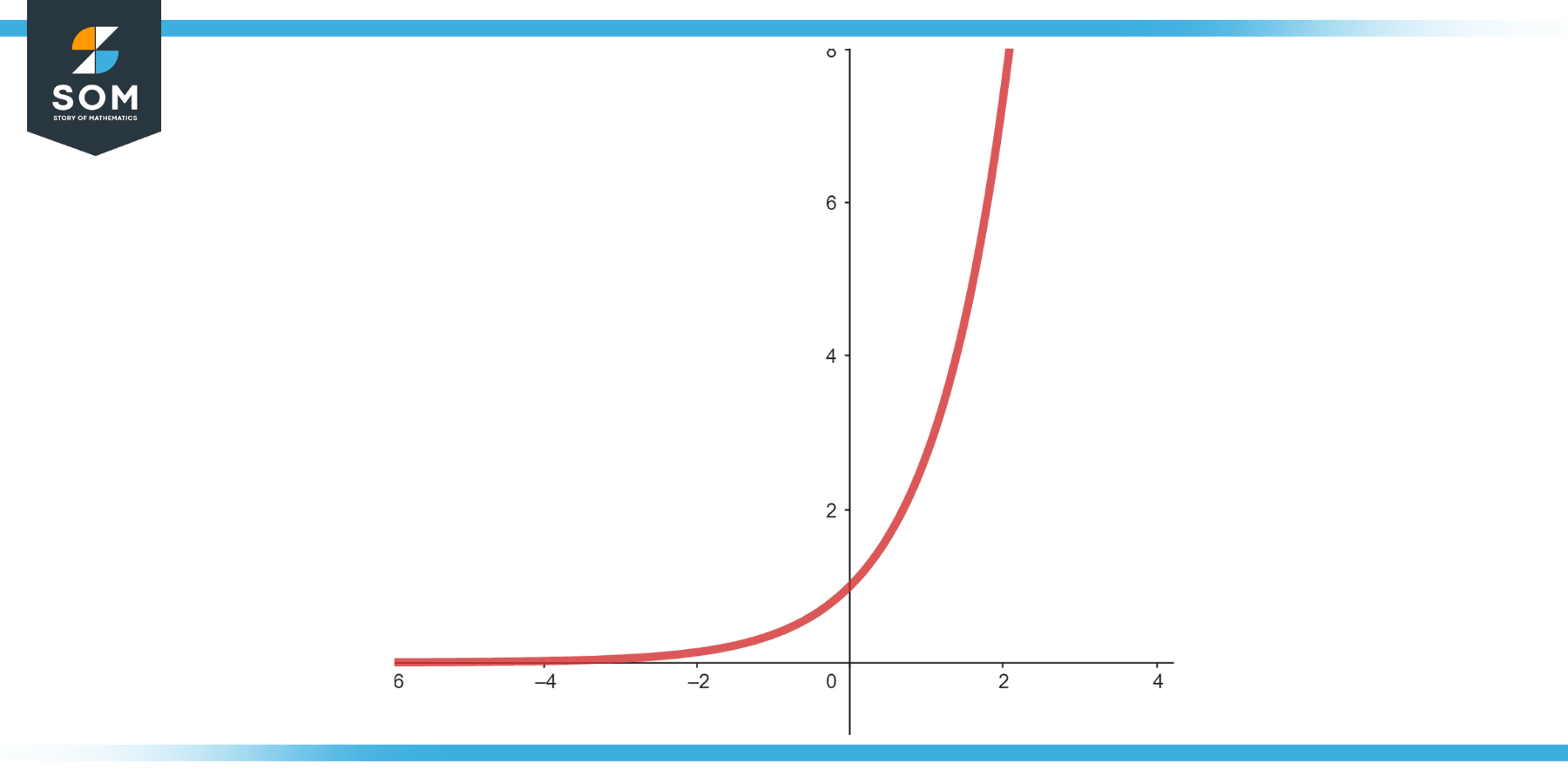
Figure-1.
Properties
The radius of Convergence
The radius of convergence for the Taylor series of $e^x$ is infinite. This means the series converges for all real values of x.
Error Bounds
If we truncate the Taylor series after a finite number of terms, we’ll have an approximation to $e^x$. The error between the actual function and its approximation is bounded by the remainder term.
For the Taylor series of $e^x$, the Lagrange form of the remainder is given by: $R_n(x)$ = $(e^c / (n+1)!) x^{(n+1)}$ where c is some number between 0 and x. Since $e^c$ is the largest value $e^x$ can take, the error is bounded by the magnitude of the next term in the series.
Super-exponential Growth
The Taylor expansion of $e^x$ gives insight into the rapid (or super-exponential) growth of this function. For large values of x, the terms in the expansion become significantly large.
Functional Properties
The Taylor series of $e^x$ reflects many properties of the exponential function itself. For instance, the property $e^{(x+y)}$ = $e^x$ * $e^y$ can be seen by multiplying two Taylor series of $e^x$ and $e^y$.
Applications in Differential Equations
The Taylor series of $e^x$ is instrumental in solving differential equations, especially linear differential equations with constant coefficients.
It helps transform differential equations into algebraic ones in the context of generating functions.
Complex Extension
The Taylor expansion of $e^x$ can be extended to complex numbers. When x = iθ (where i is the imaginary unit and θ is a real number), Euler’s formula is derived: $e^{(iθ)}$ = cos(θ) + isin(θ). This relationship bridges the exponential function with trigonometric functions through the Taylor series.
Applications
Mathematics
The Taylor series helps in solving differential equations, especially in the context of power series solutions for ordinary differential equations.
Quantum Mechanics
The exponential function, the Taylor expansion of $e^{(ix)}$ plays a role, in comprehending wavefunctions quantum states and the Schrödinger equation.
Thermodynamics
In mechanics and thermodynamics, it is common to use the Taylor series approximation to calculate partition functions and explore gas properties.
Engineering
The Laplace transform, which employs $e^{(st)}$ (a variant of $e^x$), is widely used in control systems engineering to analyze and design control systems. The Taylor series provides an understanding of how systems behave when they’re close, to a particular operating point. When analyzing circuits that involve capacitors and inductors it is common to rely on the function and its series.
Economics and Finance
Continuously compounded interest in finance is based on the exponential function. Exponential functions and their Taylor expansions are sometimes used in modeling long-term economic growth or decay.
Biology
The growth of populations, especially under unlimited resources, is often modeled using exponential growth. The series expansion aids in understanding slight variations and perturbations around steady states.
Computer Science
Some algorithms, especially those used in numerical methods, leverage the Taylor expansion of $e^x$ for fast computation and approximation of other functions. Exponential functions and their derivatives appear in various machine learning algorithms, especially in loss functions and activation functions in neural networks.
Chemistry
The exponential function, and by extension its Taylor series, plays a role in modeling the kinetics of certain chemical reactions, especially first-order reactions.
Exercise
Example 1
Approximation Using the First Few Terms
Approximate $e^{(0.5)}$ using the first four terms of the Taylor expansion of $e^x$.
Figure-2.
Solution
The Taylor series of $e^x$ around 0 is:
$e^x$ = 1 + x + $(x^2)$/2! + $(x^3)$/3! + …
For x = 0.5, using the first four terms:
$e^(0.5)$ ≈ 1 + 0.5 + $(0.5^2)$/2! + $(0.5^3)$/3!
$e^(0.5)$ ≈ 1 + 0.5 + 0.125 + 0.0208333
$e^(0.5)$ ≈ 1.6458333
Example 2
Error Estimation
Using the Taylor expansion of $e^x$, estimate the maximum error when approximating $e^{(0.2)}$ using the first three terms of the series.
Figure-3.
Solution
The Taylor series of $e^x$ is:
$e^x$ = 1 + x + $(x^2)$/2! + $(x^3)$/3! + …
The error $(e^c)/(n+1)! x^{(n+1)}$ can be estimated using the (n+1)-th term:
$(e^c)$/(n+1)! $x^{(n+1)}$
Where c is between 0 and x.
For x = 0.2 and n = 2:
$(e^c)$/(3!) $R_2$(0.2) = $(e^c)$/(3!) $e^c (0.2^3)/3$
Since $e^c$ is maximum when c = 0.2, the error is maximized at:
$(e^c)/(3!) R_2(0.2) = (e^(0.2))/(3!) e^(0.2) (0.2^3)/3$
This is the maximum error for the approximation using the first three terms.
All images were created with GeoGebra.
