Surface Area of a Sphere – Explanation & Examples
The sphere is one of the important 3d figures in geometry. To recall, a sphere is a 3-dimensional object whereby every point is equidistance (same distance) from a fixed point, known as the sphere’s center. The diameter of a sphere divides it into two equal halves, called hemispheres.
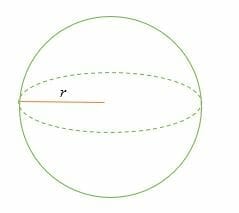
The surface area of a sphere is the measure of the region covered by the surface of a sphere.
In this article, you will learn how to find the surface area of a sphere using the surface area of a sphere formula.
How to Find the Surface Area of a Sphere?
Like a circle, the distance from the center of a sphere to the surface is known as the radius. The surface area of a sphere is four times the area of the circle with the same radius.
Surface area of a sphere formula
The surface area of a sphere formula is given as:
Surface area of a sphere = 4πr2 square units ……………. (Surface area of a sphere formula)
For a hemisphere (a half of a sphere), the surface area is given by;
Surface area of a hemisphere = ½ × surface area of sphere + area of the base (a circle)
= ½ × 4π r2 + π r2
Surface of a hemisphere = 3πr2 …………………. (Surface area of a hemisphere formula)
Where r = the radius of the given sphere.
Let’s solve a few example problems about the surface area of a sphere.
Example 1
Calculate the surface area of a sphere of radius 14 cm.
Solution
Given:
Radius, r =14 cm
By the formula,
Surface area of a sphere = 4πr2
On substitution, we get,
SA = 4 x 3.14 x 14 x 14
= 2,461.76 cm2.
Example 2
The diameter of a baseball is 18 cm. Find the surface area of the ball.
Solution
Given,
Diameter = 18 cm ⇒ radius = 18/2 = 9 cm
A baseball has a spherical shape, therefore,
The surface area = 4πr2
= 4 x 3.14 x 9 x 9
SA = 1,017.36 cm2
Example 3
The surface area of a spherical object is 379.94 m2. What is the radius of the object?
Solution
Given,
SA = 379.94 m2
But, surface area of a sphere = 4πr2
⇒ 379.94 = 4 x 3.14 x r2
⇒ 379.94 =12.56r2
Divide both sides by 12.56 and then find the square of the result
⇒ 379.94/12.56 = r2
⇒ 30.25 = r2
⇒ r = √30.25
= 5.5
Therefore, the radius of the spherical solid is 5.5 m.
Example 4
The cost of leather is $10 per square meter. Find the cost of manufacturing 1000 footballs of radius 0.12 m.
Solution
First, find the surface area of a ball
SA = 4πr2
= 4 x 3.14 x 0.12 x 0.12
= 0.181 m2
The cost of manufacturing a ball = 0.181 m2 x $10 per square meter
= $1.81
Therefore, the total cost of manufacturing 1000 balls = $1.81 x 1000
= $1,810
Example 5
The radius of the Earth is said to be 6,371 km. What is the surface area of the Earth?
Solution
The Earth is a sphere.
SA = 4πr2
= 4 x 3.14 x 6,371 x 6,371
= 5.098 x 108 km2
Example 6
Calculate the surface area of a solid hemisphere of radius 10 cm.
Solution
Given:
Radius, r = 10 cm
For a hemisphere, the surface area is given by:
SA = 3πr2
Substitute.
SA = 3 x 3.14 x 10 x 10
= 942 cm2
So, the surface area of the sphere is 942 cm2.
Example 7
The surface area of a solid hemispherical object is 150.86 ft2. What is the diameter of the hemisphere?
Solution
Given:
SA = 150.86 ft2.
Surface area of a sphere = 3πr2
⇒ 150.86 = 3 x 3.14 x r2
⇒ 150.86 = 9.42 r2
Divide both sides by 9.42 to get,
⇒ 16.014 = r2
r = √16.014
= 4
Hence, the radius is 4 ft, but the diameter is twice the radius.
So, the diameter of the hemisphere is 8 ft.
Example 8
Calculate the surface area of a sphere whose volume is 1,436.03 mm3.
Solution
Since, we already know that:
Volume of a sphere = 4/3 πr3
1,436.03 = 4/3 x 3.14 x r3
1,436.03 = 4.19 r3
Divide both sides by 4.19
r3 = 343
r = 3√343
r = 7
So, the radius of the sphere is 7 mm.
Now calculate the surface area of the sphere.
Surface area of a sphere = 4πr2
= 4 x 3.14 x 7 x 7
= 615.44 mm2.
Example 9
Calculate the surface area of a globe of radius 3.2 m
Solution
Surface area of a sphere
= 4π r2
= 4π (3.2)2
= 4 × 3.14 × 3.2 × 3.2
= 128.6 m2
Hence, the surface area of the globe is 128.6 m2.
Practice Questions
document.addEventListener("DOMContentLoaded", function(event) { if(!window.jQuery) alert("The important jQuery library is not properly loaded in your site. Your WordPress theme is probably missing the essential wp_head() call. You can switch to another theme and you will see that the plugin works fine and this notice disappears. If you are still not sure what to do you can contact us for help."); });
Loading… Loading… Loading… Loading… Loading… Loading…