JUMP TO TOPIC
Surface Area of a Solid – Explanation & Examples
 How to Find the Surface Area of a Solid?
How to Find the Surface Area of a Solid?
To determine the surface area of a solid, we take the sum of the area of all the surfaces of a 3-dimensional solid object.
This article will discuss how to find the surface area of solids, the surface area of regular solids, and irregular solids’ surface area.
Surface area of solids formula
Regular solids have definite formulas for finding their surface areas.
Common examples of regular solids include; cubes, prisms, cuboids, spheres, hemispheres, cones, and cylinders.
Surface area of regular solids
- Surface area of a solid cube:
The surface area of a solid cube = 4s2
Where s = length of the side.
- Surface area a cuboid
Surface area of a cuboid = 2lw + 2lh + 2wh
SA = 2(lw + lh + wh)
Where, l = length, w = width and h = height of the solid.
- Surface area of a solid prism:
A prism is a three-dimensional solid with two parallel and congruent polygonal bases connected by rectangular faces. The formula for the surface area for a prism depends on the shape of its base.
The general formula for the surface area of a prism = 2 × area of the base + perimeter of base × height.
SA = 2B + ph
- Surface area of a solid cylinder:
A solid cylinder is an object with two parallel and congruent circular faces connected by a curved surface.
Surface area of a cylinder = 2 × area of circle + area of a rectangle (the curved surface)
Surface area of a solid cylinder = 2πr (r + h)
- Surface area of a solid cone:
A cone is a solid with a circular base connected to a curved surface that tapers from the base to the top.
Surface area of a solid cone = Area of sector + area of a circle
SA =πrs + πr2 = πr (r + s)
Where s is the slant height of a cone and r is the radius of the circular base.
- Surface area of a solid pyramid
A pyramid can be defined as a solid with a polygonal base and triangular lateral faces. Just like a prism, a pyramid is named after the shape of its base.
The general formula for the surface area of a solid pyramid is:
SA = Base area + ½ ps
Where p = perimeter of the base and s = slant height of a pyramid.
For, a square pyramid, the surface area, SA = b2 + 2bs
Where, b = base length and s = slant height.
- Surface area of a solid sphere:
The surface area of a sphere, SA = 4 πr2
For a solid hemisphere, the surface area, SA = 3πr2
Surface area of irregular solids
An irregular object is a combination of two or more regular objects. Therefore, the surface area of an irregular solid can be calculated by adding together the regular objects’ surface areas that form it.
Let’s take a look.
Example 1
In the diagram below, the cylindrical part’s radius and height are 7 cm and 10 cm, respectively. The length, width, and height of the rectangular part are 15 cm, 8 cm, and 4 cm, respectively. Calculate the surface area irregular solid.
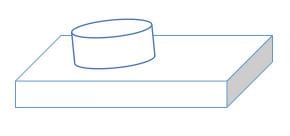
Solution
Surface area of the rectangular part = 2(lw + lh + wh)
= 2 (15 x 8 + 15 x 4 +8 x 4)
= 2 (120 + 60 + 32)
= 2 x 212
= 424 cm2.
Surface area of the cylindrical part = 2πr (r + h)
= 2 x 3.14 x 7 (7 + 10)
= 43.96 x 17
= 747.32 cm2
But, one circular face of the cylinder is hidden. Therefore, subtract its area from the surface area of the cylinder.
= 747.32 – 3.14 x 7 x 7
= 593.46 cm2
Total surface area of the irregular solid = 747.32 cm2 + 593.46 cm2
= 1,340.78 cm2.
Example 2
Given, the radius and height of the smaller cylinder are 28 cm and 20 cm, respectively. And the radius and height of the larger cylinder are 32 and 20 cm, respectively. Calculate the surface area of the solid.
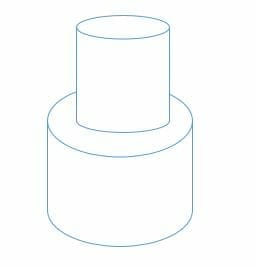
Solution
Surface area of the circular face at the top = 3.14 x 28 x 28
= 2,461.76 cm2
Curved surface area of the smaller cylinder = 3.14 x 2 x 28 x 20
= 3,516.8 cm2.
Surface area of the circular base = 3.14 x 32 x 32
=3,215.36 cm2
Area of the circular part at the top = 3,215.36 cm2 – 2,461.76 cm2
= 753.6 cm2
Curved surface area of the larger cylinder = 3.14 x 32 x 2 x 20
= 4,019.2 cm2.
Total surface area of the solid = 2,461.76 + 3,516.8 + 3,215.36 + 753.6 + 4,019.2
= 13,966.72 cm2
