Squares & Perfect Squares – Explanation & Examples

In mathematics, a square is a product of a whole number with itself. For instance, the product of a number 2 by itself is 4. In this case, 4 is termed as a perfect square.

A square of a number is denoted as n × n. Similarly, the exponential notation of the square of a number is n ², usually pronounced as “n” squared. Square numbers are usually non-negative.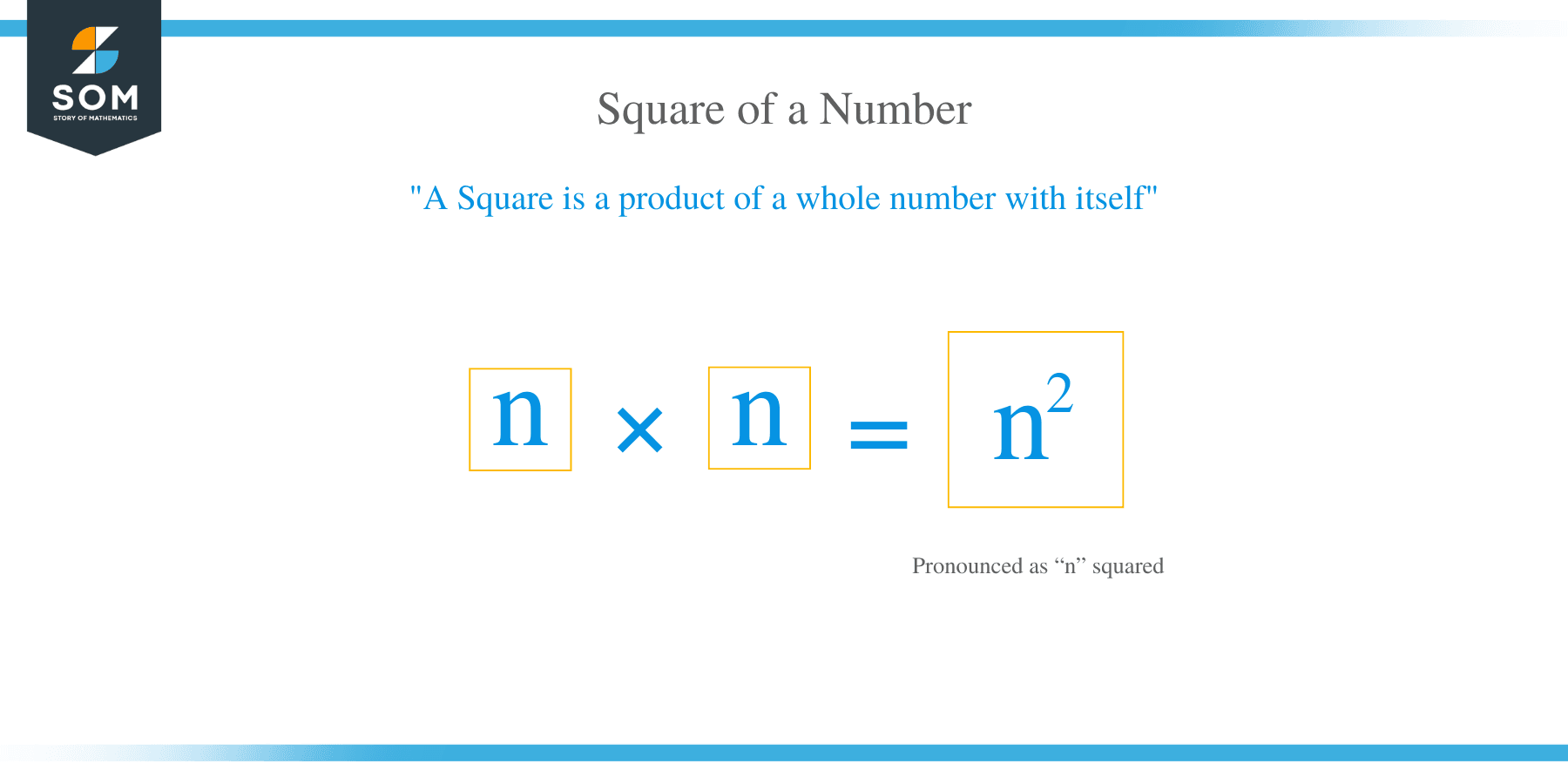

What is a Perfect Square?

A perfect square is a number that is generated by multiplying two equal integers by each other. For example, the number 9 is a perfect square because it can be expressed as a product of two equal integers: 9 = 3 x 3.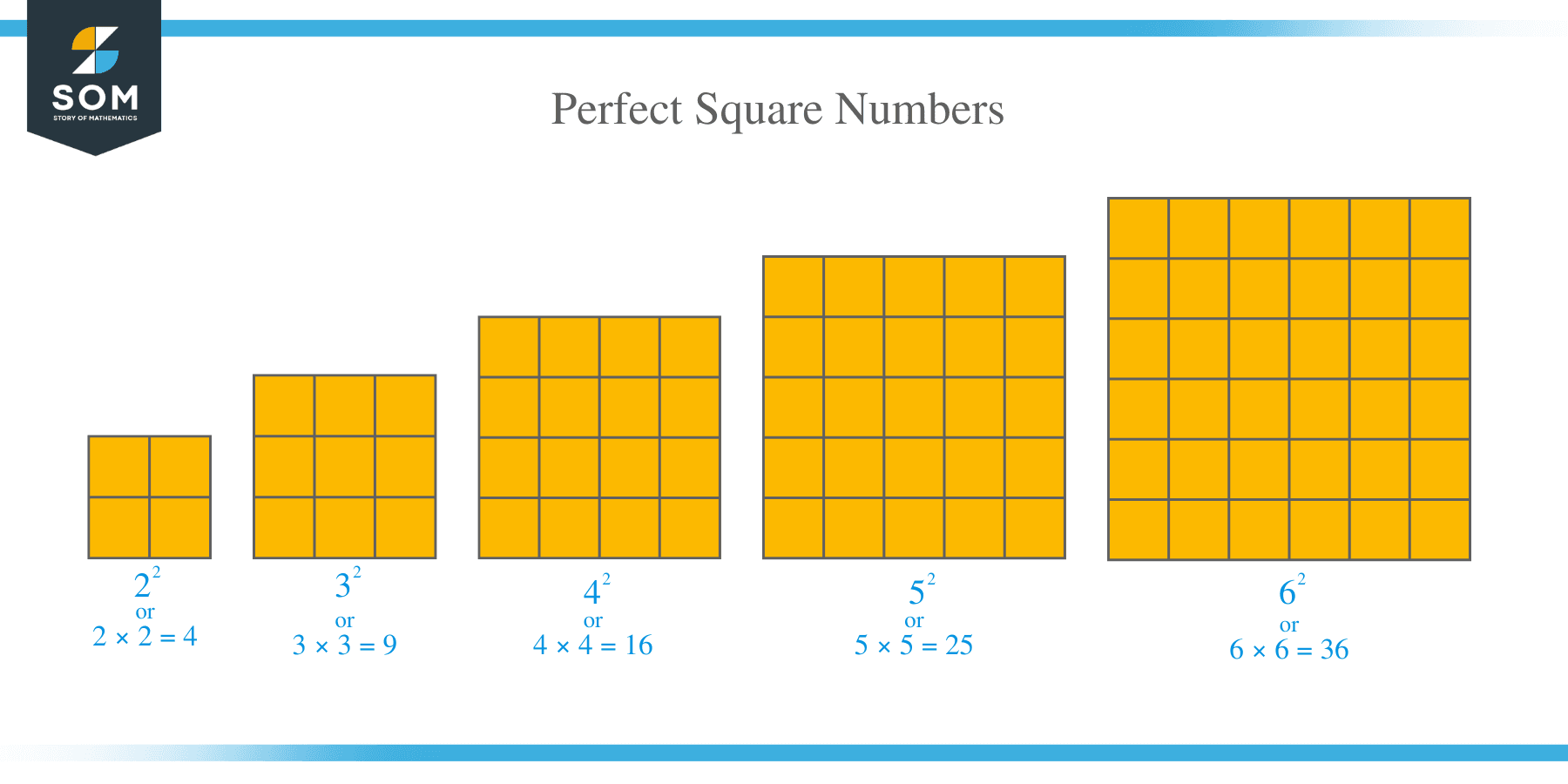

The first 25 perfect squares can be generated as shown in the table below:

Example 1

Integer	Perfect square
1 x 1	1
2 x 2	4
3 x 3	9
4 x 4	16
5 x 5	25
6 x 6	36
7 x 7	49
8 x 8	64
9 x 9	81
10 x 10	100
11 x 11	121
12 x 12	144
13 x 13	169
14 x 14	196
15 x 15	225
16 x 16	256
17 x 17	289
18 x 18	324
19 x 19	361
20 x 20	400
21 x 21	441
22 x 22	484
23 x 23	529
24 x 24	576
25 x 25	625

 

How can you tell if a number is a Perfect Square?

There are many ways of determining if a number is perfect. A given number can be checked whether it is a perfect square using repeated division by prime factors.

Example 2

For example, to check whether 441 is a perfect square:

• Start by factorizing a number.

441 = 3 × 3 × 7 × 7

• Both numbers exist twice. Make two sets.
  441 = 3 × 7 × 3 × 7
• Multiply them.

= 21 × 21

• It can be written as

= 21²

• Hence, 441 is a perfect square.

You can also check whether a given number is a perfect square by finding the number’s square root. If the square root of a number is a whole number, then the number is a perfect square

For instance, the square root of 16 is 4. The square root of a number like 24 is not a whole number. Therefore, 24 is not a perfect square.