
The aim of this question is to develop understanding by visualizing the flow of vector fields.
To draw a vector field, we use the following steps:
a) Convert the given function in the vector notation (vector components form).
b) Define some arbitrary points in the vector space.
c) Evaluate vector values at each of these points using the given function.
d) Evaluate the absolute starting point (the arbitrary points) and the absolute ending point (arbitrary point + vector values).
Draw all of the above vectors such that each vector starts from the above starting point and ends on the above-calculated ending point.
Expert Answer
The given equation is:
\[f(x,y) = \dfrac{yi+xj}{\sqrt{x^2+y^2}}\]
Rewriting in vector form:
\[f(x,y) = \bigg\langle\dfrac{y}{\sqrt{x^2+y^2}},\dfrac{x}{\sqrt{x^2+y^2}}\bigg\rangle\]
To draw the vector field we need to evaluate above vector function at some points. Lets choose following points:
\[(0,1),(0,-1),(1,0),(-1,0)\]
\[(0,2),(0,-2),(2,0),(-2,0)\]
\[(1,1),(1,-1),(-1,1),(-1,-1)\]
Now lets find these vectors one by one,
Evaluating at (0,1):
\[f(0,1) = \bigg\langle\dfrac{1}{\sqrt{(0)^2+(1)^2}},\dfrac{0}{\sqrt{(0)^2+(1)^2}}\bigg\rangle\]
\[f(0,1) = \bigg \langle\dfrac{1}{1},\dfrac{0}{1}\bigg\rangle\]
\[f(0,1) =\langle 1,0 \rangle \]
\[\text{Vector end point }\ =\ <0,1>\ +\ <1,0>\ =\ <1,1>\]
Evaluating at (0,-1):
\[f(0,-1) = \bigg\langle\dfrac{-1}{\sqrt{(0)^2+(-1)^2}},\dfrac{0}{\sqrt{(0)^2+(-1)^2}}\bigg\rangle\]
\[f(0,-1) = \bigg \langle\dfrac{-1}{1},\dfrac{0}{1}\bigg\rangle\]
\[f(0,-1) =\langle -1,0 \rangle\]
\[\text{Vector end point }\ =\ <0,-1>\ +\ <-1,0>\ =\ <-1,-1>\]
Evaluating at (1,0):
\[f(1,0) = \bigg\langle\dfrac{0}{\sqrt{(1)^2+(0)^2}},\dfrac{1}{\sqrt{(1)^2+(0)^2}}\bigg\rangle\]
\[f(1,0) = \bigg \langle\dfrac{0}{1},\dfrac{1}{1}\bigg\rangle\]
\[f(1,0) =\langle 0,1 \rangle\]
\[\text{Vector end point }\ =\ <1,0>\ +\ <0,1>\ =\ <1,1>\]
Evaluating at (-1,0):
\[f(-1,0) = \bigg\langle\dfrac{0}{\sqrt{(-1)^2+(0)^2}},\dfrac{-1}{\sqrt{(-1)^2+(0)^2}}\bigg\rangle\]
\[f(-1,0) = \bigg \langle\dfrac{0}{1},\dfrac{-1}{1}\bigg\rangle\]
\[f(-1,0) =\langle 0,-1 \rangle\]
\[\text{Vector end point }\ =\ <-1,0>\ +\ <0,-1>\ =\ <-1,-1>\]
Evaluating at (0,2):
\[f(0,2) = \bigg\langle\dfrac{2}{\sqrt{(0)^2+(2)^2}},\dfrac{0}{\sqrt{(0)^2+(2)^2}}\bigg\rangle\]
\[f(0,2) = \bigg \langle\dfrac{2}{2},\dfrac{0}{2}\bigg\rangle\]
\[f(0,2) =\langle 1,0 \rangle \]
\[\text{Vector end point }\ =\ <0,2>\ +\ <1,0>\ =\ <1,2>\]
Evaluating at (0,-2):
\[f(0,-2) = \bigg\langle\dfrac{-2}{\sqrt{(0)^2+(-2)^2}},\dfrac{0}{\sqrt{(0)^2+(-2)^2}}\bigg\rangle\]
\[f(0,-2) = \bigg \langle\dfrac{-2}{2},\dfrac{0}{2}\bigg\rangle\]
\[f(0,-2) =\langle -1,0 \rangle \]
\[\text{Vector end point }\ =\ <0,-2>\ +\ <-1,0>\ =\ <-1,-2>\]
Evaluating at (2,0):
\[f(2,0) = \bigg\langle\dfrac{0}{\sqrt{(0)^2+(2)^2}},\dfrac{2}{\sqrt{(0)^2+(2)^2}}\bigg\rangle\]
\[f(2,0) = \bigg \langle\dfrac{0}{2},\dfrac{2}{2}\bigg\rangle\]
\[f(2,0) =\langle 0,1 \rangle \]
\[\text{Vector end point }\ =\ <2,0>\ +\ <0,1>\ =\ <2,1>\]
Evaluating at (-2,0):
\[f(-2,0) = \bigg\langle\dfrac{0}{\sqrt{(0)^2+(-2)^2}},\dfrac{-2}{\sqrt{(0)^2+(-2)^2}}\bigg\rangle\]
\[f(-2,0) = \bigg \langle\dfrac{0}{2},\dfrac{-2}{2}\bigg\rangle\]
\[f(-2,0) =\langle 0,-1 \rangle \]
\[\text{Vector end point }\ =\ <-2,0>\ +\ <0,-1>\ =\ <-2,-1>\]
Evaluating at (1,1):
\[f(1,1) = \bigg\langle\dfrac{1}{\sqrt{(1)^2+(1)^2}},\dfrac{1}{\sqrt{(1)^2+(1)^2}}\bigg\rangle\]
\[f(1,1) = \bigg \langle\dfrac{1}{1.41},\dfrac{1}{1.41}\bigg\rangle\]
\[f(1,1) =\langle 0.707,0.707 \rangle \]
\[\text{Vector end point }\ =\ <1,1>\ +\ <0.707,0.707>\ =\ <1.707,1.707>\]
Evaluating at (1,-1):
\[f(1,-1) = \bigg\langle\dfrac{-1}{\sqrt{(1)^2+(-1)^2}},\dfrac{1}{\sqrt{(1)^2+(-1)^2}}\bigg\rangle\]
\[f(1,-1) = \bigg \langle\dfrac{-1}{1.41},\dfrac{1}{1.41}\bigg\rangle\]
\[f(1,-1) =\langle -0.707,0.707 \rangle \]
\[\text{Vector end point }\ =\ <1,-1>\ +\ <-0.707,0.707>\ =\ <0.293,-0.293>\]
Evaluating at (-1,1):
\[f(-1,1) = \bigg\langle\dfrac{1}{\sqrt{(-1)^2+(1)^2}},\dfrac{-1}{\sqrt{(-1)^2+(1)^2}}\bigg\rangle\]
\[f(-1,1) = \bigg \langle\dfrac{1}{1.41},\dfrac{-1}{1.41}\bigg\rangle\]
\[f(-1,1) =\langle 0.707,-0.707 \rangle \]
\[ \text{Vector end point }\ =\ <-1,1>\ +\ <0.707,-0.707>\ =\ <-0.293,0.293> \]
Evaluating at (-1,-1):
\[ f(-1,-1) = \bigg\langle\dfrac{1}{\sqrt{(-1)^2+(-1)^2}},\dfrac{-1}{\sqrt{(-1)^2+(-1)^2}}\bigg\rangle \]
\[ f(-1,-1) = \bigg \langle\dfrac{-1}{1.41},\dfrac{-1}{1.41}\bigg\rangle \]
\[ f(-1,-1) =\langle -0.707,-0.707 \rangle \]
\[ \text{Vector end point }\ =\ <-1,-1>\ +\ <-0.707,-0.707>\ =\ <-1.707,-1.707> \]
Numerical Result
Vector field of $f(x,y) = \dfrac{yi+xj}{\sqrt{x^2+y^2}}$ is shown below:
Diagram of the Vector Field:
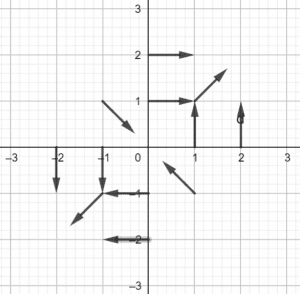
Figure 1
Example
To sketch the vector field of:
\[F(x,y) = -yi+xj\]
Evaluate following starting/ending pair points:
\[<1,0>|<1,1>\]
\[<0,1>|<-1,1>\]
\[<-1,0>|<-1,-1>\]
\[<0,-1>|<1,-1>\]
\[<3,0>|<3,3>\]
\[<0,3>|<-3,3>\]
\[<-3,0>|<-3,-3>\]
\[<0,-3>|<3,-3>\]
Plot the above points:
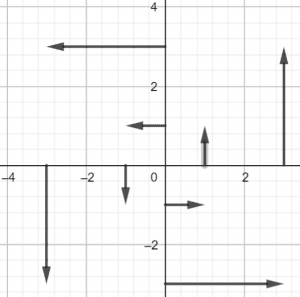
Figure 2: Vector field of $fF(x,y) = -yi+xj$
Images/ Mathematical drawings are created with Geogebra.
