Sine – Explanation & Examples

Have you ever realized you can determine sine function or any other trigonometric function by simply dividing one leg of a right triangle by another leg? That’s how simple, interesting — and beautiful — trigonometry is. We need to determine which sides of the right triangle are we dealing with from the perspective of the reference angle.

The sine function is defined by determining the ratio of the length of the side opposite a reference angle (acute angle) to the length of the hypotenuse of a right triangle.

After studying this lesson, we are expected to learn the concepts driven by these questions and be qualified to address accurate, specific, and consistent answers to these questions.

• What is a sine function?
• How can we determine the formula for sine function from a right-angled triangle?
• How can we solve actual problems using trigonometric functions?

The goal of this lesson is to clear up any confusion you might have about the concepts involving sine function.

What is sine?

In the context of a right triangle, the sine function is simply the ratio of the opposite side to the hypotenuse. For an angle $\alpha$, the sine function is simply denoted by $\sin \alpha$. In other words, sine is a trigonometric function of any given angle.

The following figure 3-1 represents a typical right triangle. The lengths of the three legs (sides) of the right triangle are named $a$, $b$, and $c$. The angles opposite the legs of lengths $a$, $b$, and $c$ are named $\alpha$, $\beta$, and $\gamma$. The tiny square with the angle $\gamma$ shows that it is a right angle.

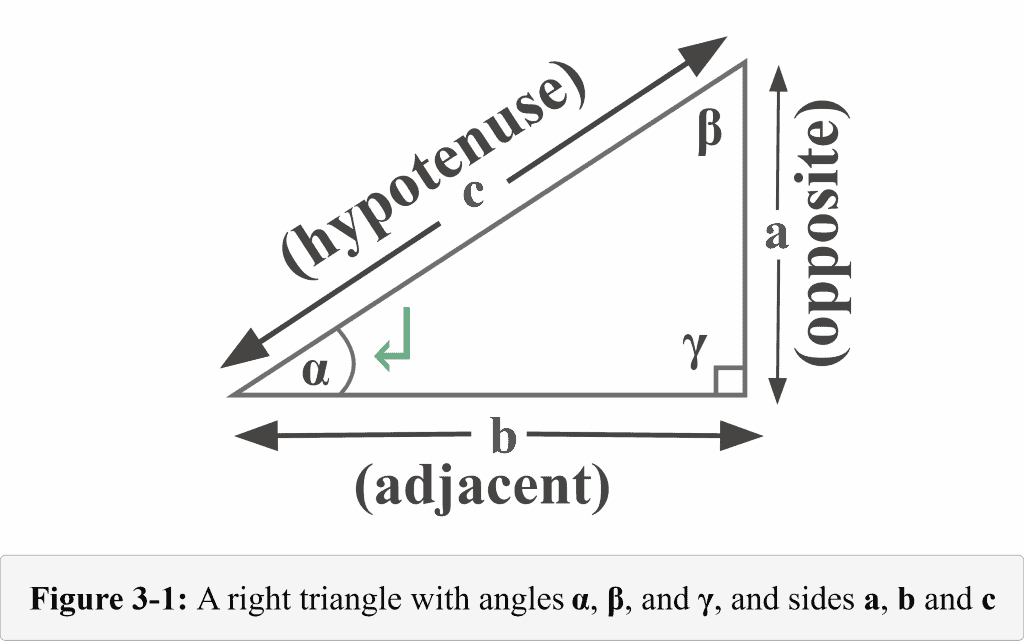
Use the diagram in Figure 3-1 to determine the sine function from the perspective of the angle $\alpha$.

Looking at Figure 3-1, we can determine the sine function from the right-angled triangle if we divide the length of the side opposite the reference angle $\alpha$ (acute angle) by the length of the hypotenuse.

The following figure 3-2 represents a sine function.

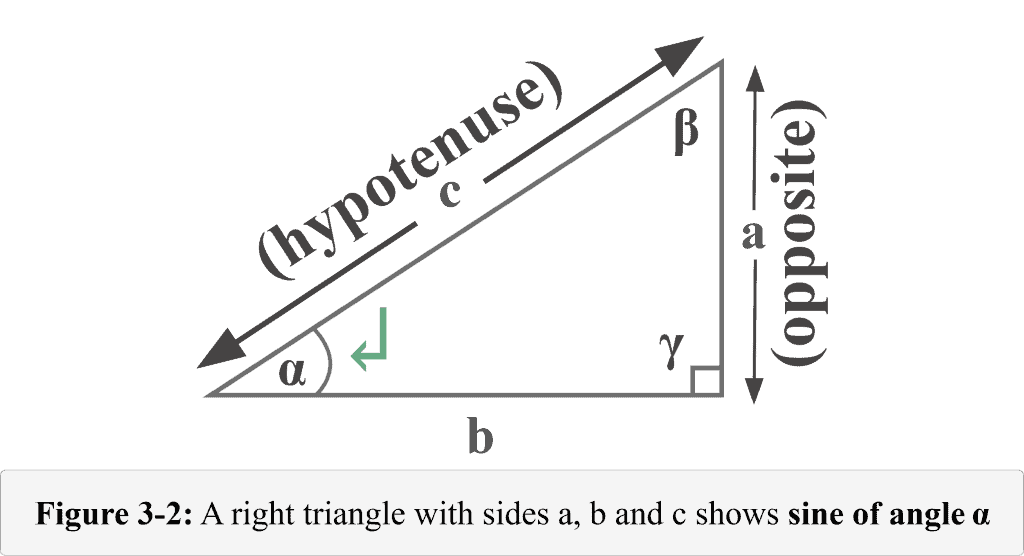
Looking at Figure 3-2, we can identify that the side of length $a$ is the opposite side that lies exactly opposite the reference angle $\alpha$, and the side of length $c$ is the hypotenuse. Thus,

Opposite = $a$

Hypotenuse = $c$

Therefore, the sine of an angle $\alpha$ is

${\displaystyle \sin \alpha =\frac{a}{c}}$

Therefore, we conclude that the sine function is the ratio of the opposite side to the hypotenuse.

Sine function from the perspective of the angle $\beta$

We should be cautious when we apply the terms opposite and adjacent because the meaning of these terms is dependent on the reference angle we are using.

The following figure 3-3 represents a typical right triangle from the perspective of the angle $\beta$.

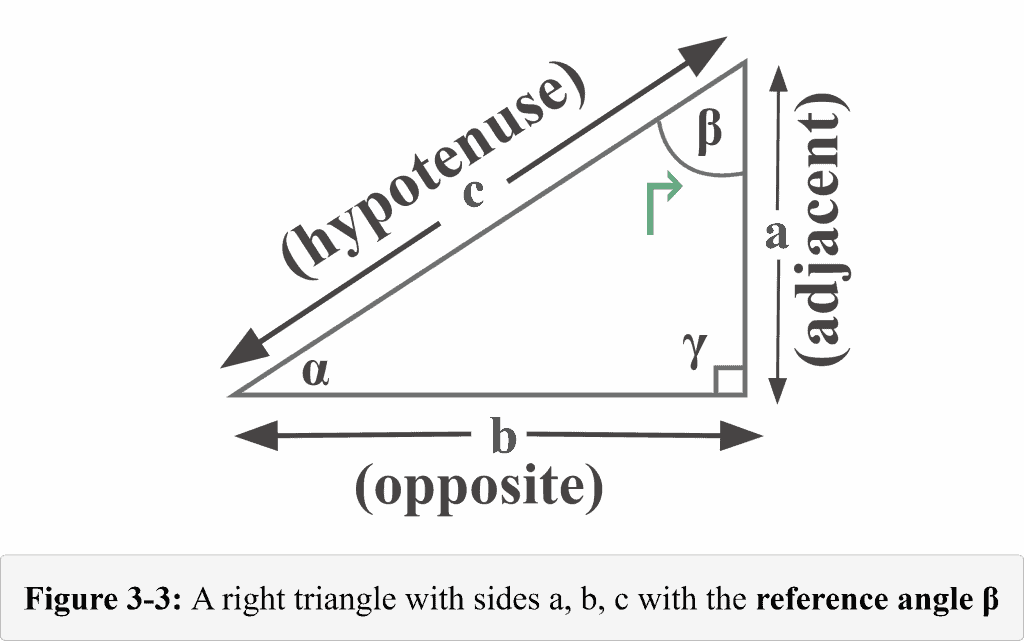
You can observe that now the roles of the sides have been shifted.

Looking at Figure 3-3, it is clear now the length of the side $a$ is right next to the reference angle $\beta$, and the length of the side $b$  lies exactly opposite the reference angle $\beta$. Thus, in relation to the angle measuring $\beta$, now we have

Adjacent = $a$

Opposite = $b$

While the hypotenuse $c$ remains the same. This is why the hypotenuse is very special in a right-angled triangle.

The following figure 3-4 represents a sine function from the perspective of the angle $\beta$.

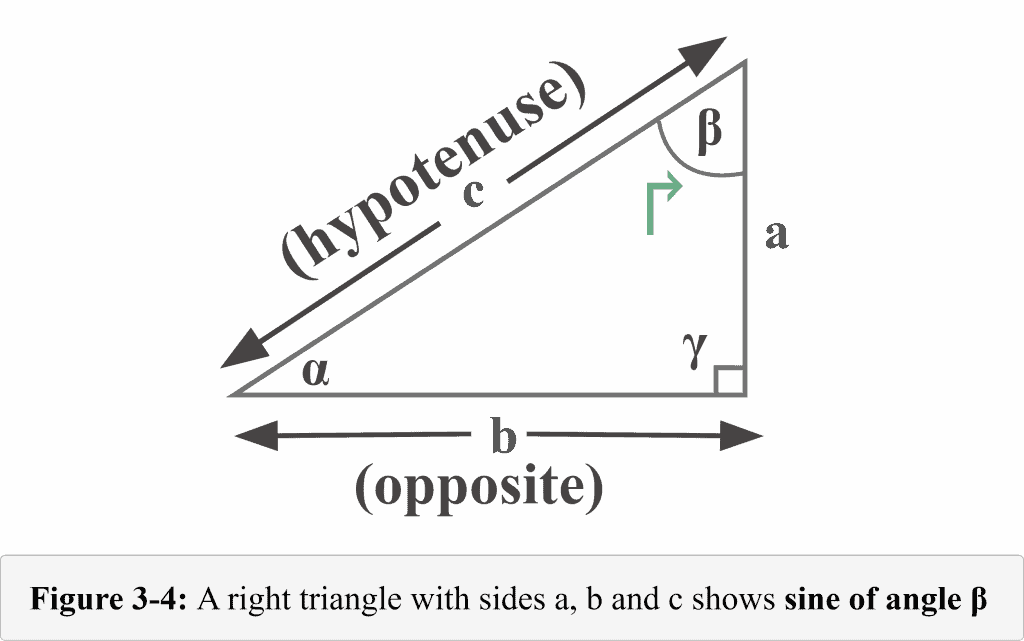
Looking at Figure 3-4, we can identify that the side of length $b$ is the opposite side that lies exactly opposite the reference angle $\beta$, and the side of length $c$ is the hypotenuse. Thus,

Opposite = $b$

Hypotenuse = $c$

We know that the sine function is the ratio of the opposite side to the hypotenuse.

Therefore, the sine of an angle $\beta$ is

${\displaystyle \sin \beta =\frac{b}{c}}$

What is the formula for sine?

The following figure 3-5 illustrates a clear comparison of how we determined the ratios of sine function from the perspective of both the angles$\alpha$ and $\beta$.

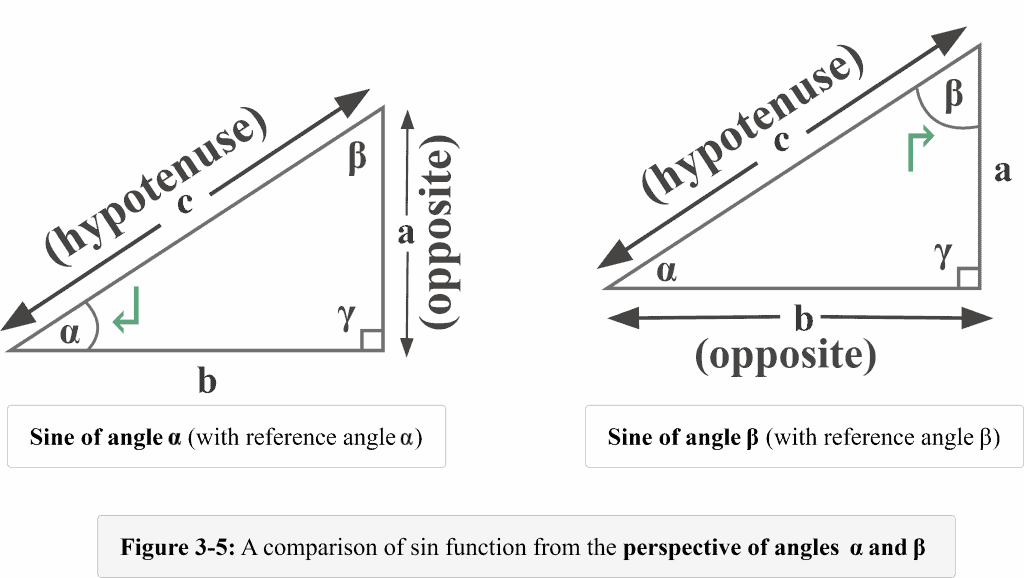
The comparison clearly indicates that the sine function is the ratio obtained when we divide the length of the side opposite the mentioned reference angle by the length of the hypotenuse.

Here:

${\displaystyle \sin \alpha =\frac{a}{c}}$

Thus,

Similarly,

${\displaystyle \sin \beta =\frac{b}{c}}$

Thus,

Therefore, we conclude that the sine function is the ratio of the opposite side to the hypotenuse.

How to remember the formula of the sine function?

We created the SOH – CAH – TOA table in previous lessons to remember the formulae of the trigonometric functions. You must memorize the first portion — SOH — of the code-word SOH – CAH – TOA to remember the formula of the sine function.

Here is the table:

               ↑

YOU ARE HERE!

Example $1$

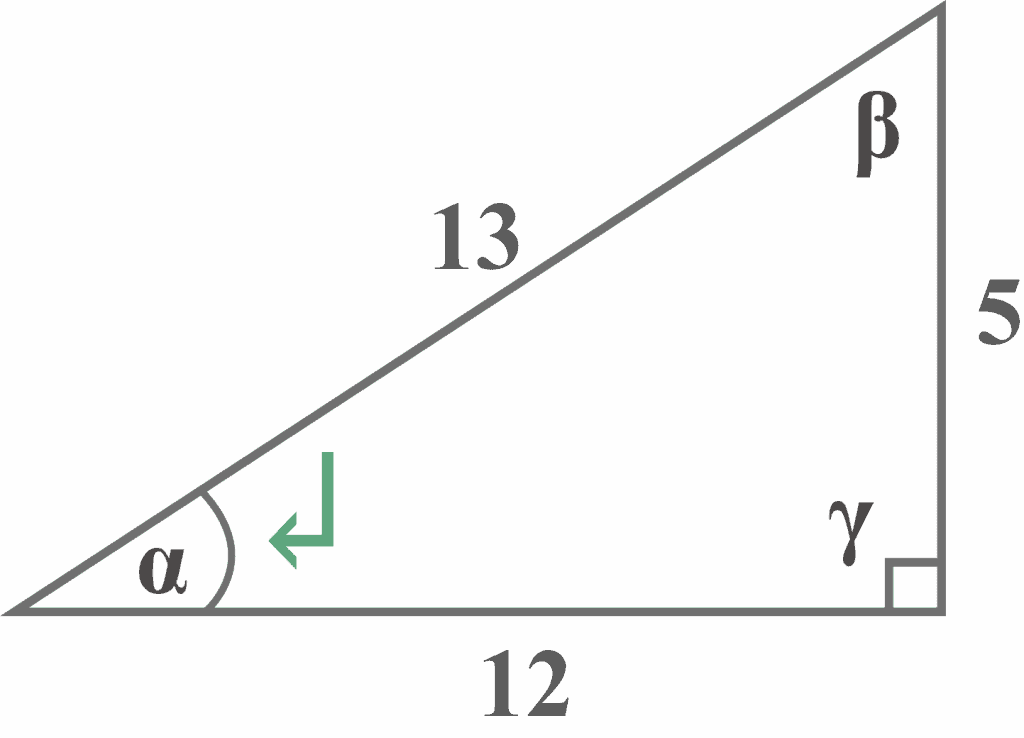
Given a right-angled triangle with the reference angle $\alpha$. What is the sine of angle $\alpha$?

Solution:

Looking at the diagram, it is clear that the side of length $5$ is the opposite side that lies exactly opposite the reference angle $\alpha$, and the side of length $13$ is the hypotenuse. Thus,

Opposite = $5$

Hypotenuse = $13$

We know that sine function is the ratio of the opposite side to the hypotenuse.

${\displaystyle \sin \alpha =\frac{\mathrm{opposite}}{\mathrm{hypotenuse}}}$

Therefore, the sine of angle $\alpha$ is:

Example 2

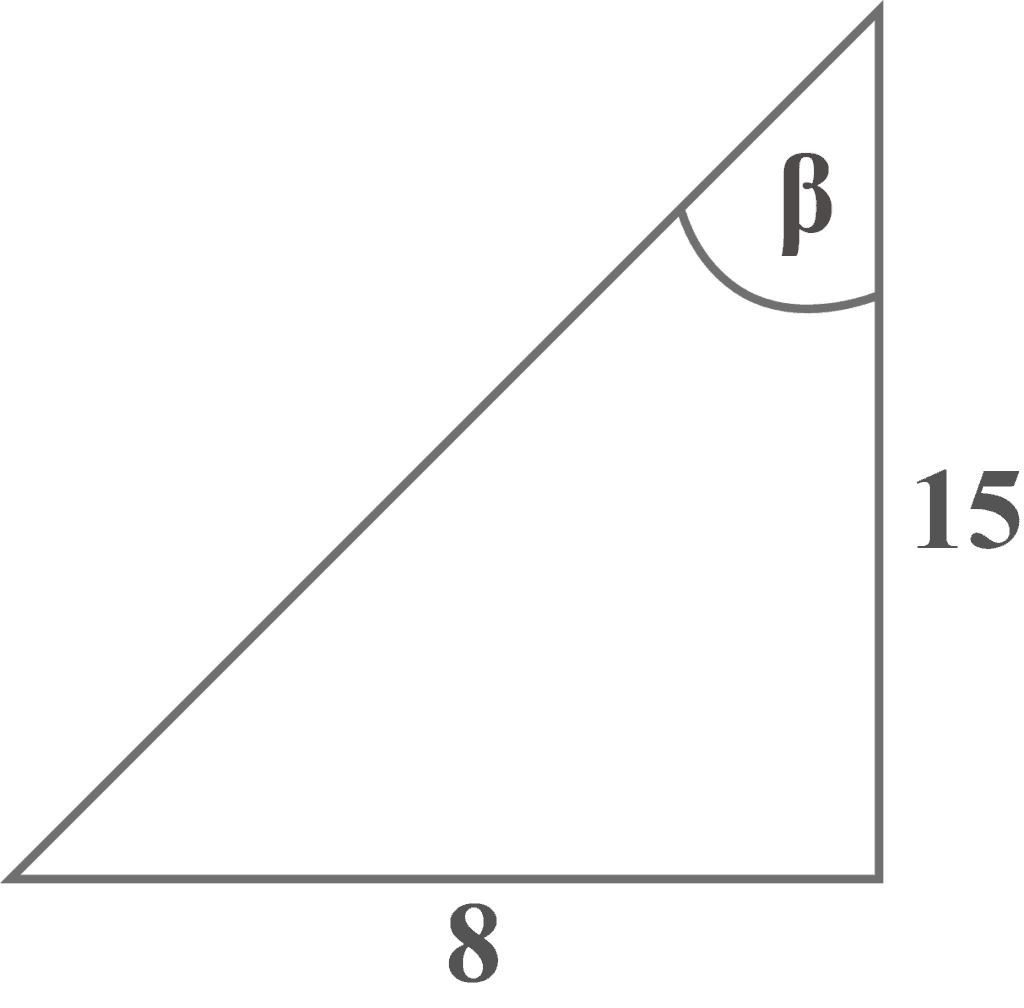
Given a right-angled triangle with the reference angle $\beta$. What is the sine of angle $\beta$?

Solution:

Looking at the diagram, it is clear that the side of length $8$ is the opposite side that lies exactly opposite the reference angle $\beta$. Also, the length of side $15$ is right next to the reference angle $\beta$.

We have to determine the sine of angle $\beta$. All right, here comes the tricky part.

We know that the sine function is the ratio of the opposite side to the hypotenuse, but the length of the hypotenuse is missing. What should we do?

Step 1: Determine the unknown but relevant side — the hypotenuse.

To determine the hypotenuse, we need to use the Pythagoras theorem,

$c^2=a^2+b^2$

looking at the diagram, we have:

Opposite $b=8$

Adjacent $a=15$

Hypotenuse $c=$?

Substitute $a=15$ and $b=8$ in the formula

$c^2={15}^2+8^2$

$c^2=225+64$

$c^2=289$

$c=17$ units

Thus, the length of the hypotenuse is $17$ units.

Step 2: Determine the sine of angle β.

Now, we have:

Opposite $=8$

Hypotenuse $=17$

Using the formula of the sine function

${\displaystyle \sin \beta =\frac{\mathrm{opposite}}{\mathrm{hypotenuse}}}$

Therefore, the sine of angle β is:

Example 3

Given a right-angled triangle with the reference angle $\alpha$. Which option represents the trigonometric ratio of $\frac{7}{25}$?

       a) $\sin \alpha$

       b) $\cos \alpha$

       c) $\tan \alpha$

       d) $\cot \alpha$

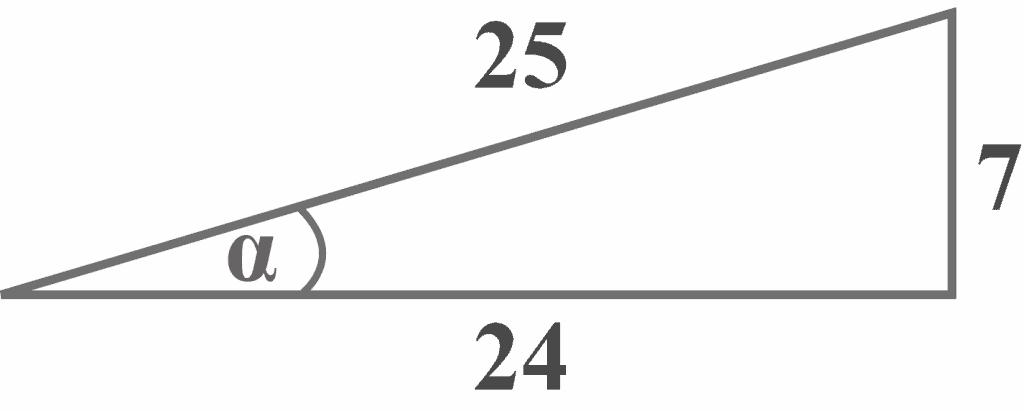
Looking at the diagram, it is clear that the side of length $7$ is the opposite side that lies exactly opposite the reference angle $\alpha$, and the side of length $25$ is the hypotenuse.

Thus,

Opposite = $7$

Hypotenuse = $25$

We know that formula of the sine function is

${\displaystyle \sin \alpha =\frac{\mathrm{opposite}}{\mathrm{hypotenuse}}}$

Thus,

Therefore, option a) is the true choice.

Example 4

Victoria leans her stair against the wall to reach the top of the building. The stair length is $18$ feet long, and the angle formed is ${60}^{\circ }$. What should be the base length of the stair? A Figure is illustrated below to give you a hint.

Solution:

We know that the sum of angles in a triangle is ${180}^{\circ }$.

As the given triangle is right-angled, and one of the angles is ${60}^{\circ }$. We need to determine the unknown angle. Let the unknown angle be θ.

${60}^{\circ }+{90}^{\circ }+\theta ={180}^{\circ }$

${150}^{\circ }+\theta ={180}^{\circ }$

$\theta ={30}^{\circ }$

Check the diagram below.

Looking at the diagram, the base of the stair is the opposite side that lies exactly opposite the angle $\theta ={30}^{\circ }$.

Therefore, to determine the base length, we need to find the opposite side’s length that lies exactly opposite the angle $\theta ={30}^{\circ }$.

Let $x$ be the required base length.

Now, we have:

• Hypotenuse = $18$ feet
• $\theta ={30}^{\circ }$
• Base of the stair = Opposite = $x$

As the relevant sides involve hypotenuse and opposite, so we use the formula of the sine function

${\displaystyle \sin \theta =\frac{\mathrm{opposite}}{\mathrm{hypotenuse}}}$

substitute $\theta ={30}^{\circ }$, opposite = $x$, and hypotenuse = $18$ in the formula

${\displaystyle \sin {30}^{\circ }=\frac{x}{18}}$

As

$\sin {30}^{\circ }=0.5$ (check using a calculator)

Thus,

$0.5=\frac{x}{18}$

$x=(0.5)(18)$

$x=9$ feet

Therefore, the base of the stair is $x=9$ feet.