Simplifying Radicals – Techniques & Examples

The word radical in Latin and Greek means “root” and “branch,” respectively. The idea of radicals can be attributed to exponentiation or raising a number to a given power.

The concept of radical is mathematically represented as x ⁿ. This expression tells us that a number x is multiplied by itself n number of times. For instance,

3 ² = 3 × 3 = 9, and 2 ⁴ = 2 × 2 × 2 × 2 = 16.

How to Simplify Radicals?

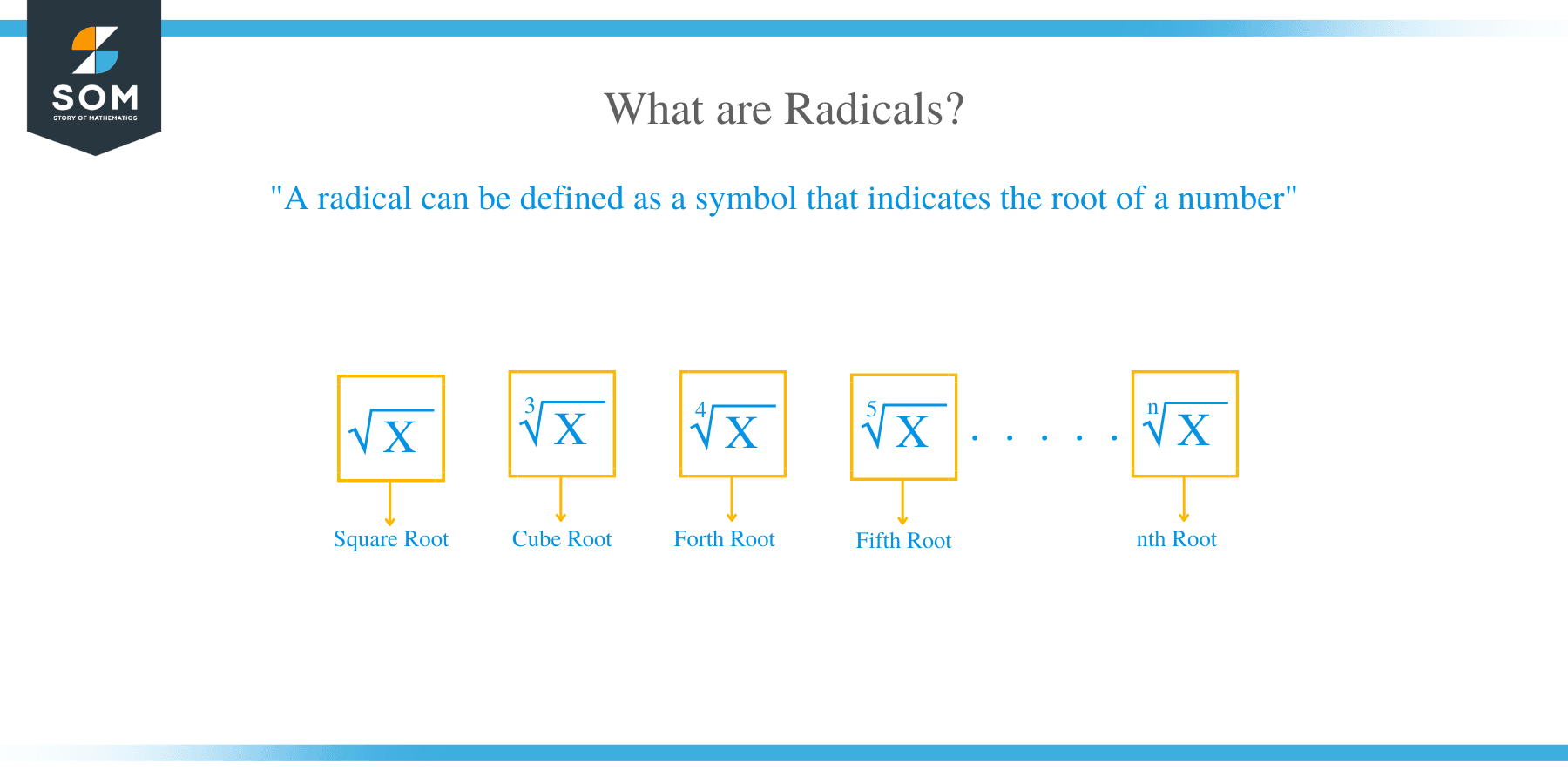
The following are the steps required for simplifying radicals:

• Start by finding the prime factors of the number under the radical. Divide the number by prime factors such as 2, 3, 5 until only the left numbers are prime.
• Determine the index of the radical. The index of the radical tells the number of times you need to remove the number from inside to outside radical.
• Move only variables that make groups of 2 or 3 from inside to outside radicals.
• Simplify the expressions both inside and outside the radical by multiplying.
• Simplify by multiplication of all variables both inside and outside the radical.

Example 1

Simplify: √252

Solution

• Find the prime factors of the number inside the radical.

252 = 2 x 2 x 3 x 3 x 7

• Find the radical index, and for this case, our index is two because it is a square root. Therefore, we need two of a kind.

√ (2 x 2 x 3 x 3 x 7)

• Now pull each group of variables from inside to outside the radical. In this case, the pairs of 2 and 3 are moved outside.

2 x 3 √7

• By multiplication, simplify both the expression inside and outside the radical to get the final answer as:

6 √7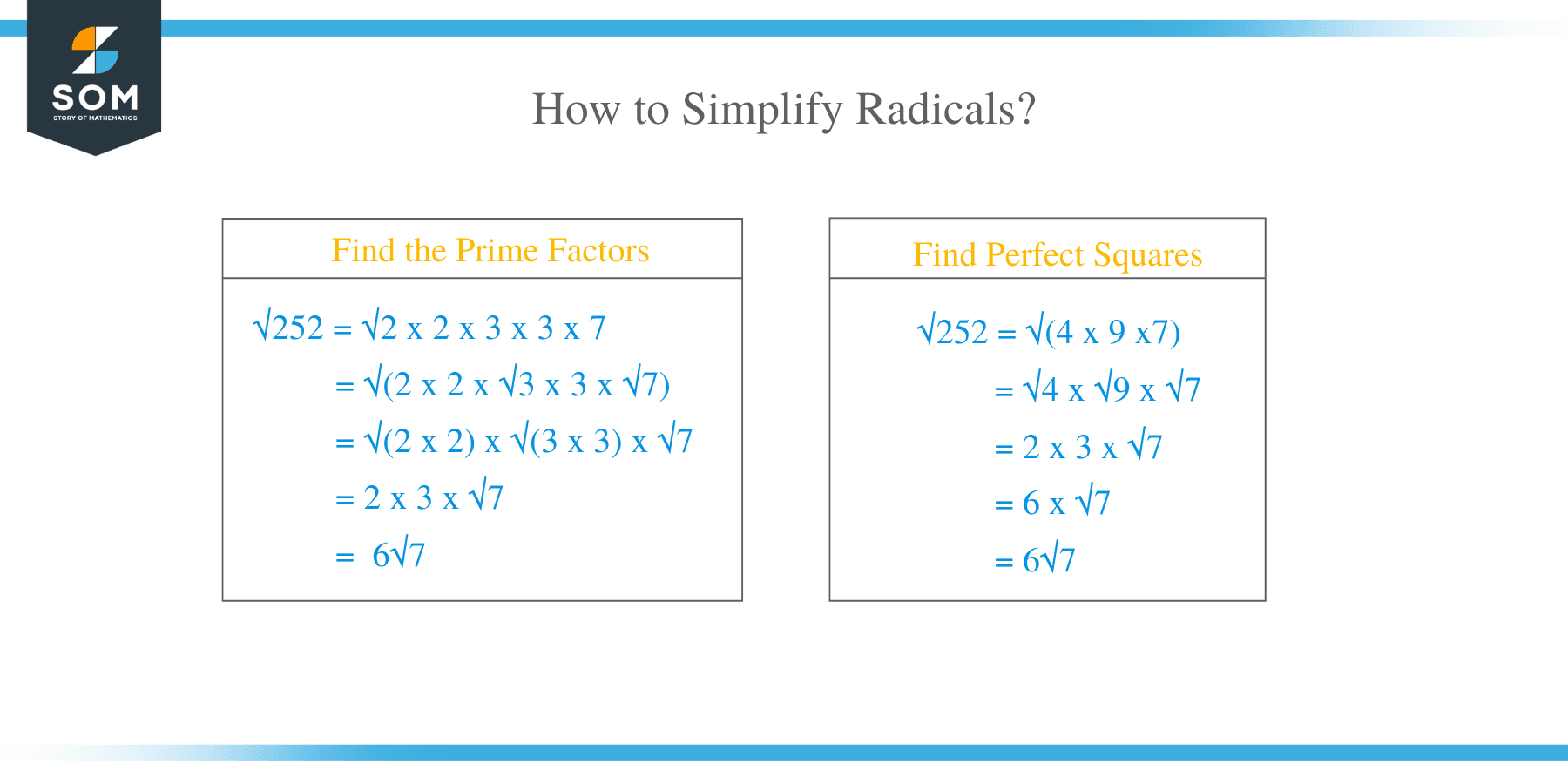

Example 2

Simplify:

³√(-432x ⁷ y ⁵)

Solution

• To solve such a problem, first, determine the prime factors of the number inside the radical.

432 = 2 x 2 x 2 x2 x 3 x 3 x 3

• Because, it is cube root, then our index is 3.

–³√(2 x 2 x 2 x2 x 3 x 3 x 3 x x ⁷ x y ⁵)

• Extract each group of variables from inside the radical, and these are 2, 3, x, and y.

-2 x 3 x y ³ x x√(2xy ²)

• Multiply the variables both outside and inside the radical.

-6xy ³√(2xy ²)

Example 3

Solve the following radical problem.

Find the value of a number n if the square root of the sum of the number with 12 is 5.

Solution

• Write an expression of this problem, square root of the sum of n and 12 is 5
  √(n + 12) = square root of the sum.

√(n + 12)=5

• Our equation which should be solved now, is:

√(n + 12) = 5

• On each side the equation is squared:

[√(n + 12)]² = 5²
[√(n + 12)] x [√(n + 12)] = 25
√[(n + 12) x √(n + 12)] = 25
√(n + 12)² = 25
n + 12 = 25

• Subtract 12 from both sides of the expression

n + 12 – 12 = 25 – 12
n + 0 = 25 – 12
n = 13