Quadrilaterals in a Circle – Explanation & Examples

We have studied that a quadrilateral is a 4 – sided polygon with 4 angles and 4 vertices. For more details, you can consult the article “Quadrilaterals” in the “Polygon” section.

In geometry exams, examiners make the questions complex by inscribing a figure inside another figure and ask you to find the missing angle, length, or area. One example from the previous article shows how an inscribed triangle inside a circle makes two chords and follows certain theorems.

This article will discuss what a quadrilateral inscribed in a circle is and the inscribed quadrilateral theorem.

What is a Quadrilateral Inscribed in a Circle?

In geometry, a quadrilateral inscribed in a circle, also known as a cyclic quadrilateral or chordal quadrilateral, is a quadrilateral with four vertices on the circumference of a circle. In a quadrilateral inscribed circle, the four sides of the quadrilateral are the chords of the circle.

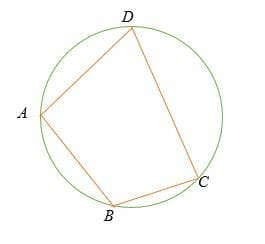
In the above illustration, the four vertices of the quadrilateral ABCD lie on the circle’s circumference. In this case, the diagram above is called a quadrilateral inscribed in a circle.

Inscribed Quadrilateral Theorem

There are two theorems about a cyclic quadrilateral. Let’s take a look.

Theorem 1

The first theorem about a cyclic quadrilateral state that:

The opposite angles in a cyclic quadrilateral are supplementary. i.e., the sum of the opposite angles is equal to 180˚.

Consider the diagram below.

If a, b, c, and d are the inscribed quadrilateral’s internal angles, then

a + b = 180˚ and c + d = 180˚.

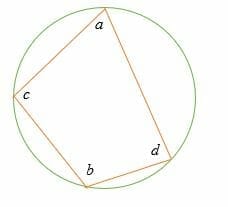
Let’s prove that;

• a + b = 180˚.

Join the vertices of the quadrilateral to the center of the circle.

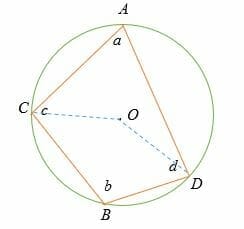
Recall the inscribed angle theorem (the central angle = 2 x inscribed angle).

∠COD = 2∠CBD

∠COD = 2b

Similarly, by intercepted arc theorem,

∠COD = 2 ∠CAD

∠COD = 2a

∠COD + reflex ∠COD = 360^o

2a + 2b = 360^o

2(a + b) =360^o

By dividing both sides by 2, we get

a + b = 180^o.

Hence proved!

Theorem 2

The second theorem about cyclic quadrilaterals states that:

The product of the diagonals of a quadrilateral inscribed in a circle is equal to the sum of the product of its two pairs of opposite sides.

Consider the following diagram, where a, b, c, and d are the sides of the cyclic quadrilateral and D₁ and D₂ are the quadrilateral diagonals.

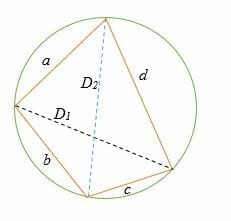
In the above illustration,

(a * c) + (b * d) = (D₁ * D₂)

Properties of a quadrilateral inscribed in a circle

There exist several interesting properties about a cyclic quadrilateral.

• All the four vertices of a quadrilateral inscribed in a circle lie on the circumference of the circle.
• The sum of two opposite angles in a cyclic quadrilateral is equal to 180 degrees (supplementary angles)
• The measure of an exterior angle is equal to the measure of the opposite interior angle.
• The product of the diagonals of a quadrilateral inscribed in a circle is equal to the sum of the product of its two pairs of opposite sides.
• The perpendicular bisectors of the four sides of the inscribed quadrilateral intersect at the center O.
• The area of a quadrilateral inscribed in a circle is given by Bret Schneider’s formula as:

Area = √[s(s-a) (s-b) (s – c) (s – c)]

where a, b, c, and d are the side lengths of the quadrilateral.

s = Semi perimeter of the quadrilateral = 0.5(a + b + c + d)

Let’s get an insight into the theorem by solving a few example problems.

Example 1

Find the measure of the missing angles x and y in the diagram below.

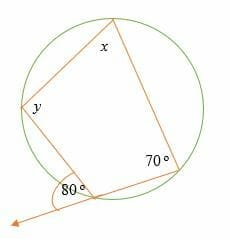
Solution

x = 80 ^o (the exterior angle = the opposite interior angle).

y + 70 ^o = 180 ^o (opposite angles are supplementary).

Subtract 70 ^o on both sides.

y = 110^o

Therefore, the measure of angles x and y are 80^o and 110^o, respectively.

Example 2

Find the measure of angle ∠QPS in the cyclic quadrilateral shown below.

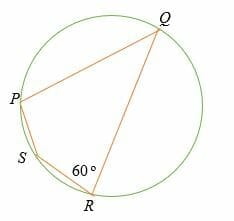
Solution

∠QPS is the opposite angle of ∠SRQ.

According to the inscribed quadrilateral theorem,

∠QPS + ∠SRQ = 180^o (Supplementary angles)

∠QPS + 60^o = 180^o

Subtract 60^o on both sides.

∠QPS = 120 ^o

So, the measure of angle ∠QPS is 120^o.

Example 3

Find the measure of all the angles of the following cyclic quadrilateral.

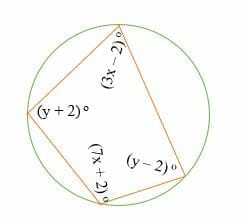
Solution

Sum of opposite angles = 180 ^o

(y + 2) ^o + (y – 2) ^o = 180 ^o

Simplify.

y + 2 + y – 2 =180 ^o

2y = 180 ^o

Divide by 2 on both sides to get,

y = 90 ^o

On substitution,

(y + 2) ^o ⇒ 92 ^o

(y – 2) ^o ⇒ 88 ^o

Similarly,

(3x – 2) ^o = (7x + 2) ^o

3x – 2 + 7x + 2 = 180 ^o

10x =180 ^o

Divide by 10 on both sides,

x = 18 ^o

Substitute.

(3x – 2) ^o ⇒ 52 ^o

(7x + 2) ^o ⇒ 128^o