The Pythagorean identities are derived from the Pythagorean theorem. We use these identities to simplify processes involving trigonometric expressions, equations and identities.
In this article, we’ll break down the proof of these three Pythagorean identities, show key applications of these identities, and provide ample examples to help you master this topic.
What Are the Pythagorean Identities?
The Pythagorean identities are the three most-used trigonometric identities that have been derived from the Pythagorean theorem, hence its name. Here are the three Pythagorean identities that we’ll learn and apply throughout our discussion.
\begin{aligned}\color{DarkOrange}\textbf{Pythagorean}\,\,\color{DarkOrange}\textbf{Iden}&\color{DarkOrange}\textbf{tities}\\\\\sin^2\theta + \cos^2 \theta = &1\\\tan^2 \theta +1= \sec^2 &\theta\\1+ \cot^2 \theta = \csc^2 &\theta\end{aligned}
The first Pythagorean identity is the most fundamental since it will be easier for us to derive the two remaining Pythagorean identities with this. From the first equation, the Pythagorean states that the sum of squares of $\sin \theta$ and $\cos \theta$ will always be equal to $1$.
\begin{aligned}\sin^2 45^{\circ} + \cos^2 45^{\circ} &= 1\\\sin^2 \left(\dfrac{2\pi}{3}\right) + \cos^2 \left(\dfrac{2\pi}{3}\right)&= 1\end{aligned}
Why don’t we evaluate the left-hand side of the equations to confirm that the Pythagorean identity $\sin^2 \theta + \cos^2\theta =1$ remain true for these two equations?
| \begin{aligned}\boldsymbol{\sin^2 45^{\circ} + \cos^2 45^{\circ}} &= \boldsymbol{1}\end{aligned} | \begin{aligned}\boldsymbol{\sin^2 \dfrac{2\pi}{3}+ \cos^2 \dfrac{2\pi}{3}}&= \boldsymbol{1}\end{aligned} |
| \begin{aligned}\sin^2 45^{\circ} + \cos^245^{\circ} &=1\\\left(\dfrac{1}{\sqrt{2}}\right)^2+ \left(\dfrac{1}{\sqrt{2}}\right)^2&= 1\\\dfrac{1}{2}+ \dfrac{1}{2}&=1\\1&=1 \checkmark\end{aligned} | \begin{aligned}\sin^2 \left(\dfrac{2\pi}{3}\right) + \cos^2\left(\dfrac{2\pi}{3}\right)&=1\\\left(\dfrac{\sqrt{3}}{2}\right)^2+ \left(-\dfrac{1}{2}\right)^2&= 1\\\dfrac{3}{4}+ \dfrac{1}{4}&=1\\1&=1 \checkmark\end{aligned} |
In fact, regardless of the value of $\theta$, the Pythagorean identity will remain true for all angle measures. This is what makes these identities helpful – we can simplify complex trigonometric expressions and use them to rewrite and prove identities.
For us to appreciate the Pythagorean identities, it’s important that we understand their origin and derivation first.
Pythagorean Identity Definition and Proof
Given an angle, $\theta$, the Pythagorean identities allow us to show the relationship between the squares of the trigonometric ratios. Let’s place our focus on the first Pythagorean identity.
\begin{aligned}\sin^2 \theta + \cos^2 \theta &= 1\end{aligned}
It’s most crucial to remember this Pythagorean identity – that’s because once we know this by heart, the two remaining Pythagorean identities will be easy to remember and derive.
For now, let’s understand that we can apply the Pythagorean Theorem to derive the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$.
Suppose that we have a unit circle. Observe the relationship between the sides of the right triangle formed inside the first quadrant of the unit circle as shown below.
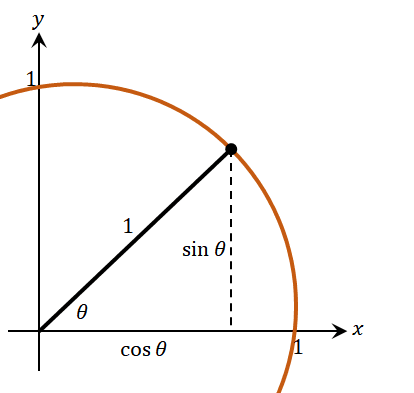
We know that the point lying on the unit circle has a coordinate of $(\sin \theta, \cos \theta)$. This means that the side adjacent to $\theta$ is equal to $\cos \theta$ and the side opposite $\theta$ is $\sin \theta$. Apply the Pythagorean theorem to relate the sides of the right triangle formed.
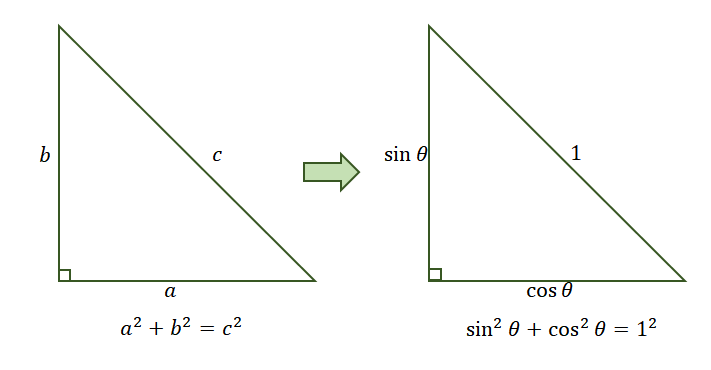
This means that the side adjacent to $\theta$ is equal to $\cos \theta$ and the side opposite $\theta$ is $\sin \theta$. Apply the Pythagorean theorem to relate the sides of the right triangle formed. This proves our first Pythagorean identity, $\sin^2\theta + \cos^2 \theta = 1$.
To prove that $\sec^2 \theta- \tan^2 \theta = 1$ is true, divide both sides of the equation by $\cos^2 \theta$. Apply the basic trigonometric identities $\sec \theta =\dfrac{1}{\cos\theta}$ and $\tan \theta =\dfrac{\sin \theta}{\cos \theta}$.
\begin{aligned}\sin^2\theta+\cos^2\theta &=1\\\dfrac{\sin^2\theta}{\color{DarkOrange}\cos^2\theta}+\dfrac{\cos^2\theta}{\color{DarkOrange}\cos^2\theta}&=\dfrac{1}{\color{DarkOrange}\cos^2\theta}\\\left(\dfrac{\sin\theta}{\cos\theta}\right)^2+1&=\left(\dfrac{1}{\cos\theta}\right)^2\\\color{DarkOrange}\boldsymbol{\tan^2 \theta + 1} &\color{DarkOrange}\boldsymbol{=\sec^2\theta}\end{aligned}
Derive the third Pythagorean identity by applying a similar process. This time, divide both sides of $\sin^2\theta + \cos^2\theta =1$ by $\sin^2\theta$. Use the trigonometric identities $\csc \theta =\dfrac{1}{\sin\theta}$ and $\cot \theta =\dfrac{\cos \theta}{\sin \theta}$ to simplify the identity.
\begin{aligned}\sin^2\theta + \cos^2 \theta &=1\\\dfrac{\sin^2\theta}{\color{DarkOrange}\sin^2\theta} +\dfrac{\cos^2\theta}{\color{DarkOrange}\sin^2\theta} &=\dfrac{1}{\color{DarkOrange}\sin^2\theta}\\1+ \left(\dfrac{\cos\theta}{\sin\theta}\right)^2&= \left(\dfrac{1}{\sin\theta}\right)^2\\\color{DarkOrange}\boldsymbol{1 + \cot^2 \theta} &\color{DarkOrange}\boldsymbol{=\csc^2\theta}\end{aligned}
Now that we’ve shown you how the identities were derived, it’s time for us to learn how to apply them in solving problems and proving other trigonometric identities.
How To Use the Pythagorean Identity?
The Pythagorean identity can be used to solve equations, evaluate expressions, and prove identities by rewriting trigonometric expressions using the three identities. This is how to use the Pythagorean identities.
\begin{aligned}\sin^2\theta + \cos^2 \theta = &1\\\tan^2 \theta +1= \sec^2 &\theta\\1+ \cot^2 \theta = \csc^2 &\theta\end{aligned}
Evaluating Expressions Using Pythagorean Identities
When using the Pythagorean identity to evaluate expressions, we can:
- Identify which of the three identities will be the most helpful.
- Use the given values into the chosen Pythagorean identity, then solve for the unknown value.
Suppose that $\sin \theta = \dfrac{12}{13}$ and $\theta$ is located at the first quadrant, we can find the exact value of $\cos \theta$ by using the Pythagorean identity. Since we’re working with sine and cosine, let’s use the first Pythagorean identity.
\begin{aligned}\sin^2\theta + \cos^2\theta = 1\end{aligned}
Substitute $\sin \theta = \dfrac{12}{13}$ into the Pythagorean identity. Simplify the equation to find the exact value of $\cos \theta$.
\begin{aligned}\sin^2\theta+ \cos^2 \theta &= 1\\\left({\color{DarkOrange}\dfrac{12}{13}}\right)^2 +\cos^2 \theta &= 1\\\dfrac{144}{169}+\cos^2 \theta &= 1\\\cos^2\theta&= \dfrac{25}{169}\\\cos \theta &= \pm \dfrac{5}{13}\end{aligned}
The angle, $\theta$, lies on the first quadrant, so $\cos \theta$ is positive. Hence, $\cos \theta = \dfrac{5}{13}$.
Apply a similar process when asked to find the exact values of other trigonometric expressions. For now, let’s take a look at how we can use the Pythagorean identities when solving trigonometric equations.
Solving Equations Using Pythagorean Identities
When given a trigonometric equation, see whether we can rewrite any of the terms using the Pythagorean identities. These terms are normally those that contain the terms from the three Pythagorean identities.
- When either $\sin \theta$ and $\cos \theta$ are part of the equation and at least one of them is squared
- Similarly, when $\sec \theta$ and $\tan \theta$ are present as well as $\csc \theta$ and $\cot \theta$
- To simplify the equation, rewrite one of the trigonometric expression in terms of the other
Let’s say that we want to solve for $\theta$ in the equation $1 – \sec^2\theta -\tan \theta = 0$. We can see that the equation contains $\sec^2 \theta$ and $\tan \theta$, so rewrite $\sec^2 \theta$ using the Pythagorean identity $\tan^2 \theta +1 = \sec^2 \theta$.
\begin{aligned}1 – \sec^2\theta &= \tan \theta\\1 – {\color{DarkOrange}(\tan^2 \theta +1 )} &= \tan \theta\\1 -\tan^2\theta -1&= \tan\theta\\\tan^2\theta +\tan\theta&=0\end{aligned}
We now have a quadratic equation with only $\tan \theta$ and $\tan^2{\theta}$ to worry about. Apply appropriate algebraic techniques to find $\tan \theta$ and $\theta$.
| \begin{aligned}\tan \theta(\tan\theta +1)&=0\\\tan \theta = 0,\tan \theta &+ 1=0 \end{aligned} | |
| \begin{aligned}\tan \theta&= 0\\\theta &=\pi \end{aligned} | \begin{aligned}\tan \theta + 1&= 0\\\tan \theta &= -1\\\theta &= \dfrac{3\pi}{4} \end{aligned} |
This means that through the help of Pythagorean identities, equations like the one we’ve shown are now easier to simplify and solve.
Proving Trigonometric Identities Using Pythagorean Identities
The reason why Pythagorean identities are important is that they lead to a wide range of other trigonometric identities and properties. Knowing how to simplify, derive and even prove identities using Pythagorean identities is essential, especially when advancing to other trigonometry and math topics.
\begin{aligned}\cos^2\theta &= (1 – \sin \theta)(1 +\sin\theta)\end{aligned}
Simplify the right-hand side of the equation by applying algebraic techniques learned in the past.
\begin{aligned}\cos^2\theta&= (1 – \sin \theta)(1 +\sin\theta)\\&= 1^2 – (\sin \theta)^2\\&= 1 – \sin^2 \theta\end{aligned}
Does the right-hand side of the equation now look familiar?
If we rewrite the Pythagorean identity $\sin^2\theta + \cos^2\theta = 1$, we can show that $1 – \sin^2\theta = \cos^2\theta$.
\begin{aligned}\cos^2\theta &= 1 – \sin^2\\&= \cos^2\theta \end{aligned}
This shows how important Pythagorean identities are when simplifying and proving trigonometric expressions and identities. When you’re ready, head on over to the next section to solve more problems!
Example 1
Suppose that $\sec \theta = -\dfrac{29}{20}$, what is the exact value of $\tan \theta$ if it is also negative?
Solution
We want to find $\tan \theta$’s value given the value of $\sec\theta$. Use the Pythagorean identity $\tan^2\theta + 1= \sec^2\theta$ and the fact that $\sec \theta = -\dfrac{29}{20}$.
\begin{aligned}\tan^2\theta + 1= \sec^2\theta\\ \tan^2\theta + 1&= {\color{DarkOrange}\left(-\dfrac{29}{20}\right)}^2\\\tan^2\theta +1 &= \dfrac{841}{400}\\\tan^2\theta &=\dfrac{441}{400}\\\tan \theta &= \pm \dfrac{21}{20}\end{aligned}
Since we know that $\tan \theta$ is negative, we let go of the positive solution. This means that we have $\tan \theta=-\dfrac{21}{20}$.
Example 2
If $\csc \theta – \cot \theta = -4$, what is the value of $\csc \theta + \cot \theta$?
Solution
Since we’re working with cosecant and cotangent functions, it’s best to focus on the third Pythagorean identity, $1+ \cot^2\theta = \csc^2\theta$. Rewrite this identity so that we can isolate $1$ on the right-hand side of the equation.
\begin{aligned}1+ \cot^2\theta &= \csc^2\theta\\\csc^2\theta – \cot^2\theta &= 1\\(\csc \theta – \cot \theta)(\csc \theta + \cot \theta) &= 1\end{aligned}
Notice anything familiar on the left-hand side of the resulting equation? We now have the expression that’s given in the problem and we have the expression we need to find as well.
\begin{aligned}(\csc \theta – \cot \theta)(\csc \theta + \cot \theta) &= 1\\({\color{DarkOrange}-4})(\csc \theta + \cot \theta)&= 1\\\csc \theta + \cot \theta &= – \dfrac{1}{4}\end{aligned}
This means that $\csc \theta + \cot \theta$ is equal to $-\dfrac{1}{4}$.
Example 3
Show that the trigonometric identity $\tan\theta -\tan\theta\sec^2\theta = \tan^3 \theta$ is true.
Solution
First, let’s factor our $\tan \theta$ from each of the terms on the left-hand side of the equation.
\begin{aligned}\tan\theta -\tan\theta\sec^2\theta = \tan^3 \theta\\\tan\theta(1- \sec^2\theta )= \tan^3 \theta\end{aligned}
We’re working with $\sec^2 \theta$ and $\tan \theta$, so the best Pythagorean identity to use is $\tan^2 \theta +1 = \sec^2\theta$. Rewrite $1 – \sec^2\theta$ in terms of $\tan \theta$ to simplify the left-hand side of the equation.
\begin{aligned}\tan\theta({\color{DarkOrange}\tan^2\theta})&= \tan^3 \theta\\\tan^3\theta &= \tan^3\theta \,\checkmark\end{aligned}
This confirms that $\tan\theta -\tan\theta\sec^2\theta = \tan^3 \theta$ is true.
Practice Questions
1. If $\sin \theta\cos\theta = \dfrac{1}{4}$, what is the value of $\sin \theta – \cos \theta$?
A. $\dfrac{\sqrt{2}}{2}$
B. $\dfrac{\sqrt{3}}{2}$
C. $\dfrac{1}{2}$
D. $\dfrac{3}{2}$
2. Suppose that $\cos \theta = \dfrac{3}{7}$ and $\cot^2 \theta = \dfrac{a}{b}$, what is the value of $a + b$?
A. $31$
B. $40$
C. $49$
D. $98$
3. Which of the following is equivalent to $\dfrac{\cos \theta}{1 + \sin \theta}$?
A. $-\dfrac{1}{\sin \theta \cot \theta}$
B. $\dfrac{1 – \sin \theta}{\sin \theta \cot \theta}$
C. $\dfrac{1 + \sin \theta}{\sin \theta \cot \theta}$
D. $\dfrac{1}{\sin \theta \cot \theta}$
Answer Key
1. A
2. C
3. B
