Obtuse Angle – Explanation and Examples

An obtuse angle is an angle larger than a ninety degree angle and less than a straight line.

Using degrees, an obtuse angle is greater than $90$ degrees and less than $180$ degrees. In radians, an obtuse angle measures more than $\frac{\pi}{2}$ radians and less than $\pi$ radians.

Before moving on with this section, make sure to review angle types and their properties.

This section covers:

• What is an Obtuse Angle?
• Obtuse Angle Definition
• Obtuse Angle Examples

What is An Obtuse Angle?

An obtuse angle is larger than a right angle and smaller than a straight line.

Using degrees, an obtuse angle has a degree measure greater than $90$ and less than $180$. In radians, its measure is between $\frac{\pi}{2}$ and $\pi$.

Sometimes, any angle greater than a right angle is considered obtuse. Angles greater than straight lines and less than a circle are also considered reflex angles. This section will make this distinction.

Obtuse Triangles

One reason to make this distinction is the definition of an obtuse triangle.

Recall that there are three types of triangle angle arrangements. Acute triangles have only angles less than a right angle and right triangles have one right angle.

An obtuse triangle, however, is a triangle with an angle greater than a right angle. Since triangles have a total interior angle measure of $180$ degrees, they can have at most one angle greater than a right angle and no angles greater than a straight line (greater than an obtuse angle).

This is also another reason to distinguish obtuse angles and reflex angles. That is, there cannot be a reflex triangle.

Obtuse Angle Definition

An obtuse angle is an angle greater than a right angle and less than a straight line. It has a measure between $90$ and $180$ degrees or between $\frac{\pi}{2}$ and $\pi$ radians.

Alternatively, an obtuse angle is any largest angle in an obtuse triangle.

Obtuse Angle Examples

Since obtuse angles include any angles with measures greater than $90$ degrees and less than $180$ degrees, examples include angles with measures of:

• 90.0001 degrees
• 100 degrees
• 120 degrees
• 145 degrees
• 175 degrees
• 179.999 degrees

Alternatively, since obtuse angles include any angle with more than $\frac{\pi}{2}$ radians and $\pi$ radians, they include:

• $\frac{3}{4}\pi$ radians
• $\frac{3}{5} \pi$ radians
• $\frac{4}{5} \pi$ radians
• $\frac{9}{10} \pi$ radians

Common Examples

This section covers common examples of problems involving obtuse angles and their step-by-step solutions.

Example 1

Classify the following angles given the degree or radian measure.

A. $91$ degrees

B. $360-50$ degrees

C. $\frac{99}{100}\pi$

D. $\frac{145}{131}\pi$

Solution

The first and third angle measures are measures of an obtuse angle. The second and fourth, however, are not. Specifically, both of them are reflexive angles, or angles greater than a straight line but less than a circle.

The main test is to see whether the given angles are between $90$ and $180$ degrees or between $\frac{\pi}{2}$ radians.

Clearly, $91>90$ and $91<180$, so the first angle is indeed obtuse. The next angle, however, is equal to $310$ degrees. Since $310>180$, this angle is not obtuse. Instead, it is reflexive.

Similarly, $\frac{99}{100}\pi$ is less than $\pi$ and greater than $\frac{pi}{2}$. Therefore, this angle is obtuse.

The next one, however, is $\pi$ multiplied by $\frac{145}{131}$. Since $145>131$, this fraction is greater than one. Therefore, $\frac{145}{131}\pi$ is greater than $\pi$. This makes the angle not obtuse and instead reflexive.

Example 2

Let a triangle $ABC$ have two known angles measuring $41$ and $31$ degrees. Is the triangle obtuse? Why or why not?

Solution

Recall that triangles have an interior angle measure of $180$ degrees. Therefore, given these two angle measures, it is possible to determine the measure of the third angle.

That is, the angle will be equal to $180-(41+31)=180-72=108$. Since $90<108<180$, this angle is obtuse. Therefore, the triangle $ABC$ is obtuse.

Example 3

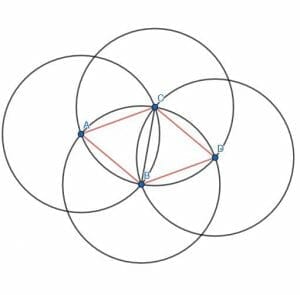
Prove that the angle $ACD$ in the figure $ACDB$ is obtuse.

Solution

Begin by noting that the triangles $ABC$ and $CBD$ are congruent equilateral triangles.

Why?

$AC$ is a radius of the circle with center $A$, as is $AB$. $AB$ is also a radius of the circle with center at $B$, and $BC$ is another radius of this circle. Therefore, $ABC$ is equilateral.

Similarly, $BC$ and $BD$ are both radii of the same circle centered at $B$. The line $BD$ is also a radius of the circle centered at $E$, and so is $DC$. Therefore, $CB$, $BD$, and $DC$ are all lines with the same length. Thus, $CBD$ is also equilateral.

But, the two triangles have a common side, $CB$. Therefore, all of the sides are the same length.

Consequently, then, the angle $ACB$ must be equal to $60$ degrees as must the angle $DCB$.

Since the angle in question, $ACD$, is comprised of the angles $ACB$ and $DCB$ together, the measure of $ACD$ is equal to $ACB + DCB = 60 + 60 = 120$ degrees.

Therefore, since $120$ is greater than $90$ degrees but less than $180$ degrees, the angle $ACD$ is obtuse.

Example 4

Prove that the interior angles of any regular n-gon with $n>4$ has only obtuse angles.

Solution

This problem primarily relies on knowing that an n-gon has a total interior angle sum of $180(n-2)$.

When such a polygon is a regular polygon, it has $n$ equal interior angles. Therefore, each interior angle has a measure of $\frac{180n-360}{n}$ or $180-\frac{360}{n}$.

For any positive $n$, $180-\frac{360}{n}$ is less than $180$. Now it is required to prove that for any $n>4$, $180-\frac{360}{n}>90$.

For this to be true, $\frac{360}{n}$ must be less than $90$. If it is greater than or equal to $90$, then subtracting it from $180$ results in a degree measure less than or equal to $90$, meaning such angles are either right or acute.

If

$\frac{360}{n} < 90$,

then:

$360 < 90n$

Dividing by $90$ yields:

$4 < n$.

Therefore, when $n > 4$, the interior angles of any regular polygon are all between $90$ and $180$ and are consequently obtuse angles.

Example 5

Two angles make up a circle. One of the angles is obtuse. What is the range of degree and radian values for the second angle?

Solution

Recall that supplementary angles are angles which, when put together, make a straight line. That is, their sum is $180$ degrees or $\pi$ radians.

An angle which, when put together with an obtuse angle, makes a circle will be the sum of a straight line and the angle supplementary to the obtuse angle.

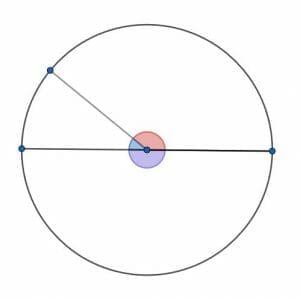
If the red angle is the given obtuse angle, then the angle which completes the circle is the purple straight angle with the blue angle which is supplementary to the red angle.

Therefore, it is necessary to first find the range of values for supplementary angles for obtuse angles. Since the obtuse angle is greater than $90$, the supplementary angle is less than $180-90 = 90$.

Similarly, since the obtuse angle is less than $180$ degrees, the supplementary angle is greater than $180-180 = 0$.

Thus, the supplementary angle is any acute angle, or any angle between $0$ and $90$ degrees. In radians, this is between $0$ and $\frac{\pi}{2}$ radians.

But, this is not the angle needed to create the circle. This angle plus a straight angle makes the needed angle. Therefore, the needed angle will be an acute angle plus a straight angle or an angle greater than $180$ degrees but less than $180+90 = 270$ degrees.

In radians, this is an angle greater than $\pi$ radians and smaller than $\frac{3\pi}{2}$ radians.

More Examples with Explanation

1. Prove that two obtuse angles must create a reflexive angle.
2. Consider an obtuse isosceles triangle. What are the minimum and maximum measures of its two base angles? Give the answer in both radians and degrees.
3. A circle is divided into three obtuse angles. At least two of the angles have the same measure. What is the range of possible measures for the third angle? Give the answer in both radians and degrees.
4. Prove that if the exterior angle of a polygon is obtuse, then the polygon must be concave.
5. Prove that a triangle cannot be both right and obtuse at the same time.

Answer Key

1. A reflexive angle has a measure greater than a straight line but less than a complete circle. Since obtuse angles must be greater than a right angle, two obtuse angles together must be greater than two right angles. But, two right angles is a straight line. Therefore, the sum of two obtuse angles is greater than a straight line.
   Similarly, since each obtuse angle must be less than a straight line, two obtuse angles must be less than two straight lines, which is equivalent to a circle. Therefore, the sum of the two obtuse angles is greater than a straight line but less than a circle, meaning it is a reflexive angle.
2. The range is $0 < \alpha < \frac{180-90}{2} = 45$ degrees or $0 < \alpha < \frac{\pi-\frac{\pi}{2}}{2} = \frac{\pi}{4}$ for some angle $\alpha$.
3. First, find the range of the sum of the two obtuse angles. This was done in the first problem. The range is, consequently, greater than $180$ degrees and less than $360$ degrees.
   But, the third angle must also be obtuse. That is, it must be less than $180$ degrees but more than $90$ degrees. Therefore, the sum of the two equal angles must be less than $360-90 = 270$. Thus, the maximum value of the angles individually is less than $\frac{270}{2} = 135$ degrees.
   In radians, this is $\frac{\frac{3\pi}{2}}{2} = \frac{3\pi}{4}$.
4. A concave polygon has at least one angle greater than a straight line. The corresponding exterior angle for any angle, $\beta$ in a polygon will be $360-\beta$. As proved in example 5, $360$ minus any obtuse angle will be a reflexive angle greater than a straight line.
   Thus, if an exterior angle is obtuse, the interior angle must be reflexive and greater than a straight line. Therefore, such a polygon is concave.
5. Prove this by contradiction. Suppose a triangle was both right and obtuse. Then, such a triangle has a $90$ degree angle and an angle greater than $90$ degrees. Therefore, the sum of the angles in the triangle is greater than $90+90 = 180$.
   But, the sum of the angles in a triangle must equal $180$. Therefore, such a triangle cannot exist.

Images/mathematical drawings are created with GeoGebra.