- Home
- >
- Number Properties – Definition & Examples
JUMP TO TOPIC
Number Properties – Definition & Examples
 To count a certain quantity, we use a mathematical object called number. Each number is represented by symbols, called numerals. For example, the number eight is represented by a numeral 8.
To count a certain quantity, we use a mathematical object called number. Each number is represented by symbols, called numerals. For example, the number eight is represented by a numeral 8.
A particular number can be either positive or negative. These are called signed numbers. If no sign is shown with the number, it is by-default considered as positive. On the number line, the numbers to the right of 0 are positive and the numbers to the left of 0 are negative.
An absolute value is a magnitude of a signed number. Whether the number is negative or positive, the absolute value is always positive.
Operations with Signed Numbers
Numbers are also used in making calculations. You can perform all arithmetic operations on numbers, for example, addition, subtraction, multiplication, and division. These operations are applied to the absolute values of the signed numbers.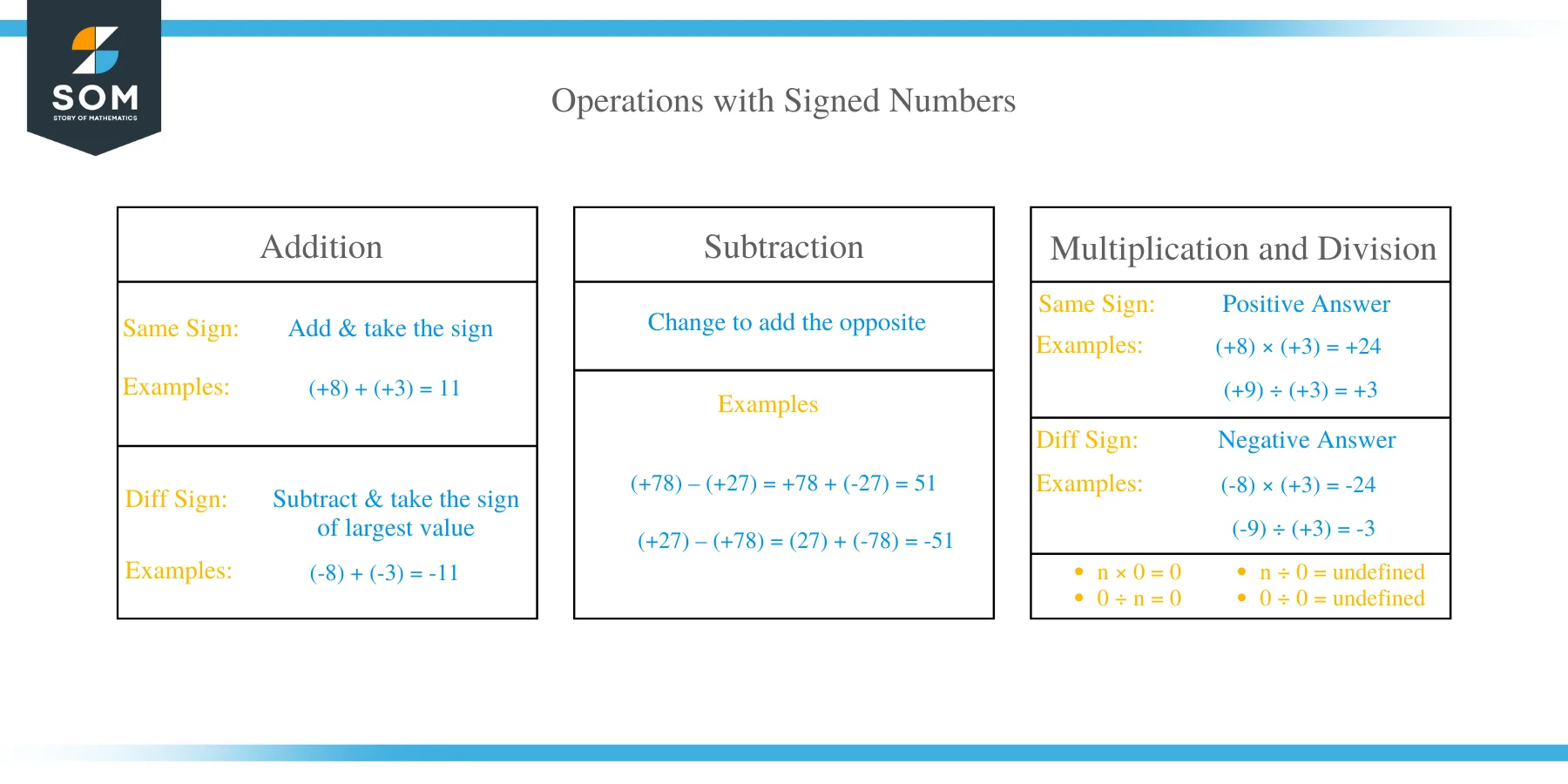
Addition of Signed Numbers
To add the two signed numbers of the same type (either both positive or both negative), you just need to add the absolute values and keep the original sign with the result.
Example 1
Add the following:
+8 + (+3)
- Step 1: Add the absolution values,
8 + 3 = 11
- Step 2: Keep the original sign,
+11
Example 2
Add the following:
-8 + (-3)
- Step 1: Add the absolution values,
8 + 3 = 11
- Step 2: Keep the original sign,
-11
To add the two signed numbers of different type (one positive and one negative), you just need to subtract the absolute values and keep with the result the sign of the number which has the larger absolute value.
Example 3
Add the following:
+8 + (-3)
- Step 1: Subtract the absolution values,
8 – 3 = 5
- Step 2: Keep with the result the sign of the number which has the larger absolute value (+8).
+5
Example 4
Add the following:
-8 + (+3)
- Step 1: Subtract the absolution values,
8 – 3 = 5
- Step 2: Keep with the result the sign of the number which has the larger absolute value (-8).
-5
Subtraction of Signed Numbers
To subtract the two signed numbers, you only need to change the sign of the number which is getting subtracted and then add both numbers together.
Example 5
Subtract the following:
+78 – (+27)
- Step 1: Change the sign of the number which is getting subtracted,
+78 + (-27)
- Step 2: Add both numbers,
51
Keep with the result the sign of the number which has the larger absolute value (78).
+51
Example 6
Subtract the following:
+27 – (+78)
- Step 1: Change the sign of the number which is getting subtracted,
+27 + (-78)
- Step 2: Add both numbers,
51
Keep with the result the sign of the number which has the larger absolute value (-78).
-51
Multiplication and Division of Signed Numbers
Multiplication and division of signed numbers is same like that of regular numbers, just you need to take care of the signs. The positive signs do not cause any mess, as result is always positive when signs of all numbers are positive, but if there is negative sign(s) somewhere, the result can be either positive or negative. If there are even number of negative signs, then the result is positive. If there are odd number of negative signs, then the result is negative.
Note that if any number is multiplied by zero, the result is zero i.e.
9 × 0 = 0
Similarly, if zero is divided by any signed number then the result is zero. If any signed number or zero is divided by zero then the result is undefined i.e.
0/9 = 0
9/0 = undefined
0/0 = undefined
Example 7
Multiply the following:
(-6) (+3) (-1) (-2) (+2)
- Step 1: Simply multiply the absolution values of all numbers,
(6) (3) (1) (2) (2) = 72
- Step 2: State the number of negative signs,
3 (odd)
Step 3: State the final answer,
-72
Example 8
Divide the following:
(-9) (+10) (-12) ÷ (-5) (-4) (+3)
- Step 1: Simply divide the absolution values of all numbers; 9 is divisible by 3, 10 is divisible by 5, and 12 is divisible by 4.
(3) (2) (3) = 18
- Step 2: State the number of negative signs,
4 (even)
- Step 3: State the final answer,
+18
Rules of Signed Numbers
When there is more than one arithmetic operation in the expression, you need to follow the certain rules. A simple problem can include, parentheses, signed numbers, exponents, plus sign, minus sign, multiplications sign, and division sign. You cannot simply apply the operations randomly.
There is a phrase ‘PEMDAS’ which tells you about the order of operation:
P: Parenthesis
E: Exponents
M: Multiplication
D: Division
A: Addition
S: Subtraction
This means you need to solve the expression inside the parentheses first. When done with parenthesis, look for the exponents and evaluate. Then you need to perform all multiplication and division operations. In the last, you will go for addition and subtraction from left to right.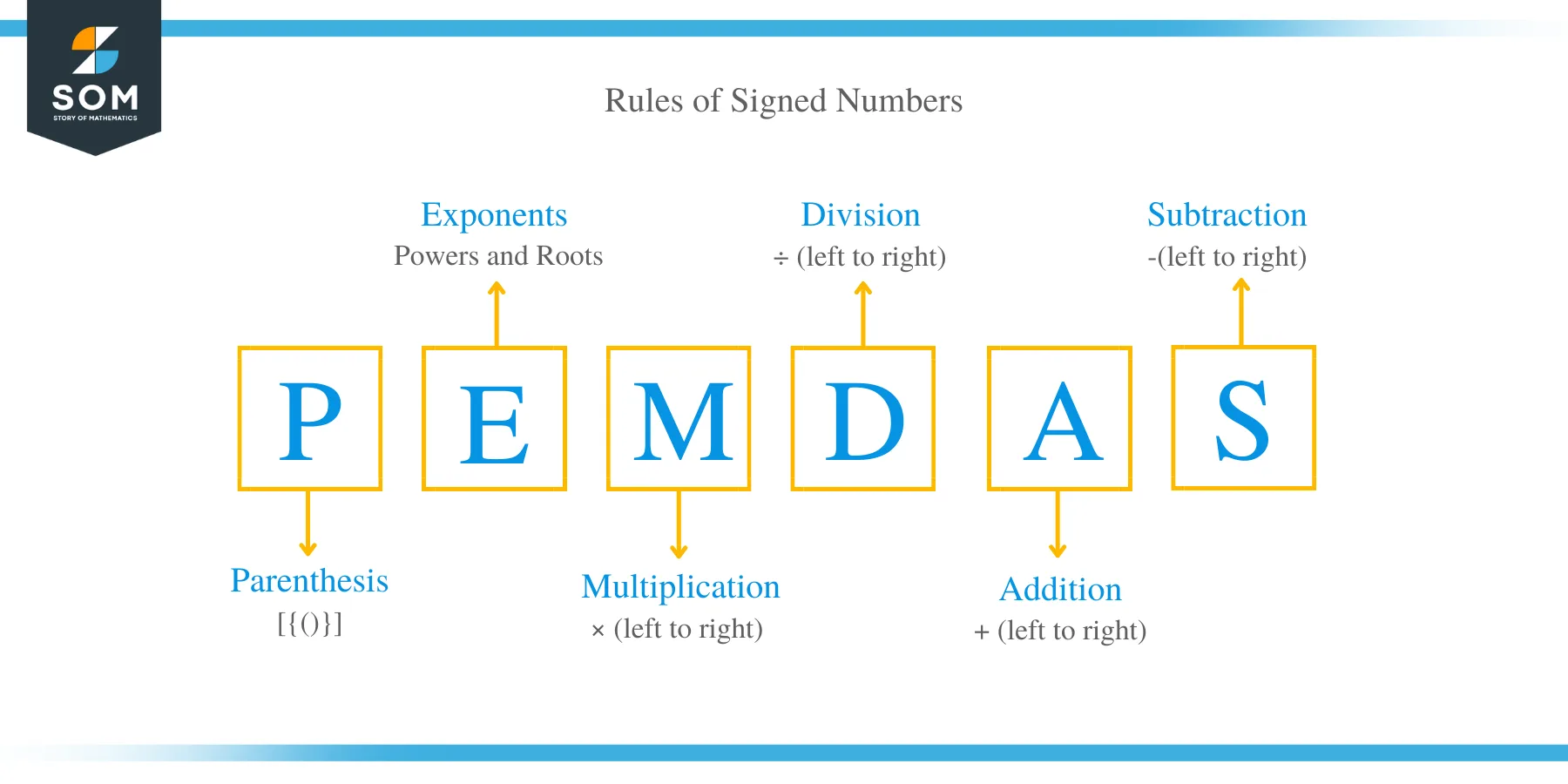
Example 9
Solve
(3 + 9) × 24 – 5 ÷ 2.5
- Step 1: Solve the parenthesis first
12 × 24 – 5 ÷ 2.5
- Step 2: Solve the exponent.
12 × 16 – 5 ÷ 2.5
- Step 3: Multiplication.
192 – 5 ÷ 2.5
- Step 4: Division
192 – 2
- Step 5: Subtraction.
190
Summary
Summarizing the operations and rules of signed numbers in the tabular form below:
| Problem | Operation | Sign of Result |
| Positive Number + Positive Number | Addition | Positive |
| Negative Number + Negative Number | Addition | Negative |
| Positive Number + Negative Number | Subtraction | Keep with the result the sign of the number which has the larger absolute value. |
| Negative Number – Negative Number | Subtraction | Same rule applies for the signed number with addition. |
| Positive Number – Negative Number | ||
| Positive Number – Positive Number | ||
| Positive Number × Positive Number | Multiplication | Positive |
| Negative Number × Negative Number | Multiplication | Positive |
| Positive Number × Negative Number | Multiplication | Negative |
| Positive Number ÷ Positive Number | Division | Positive |
| Negative Number ÷ Negative Number | Division | Positive |
| Positive Number ÷ Negative Number | Division | Negative |
