• Home
  • >
  • Multiplying Mixed Numbers – Methods & Examples

Multiplying Mixed Numbers – Methods & Examples

Multiplying Mixed NumbersA mixed number is a number that contains a whole number and a fraction, for instance 2 ½ is a mixed number.

How to Multiply Mixed Numbers?

Mixed numbers can be multiplied by first converting them to improper fractions. For example, 2 ½ can be converted to 5/2 before the multiplication process. Below are the general rules for multiplying mixed numbers:

  • Convert the mixed numbers to improper fractions first.
  • Multiply the numerators from each fraction to each other and place the product at the top.
  • Multiply the denominators of each fraction by each other (the numbers on the bottom). The product is the denominator of the new fraction.
  • Simplify or reduce the final answer to the lowest terms possible.


Multiplying Mixed Fractions and Mixed Numbers


One method of multiplying mixed fractions is to convert them to improper fractions.

Example 1

3 1/8 x 2 2/3

Solution

  • Convert each fraction to an improper fraction,

3 1/8 = {(3 x 8) +}/ 8 = 25/8
2 2/3 = {(2 x 3) + 2}/3 = 8/3

  • Multiply the numerator and denominators,

25/8 x 8/3 = ( 25 x 8)/(8 x 3)

  • In this case, common factors are at the top and bottom, therefore, simplify by cancellations,

= 25/3

  • Convert the final answer to mixed fractions,

25/3 = 8 1/3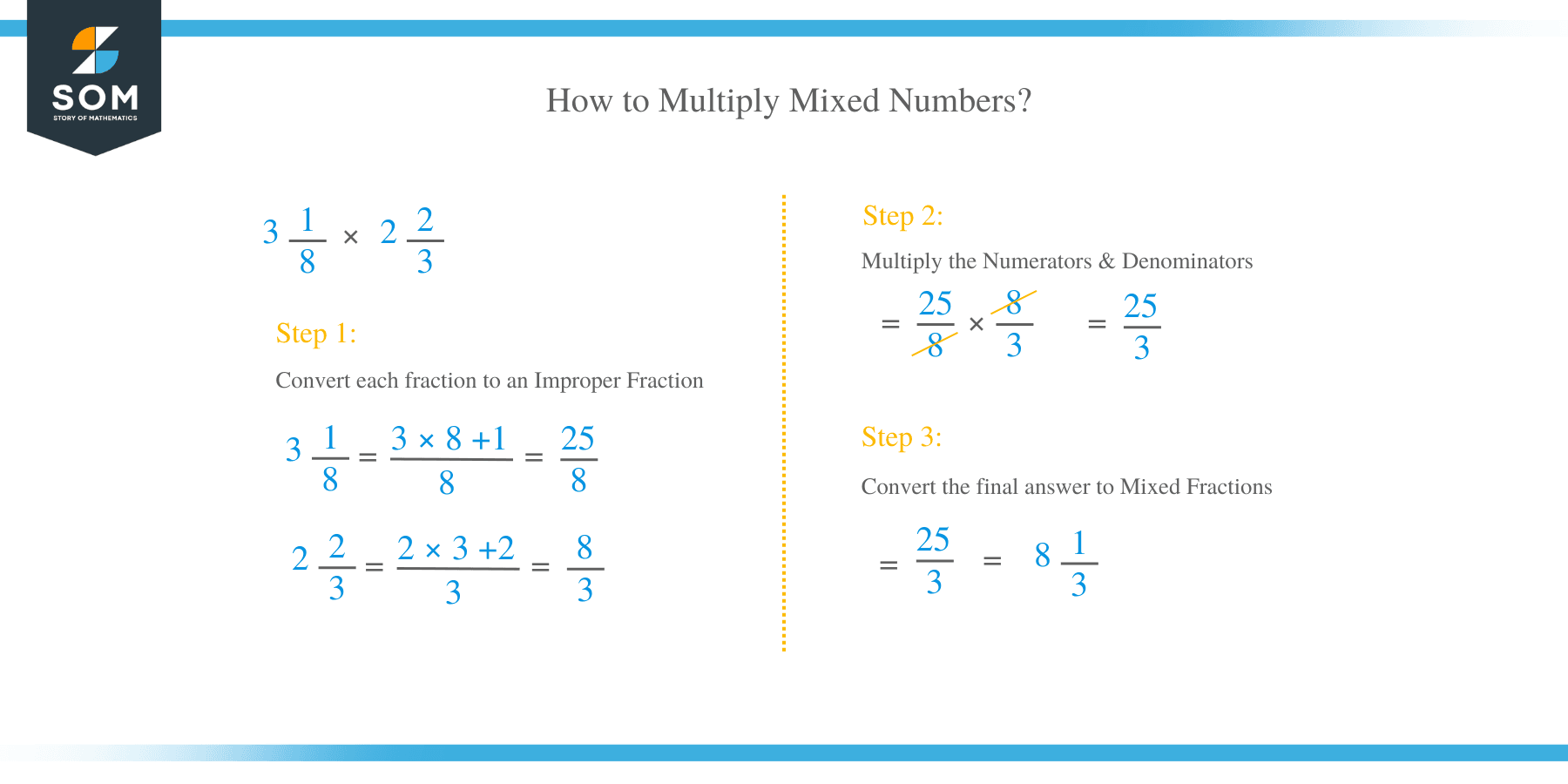How to Multiply Mixed Numbers?

Example 2

1 4/5 x 5 3/8

Solution

  • First change the mixed numbers to improper fractions

1 4/5 = (1 x 5 + 4)/5 = 9/5

5 3/8 = (8 x 5 +3)/8 = 43/8

  • Multiply the fractions

9/5 x 43/8 = 387/40

  • You either the answer as an improper fraction or convert it to a mixed number

387/40 = 9 27/40

Area Model Method

Multiplication of mixed numbers can also be done using another method called area model. This method is illustrated below:

Example 3

2 2/5 x 3 1/4

Solution

  • Draw a model that has a region for both whole number and fraction number
X22/5
3  
¼  
  • Multiply each row with each column
X22/5
32 x 3 =63 x 2/5 = 6/5
¼1/4 x 2 = 1/21/4 x 2/5 = 2/20 = 1/10
  • Add all the products in the table.

6 + 1/2 + 6/5 + 1/10

  • Add the fractions

The L.C.M. of 2, 5 and 10 =10

Therefore, 1/2 + 6/5 + 1/10 = 5/10 + 12/10 + 1/10

  • Add the numerators alone while maintaining the denominator

(5 + 12 + 1)/10

= 18/10 = 1 8/10

  • Now add 1 8/10 + 6

= 7 8/10

  • Simplify the fraction to its lowest terms.

= 7 4/5

Practice Questions

1. A woman distributed a fraction of a pineapple among her 6 daughters. If each person got 19 of the pineapple. What is the total fraction of the pineapple that the woman distributed?

2. Edwin and Ann bought 15 kg of sweets at their wedding and distributed 34 of it among the visitors. How many sweets did they distribute?

3. My weight was 60 kg before I lost 110 of the weight in the past 3 months. How much weight did I lose?

4. Jason had $3140 in his bank account. He spent 25 of it to buy essentials from the grocery. How much money did he spend?

5. Stella had 15 liters of milk in a container. If she consumed 34 of the milk. How many liters of milk were consumed?

6. A boy walks 312 kilometers daily. What is the total distance covered in one week?

7. Ahmed read 23 of his storybook having 420 pages. If Mike read 34 of the same storybook, find out who read many pages and how many were they?

8. A rectangular school garden is 645 meters long and 138 meters wide. Which of the following shows the area of the garden?

9. It takes 56 yards of wool to manufacture a dress. How many yards of wool is needed to make 8 similar dresses?

10. A bike ride rode for 437 kilometers on Friday. He rode 8 times more distance on Saturday than he did on Friday. How many kilometers were covered on Saturday?


 

Previous Lesson | Main Page | Next Lesson