Matrix Multiplication – Explanation & Examples

There are $ 3 $ general operations on matrices. These are:

• Matrix Addition
• Matrix Subtraction
• Matrix Multiplication

Matrix addition and matrix subtraction are easy operations. You can read more about matrix addition here and more about matrix subtraction here.

Matrix multiplication is of $ 2 $ types:

• Scalar Multiplication
• Matrix Multiplication

Scalar multiplication is not very complicated and straightforward. Still, matrix multiplication can be a bit intimidating at first. After you read this lesson, it will become as easy as the other operations on matrices.

Let’s take a look at the definition of matrix multiplication:

Matrix multiplication is the operation that involves multiplying a matrix by a scalar or multiplication of $ 2 $ matrices together (after meeting certain conditions).

This lesson will show how to multiply matrices, multiply $ 2 \times 2 $ matrices, multiply $ 3 \times 3 $ matrices, multiply other matrices, and see if matrix multiplication is defined, and some properties of matrix multiplication.

How to Multiply Matrices

To multiply two matrices together, we first need to make sure that the number of columns of the 1st matrix is equal to the number of rows of the 2nd matrix. If they aren’t equal, then matrix multiplication is undefined.

If they are equal, we can multiply the $ 2 $ matrices together. The resulting matrix will have a dimension equal to the number of rows of the 1st matrix and the number of columns of the 2nd matrix.

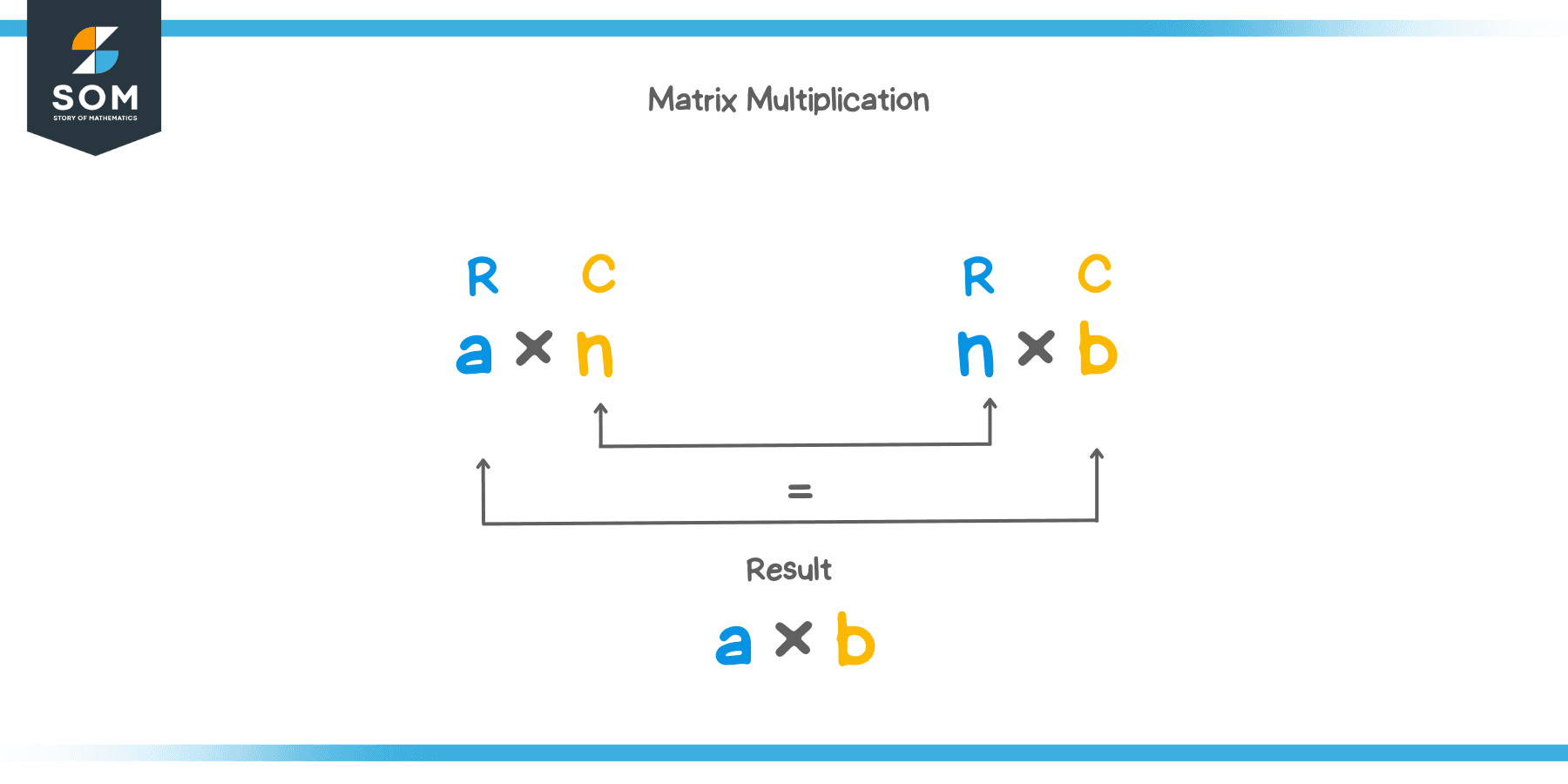
If the first matrix has a dimension of $ a \times b $ and the second matrix’s dimension is $ m \times n $, for matrix multiplication to be defined, the number of columns of the first matrix ($ b $) must equal the number of rows of the second matrix ($ m $). The resultant matrix will have dimensions $ a \times n $.

To multiply $ 2 $ matrices, we need to understand the dot product. Consider the two $ 1 \times 3 $ matrices shown below:

$  \begin{bmatrix} { 1 }  & { 2 } & 1  \end {bmatrix} $

$ \begin{bmatrix} { 2 }  & { 0 } & 4  \end {bmatrix} $

To take its dot product, we multiply each corresponding entry of the $ 2 $ matrices with each other and take the sum. Shown below:

$ = (1)(2) + (2)(0) + (1)(4) = 2 + 0 + 4 = 6 $

Note that the dot product is a number only! Remember, for a dot product to exist, both the matrices have to have the same number of entries! Hence, the number of columns of the first matrix must equal the number of rows of the second matrix when we are multiplying $ 2 $ matrices. We will see it shortly.

Steps to multiply two matrices

1. Check whether the number of columns of the first matrix is equal to the second matrix’s number of rows. If so, we can perform matrix multiplication. If not, the operation is undefined. Note the resultant matrix will have a dimension equal to the row number of the first matrix and column number of the second matrix.
2. Take the dot product of the first row of the first matrix with the first column of the second matrix. Put the answer in the first row, first column placeholder in the resultant matrix.
3. Take the dot product of the first row of the first matrix with the second column of the second matrix. Put the answer in the first row, second column placeholder in the resultant matrix.
4. Continue this process until all the rows and columns of both the matrices are exhausted. The resulting matrix is your answer. Remember a general rule, if you’re multiplying the $ n^{th} $ row with the $m^{th} $ column, remember to put the answer in the $ n^{th} $ row,  $m^{th} $ column of the resultant matrix.

How to Multiply 2 x 2 Matrices

Consider Matrix $ A $ and Matrix $ B $ shown below:

$  A = \begin{bmatrix} { 1 }  & { 3 } \\ 1 & { – 2 }  \end {bmatrix} $

$  B = \begin{bmatrix} { 0 }  & { – 3 } \\ 1 & { 1 }  \end {bmatrix} $

Both Matrix $ A $ and $ B $ are $ 2 \times 2 $ matrices. We will follow the steps outlined above to perform the multiplication between Matrix $ A $ and Matrix $ B $. Since the column number of the first matrix is equal to the row number of the second matrix, we can go ahead and perform the multiplication. The process is shown below:

$ A \times B = \begin{bmatrix} { 1 }  & { 3 } \\ 1 & { – 2 }  \end {bmatrix} \times \begin{bmatrix} { 0 }  & { – 3 } \\ 1 & { 1 }  \end {bmatrix} $

$ =\begin{bmatrix} { (1)(0) + (3)(1) }  & { (1)(-3) + (3)(1) } \\ { (1)(0) + (- 2 )(1)} & { (1)(-3) + (-2)(1) }  \end {bmatrix} $

$ =\begin{bmatrix} { 3 }  & { 0 } \\ { – 2 } & { – 5 }  \end {bmatrix} $

Thus,

$ A \times B =\begin{bmatrix} { 3 }  & { 0 } \\ { – 2 } & { – 5 }  \end {bmatrix} $

The process of multiplying $ 3 \times 3 $ matrices is similar. We will look at it below.

How to Multiply 3 x 3 Matrices

Consider Matrix $ A $ and Matrix $ B $ shown below:

$  A = \begin{bmatrix} { 1 }  & { 3 } & { – 1 } \\ 1 & { – 2 } & 0 \\ 1 & { – 1 } & 2  \end {bmatrix} $

$  B = \begin{bmatrix} { – 2 }  & { 6 } & { 0 } \\ 1 & { – 5 } & 1 \\ 0 & { – 1 } & { – 4 }  \end {bmatrix} $

Both Matrix $ A $ and $ B $ are $ 3 \times 3 $ matrices. We will follow the steps outlined above to perform the multiplication between Matrix $ A $ and Matrix $ B $. Since the column number of the first matrix is equal to the row number of the second matrix, we can go ahead and perform the multiplication. The process is shown below:

$ A \times B = \begin{bmatrix} { 1 }  & { 3 } & { – 1 } \\ 1 & { – 2 } & 0 \\ 1 & { – 1 } & 2  \end {bmatrix} \times \begin{bmatrix} { – 2 }  & { 6 } & { 0 } \\ 1 & { – 5 } & 1 \\ 0 & { – 1 } & { – 4 }  \end {bmatrix} $

$ =\begin{bmatrix} { (1)(-2) + (3)(1) + (-1)(0) }  & { (1)(6) + (3)(-5) + (-1)(-1) } & { (1)(0) + (3)(1) + (-1)(-4) } \\ { (1)(-2) + (-2)(1) + (0)(0) } & { (1)(6) + (-2)(-5) + (0)(-1) } & { (1)(0) + (-2)(1) + (0)(-4) } \\ {(1)(-2) + (-1)(1) + (2)(0)} & { (1)(6) + (-1)(-5) + (2)(-1) } & {(1)(0) + (-1)(1) + (2)(-4) }  \end {bmatrix} $

$ =\begin{bmatrix} { 1 }  & { – 8 } & { 7 } \\ { – 4 } & { 16 } & { – 2 } \\ { – 3 } & {9} & { – 9 }  \end {bmatrix} $

Thus,

$ A \times B =\begin{bmatrix} { 1 }  & { – 8 } & { 7 } \\ { – 4 } & { 16 } & { – 2 } \\ { – 3 } & {9} & { – 9 }  \end {bmatrix} $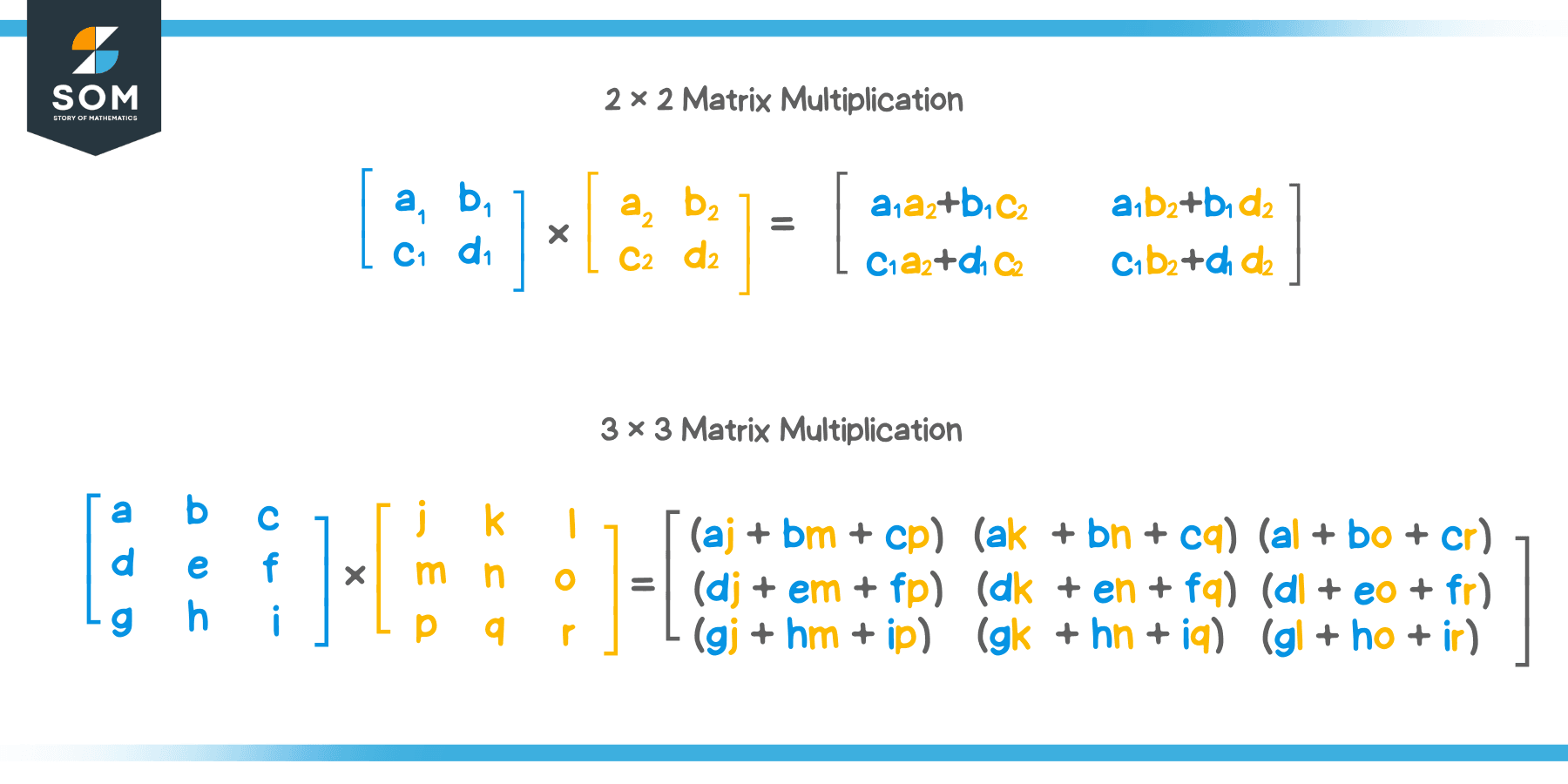

Multiplying Matrices with Different Dimensions

We have looked at only square matrix multiplication (e.g. $ 2 \times 2 $ matrix with another $ 2 \times 2$ matrix and $3 \times 3$ matrix with another $3 \times 3$ matrix).

What if both the matrices to be multiplied are not the same order?

Not a problem! Just check if the the number of columns of the first matrix is equal to the number of rows of the second matrix. If they are, we follow the steps outlined above and multiply the $ 2 $ matrices. Also, remember that the resultant matrix dimension would be $ a \times n $, where $ a $ is the number of rows of the first matrix and $ n $ is the number of columns of the second matrix. We will look at an example later on.

Matrix Multiplication Rules

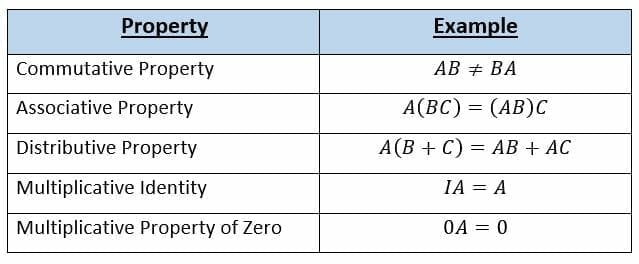
We will look at $ 5 $ properties of matrix multiplication. They are outlined in the table shown below ($ A $ and $ B $ are $ n \times n $ matrices, $ I $ is the $ n \times n $ identity matrix, and $ 0 $ is the $ n \times n $ zero matrix):

Now, let us see some examples to clarify our understanding of Matrix Multiplication.

Example 1

Comment whether the following matrices can be multiplied or not. If so, what will be the dimension of the resultant matrix?

1. $ 2 \times 2 $ matrix with another $ 2 \times 2 $ matrix
2. $ 1 \times 4 $ matrix with a $ 4 \times 1 $ matrix
3. $ 3 \times 3 $ matrix with a $ 2 \times 3 $ matrix

Solution

Recall that if the column number of the first matrix is equal to the second matrix’s row number, the two matrices can be multiplied. The resultant matrix will have dimension $ a \times b $ where $ a $ is the number of rows of the first matrix and $ b $ is the number of columns of the second matrix.

1. Yes, both the matrices can be multiplied and the resulting matrix will have dimension $ 2 \times 2 $.
2. Yes, both of these matrices can be multiplied and the resulting matrix will be of the order 1. It will be a $ 1 \times 1$ matrix.
3. No, these two matrices can’t be multiplied since the number of columns of the first matrix ($3$) is not equal to the number of rows of the second matrix ($2$). Matrix multiplication between these $2$ matrices is undefined.

Example 2

Multiply Matrix $ A $ and Matrix $ B $ shown below:

$  A = \begin{bmatrix} { 0 }  & { – 3 } \\ 2 & { 0 }  \end {bmatrix} $

$  B = \begin{bmatrix} { 1 }  & { 1 } \\ 5 & { – 2 }  \end {bmatrix} $

Solution

Both matrix $ A $ and $ B $ are $ 2 \times 2 $ matrices. Since the column number of the first matrix is equal to the row number of the second matrix, we can go ahead and perform the multiplication. The process is shown below:

$ A \times B = \begin{bmatrix} { 0 }  & { – 3 } \\ 2 & { 0 }  \end {bmatrix} \times \begin{bmatrix} { 1 }  & { 1 } \\ 5 & { – 2 }  \end {bmatrix} $

$ =\begin{bmatrix} { (0)(1) + (-3)(5) }  & { (0)(1) + (-3)(-2) } \\ { (2)(1) + (0 )(5)} & { (2)(1) + (0)(-2) }  \end {bmatrix} $

$ =\begin{bmatrix} { -15 }  & { 6 } \\ { 2 } & { 2 }  \end {bmatrix} $

Example 3

Multiply  the matrix $ \begin{bmatrix} { 3 }  & { 2 } \\ { 1 } & { -4 }  \end {bmatrix} $ with the $ 2 \times 2 $ identity matrix. Which property of matrix multiplication does it illustrate?

Solution

Let’s perform the indicated multiplication using matrix multiplication rules:

$  \begin{bmatrix} { 3 }  & { 2 } \\ { 1 } & { -4 }  \end {bmatrix} \times \begin{bmatrix} { 1 }  & { 0 } \\ 0 & 1  \end {bmatrix} $

$ =\begin{bmatrix} { (3)(1) + (2)(0) }  & { (3)(0) + (2)(1) } \\ { (1)(1) + (-4 )(0)} & { (1)(0) + (-4)(1) }  \end {bmatrix} $

$ =\begin{bmatrix} { 3}  & { 2 } \\ { 1 } & { -4 }  \end {bmatrix} $

The resultant matrix is equal to the original matrix. This problem illustrated the Multiplicative Identity of matrix multiplication.

Now, it’s your turn to try out some problems.

Practice Questions

1. Comment whether the following matrices can be multiplied or not. If so, what will be the dimension of the resultant matrix?
   
   1. $ 3 \times 1 $ matrix with a $ 1 \times 4 $ matrix
   2. $ 4 \times 4 $ matrix with another $ 4 \times 4 $ matrix
   3. $ 2 \times 4 $ matrix with a $ 3 \times 4 $ matrix
2. For the two matrices shown below, is $ AB = BA $ ?$  A = \begin{bmatrix} { 1 }  & { 0 } \\ 3 & { 0 }  \end {bmatrix} $

   $  B = \begin{bmatrix} { 1 }  & { -1 } \\ 0 & { 1 }  \end {bmatrix} $

3. Multiply Matrix $ C $ and Matrix $ D $ shown below:

   $  C = \begin{bmatrix} { 1 }  & { – 4 } & 1 \\ 1 & 2 & 3 \\ -1 & 2 & -1  \end {bmatrix} $

   $  D = \begin{bmatrix} { 0 }  & 1 & 7\\ 1 & -1 & -1 \\ 1 & { 0 } & 2  \end {bmatrix} $

Answers

1. Recall that if the column number of the first matrix is equal to the second matrix’s row number, the two matrices can be multiplied. The resultant matrix will have dimension $ a \times b $ where $ a $ is the number of rows of the first matrix and $ b $ is the number of columns of the second matrix.
   
   1. Yes, both the matrices can be multiplied and the resulting matrix will have dimension $ 3 \times 4 $.
   2. Yes, both of these matrices can be multiplied and the resulting matrix will be of the order 4. It will be a $ 4 \times 4$ matrix.
   3. No, these two matrices can’t be multiplied since the number of columns of the first matrix ($4$) is not equal to the number of rows of the second matrix ($3$). Matrix multiplication between these $2$ matrices is undefined.
2. First, let’s find $ AB $:$  \begin{bmatrix} { 1 }  & { 0 } \\ 3 & { 0 }  \end {bmatrix} \times \begin{bmatrix} { 1 }  & { -1 } \\ 0 & { 1 }  \end {bmatrix} $

   $ =\begin{bmatrix} { (1)(1) + (0)(0) }  & { (1)(-1) + (0)(1) } \\ { (3)(1) + (0)(0)} & { (3)(-1) + (0)(1) }  \end {bmatrix} $

   $ =\begin{bmatrix} {1}  & {-1} \\ {3} & {-3}  \end {bmatrix} $

   Therefore,
   $ A \times B =\begin{bmatrix} {1}  & {-1} \\ {3} & {-3}  \end {bmatrix} $

   Now, let’s find $ BA $:

   $  \begin{bmatrix} { 1 }  & { -1 } \\ 0 & { 1 }  \end {bmatrix} \times \begin{bmatrix} { 1 }  & { 0 } \\ 3 & { 0 }  \end {bmatrix} $

   $ =\begin{bmatrix} { (1)(1) + (-1)(3) }  & { (1)(0) + (-1)(0) } \\ { (0)(1) + (1)(3)} & { (0)(0) + (1)(0) }  \end {bmatrix} $

   $ =\begin{bmatrix} {-2}  & {0} \\ {3} & {0}  \end {bmatrix} $

   Therefore,
   $ B \times A =\begin{bmatrix} {-2}  & {0} \\ {3} & {0}  \end {bmatrix} $

   Thus, we see that $ AB \neq BA $. Matrix multiplication is not commutative!

    

3. Let’s multiply the two $ 3 \times 3 $ matrices following the matrix multiplication steps. Shown below:$ C \times D = \begin{bmatrix} { 1 }  & { – 4 } & 1 \\ 1 & 2 & 3 \\ -1 & 2 & -1  \end {bmatrix} \times \begin{bmatrix} { 0 }  & 1 & 7\\ 1 & -1 & -1 \\ 1 & { 0 } & 2  \end {bmatrix} $

   $ =\begin{bmatrix} { (1)(0) + (-4)(1) + (1)(1) }  & { (1)(1) + (-4)(-1) + (1)(0) } & { (1)(7) + (-4)(-1) + (1)(2) } \\ { (1)(0) + (2)(1) + (3)(1) } & { (1)(1) + (2)(-1) + (3)(0) } & { (1)(7) + (2)(-1) + (3)(2) } \\ {(-1)(0) + (2)(1) + (-1)(1)} & { (-1)(1) + (2)(-1) + (-1)(0) } & {(-1)(7) + (2)(-1) + (-1)(2) }  \end {bmatrix} $

   $ =\begin{bmatrix} {-3}  & {5} & 13 \\ 5 & {-1} & {11} \\ 1 & {-3} & {-11}  \end {bmatrix} $

   Thus,

   $ C \times D =\begin{bmatrix} {-3}  & {5} & 13 \\ 5 & {-1} & {11} \\ 1 & {-3} & {-11}  \end {bmatrix} $

Previous Lesson | Main Page | Next Lesson