Even or Odd Function Calculator + Online Solver with Free Steps

An Even or Odd Function calculator is an online calculator that helps to determine whether the given function is either even, odd, or neither even nor odd.

The user simply needs to put in the function f(x) and the calculator will do the rest.

The even or odd function calculator helps in checking the parity of the function; whether the given function is odd or even or neither. It identifies the parity of the function by verifying its symmetry. 

The even or odd function calculator makes use of graphical representation in the answer to help the user develop a better understanding of even, odd, and neither even nor odd functions. It also provides the user with a detailed step-by-step solution that explains the answer. 

What Is an Even or Odd Function Calculator?

An Even or Odd Function Calculator is a calculator available online that is used to check and identify the parity of the function f(x).

The parity of a function is one of the attributes that help in identifying the function.

Parity of a function refers to the attribute of the function being either odd or even. The parity of the function can be determined both algebraically and graphically. The even or odd function calculator determines the parity of the function in both.

To obtain the identification of the function, the even or odd function calculator offers the user an insert box to add to the function. Upon viewing the results, both algebraic as well as graphic results are provided by the calculator.

The even or odd function calculator provides the user with a detailed explanation of the identification of function f(x) by plugging in -x in the function and then comparing the result with the given function f(x).

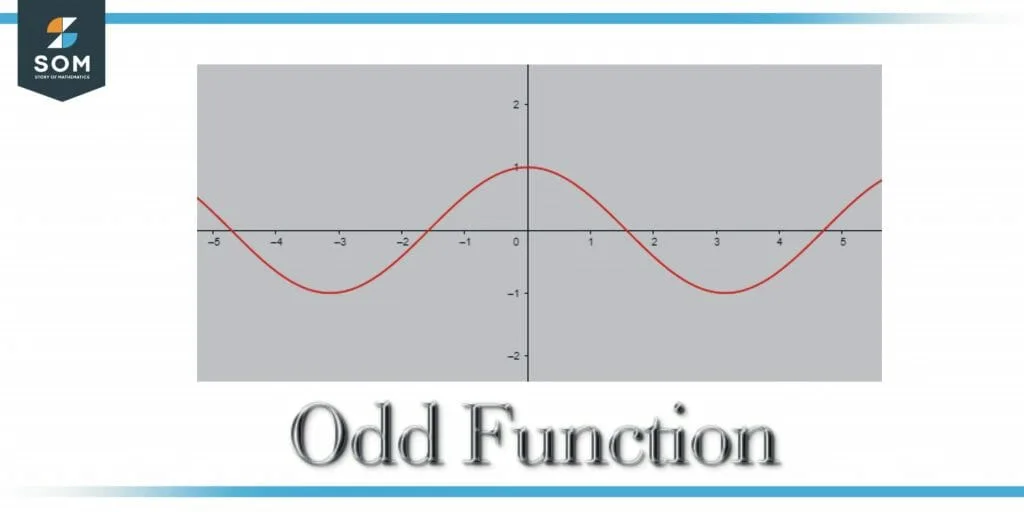
Figure 2 Odd Function

The even or odd function calculator also provides a graphical solution for function identification. The calculator does this by providing the graphical representation of the function f(x) and verifying its symmetry.

The calculator not only solves for functions being even or odd, but also provides identification solutions for functions that are neither even nor odd. 

How To Use the Even or Odd Function Calculator

The Even or Odd Function Calculator is fairly easy to use by following a few simple steps. It has an extremely user-friendly interface. The user of this calculator can easily navigate through the calculator options and obtain the desired results.

The interface of the even or odd function calculator consists of a prompt box that allows the user to enter the function. After entering the function, the user can then click on the next button to obtain the solution.

Given below is a step-by-step guide for using the even or odd function calculator and obtaining the identification solutions.

Step 1:

Choose any function for which you want to check the parity. There is no restriction in selecting the type of function. From algebraic functions to trigonometric functions, you can choose any for a parity check. 

Step 2:

Insert your function in the prompt box. The prompt box will have the statement “Is f(x) an even, odd (or neither) function.” You can plug in your function in place of f(x).

Step 3:

After entering your function, click on the box present next to the statement in the prompt box. This box is usually purple and is aligned with <> symbols. Simply click on it to obtain the solution.

Step 4:

Finally, after clicking the purple box, you will be able to view both the algebraic as well as graphic identification of function f(x). The algebraic identification will be given under ‘Parity Relation’ and the graphical one will be under “Plots.” 

This is how you will be able to obtain the identification or parity check of any function f(x).

How Does an Even or Odd Function Calculator Work?

The Even or Odd Function Calculator works by determining the parity of the function and displaying its graph. It is a reliable online calculator that provides quick and accurate parity checks for any type of function. As stated above, the calculator provides both algebraic as well as graphical identification.

To get into the details of the workings of this calculator, we have to know about odd and even functions.

Even Function

An even function is the one that provides the exact same function after inserting the value -x. This statement is more clear from the mathematical expression given below:

 f(x) = f(-x) 

In the graphical representation, an even function is always symmetric about the y-axis. If a function satisfies both these conditions, then the function is an even function.

Odd Function

An odd function is the one that provides the exact opposite function after plugging in the value -x in terms of signs. Mathematically, we can write it as:

f(-x) = -f(x) 

In the graphical representation, the functions which are always symmetric about the origin are identified as odd functions. 

Neither Even Nor Odd Function

If after putting the value -x, the function neither remains the same nor the opposite of the original function f(x), then such a function is recognized as neither even nor odd functions.

In graphical terms, these functions are neither symmetric about the y-axis nor symmetric about the origin. This is why these functions are called neither even nor odd functions. 

Let’s take a look at some solved examples for a better understanding. 

Solved Examples

Below are some solved examples that can help you in developing a better understanding of using the even or odd function calculator.

Example 1

Determine whether the following function is even, odd, or neither even nor odd:

\[ f(x) = -4x^{2} + 6 \]

Solution

For determining the parity check of this function, we need to analyze both the algebraic and the graphical solution. 

Simply insert the function f(x) in the prompt box of the calculator and press the button to obtain the solution. The calculator provides both algebraic and graphical solutions. 

For the algebraic solution, simply plug in -x in the function f(x). Plugging -x in the function f(x) gives us the following results:

\[ f(-x) = -4(-x)^{2} + 6 \]

\[ f(-x) = -4x^2 + 6 = f(x) \]

Since the algebraic result obtained is the same as the function, this indicates that the function is an even function.

f(-x) = f(x) for all values of x

Similarly, the following graphical result is obtained from the even or odd function calculator shown in Figure 3:

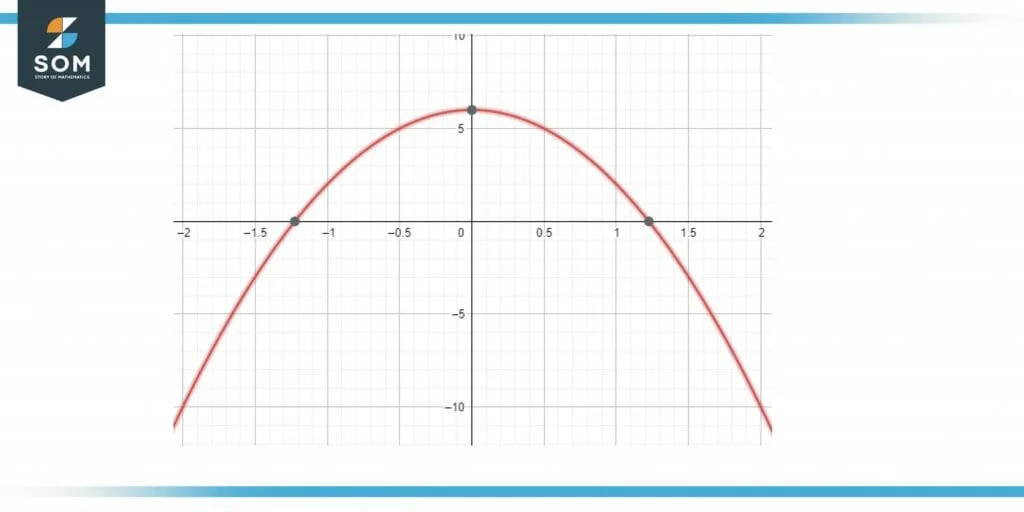
Figure 3 Example 1

The graphical solution shows that in all values and domains of x and -x, the function f(x) remains symmetric about the y-axis. If a function remains symmetric about the y-axis, then the function is an even function.

Hence, the given function f(x) is an even function as proven by both the algebraic and graphical solution.

Example 2

Determine whether the following function is even, odd, or neither even nor odd:

f(x) = sin(x) 

Solution

In the next example, the given function is a trigonometric function, which is:

 f(x) = sin(x) 

To determine the parity of the function, we will simply insert this trigonometric function f(x) in the prompt box of the calculator. Upon pressing the button, the calculator provides both algebraic and graphical results. 

The algebraic results provided by the calculator are given by inserting the value -x in the function f(x). 

 f(x) = sin(x) 

f(-x) = sin(-x) 

 f(-x) = -sin(x) = -f(x) 

Since the obtained answer is the complete opposite of the original function f(x), hence the given trigonometric function is odd. 

f(-x) = -f(x) for all values of x

The calculator also provides a graphical solution which is shown below in Figure 4:

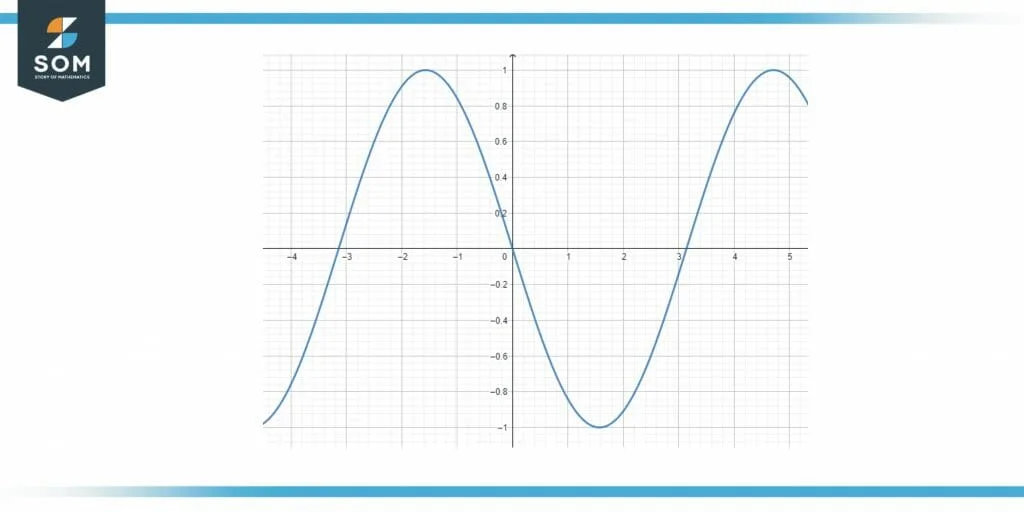
Figure 4 Example 2

Upon analyzing the graphical solution, the graph of the trigonometric function f(x) appears to be symmetric about the origin.

Such functions which are symmetric about the origin are odd.

Hence, the given function f(x) is an odd function as proved both by the algebraic and graphical solution.

Example 3

Determine whether the following function is even, odd, or neither even nor odd:

\[ f(x) = 2x^{2} + 2x \]

Solution

To determine the parity of the given function, simply insert this function f(x) in the prompt box and click on the button.

The even or odd function calculator will provide you with both algebraic as well as graphical solutions.

Upon analyzing the algebraic solution, simply plug in -x in the function f(x):

\[ f(-x) = 2(-x)^{2} + 2(-x) \]

\[ f(-x) = 2x^2 – 2x \]

From the result obtained, it is evident that this function f(-x) is neither the same as the original function f(x) nor the opposite of it, which indicates that the function f(x) is neither even nor odd.

Similarly, analyzing the following graphical solution provided by the calculator shown in Figure 5:

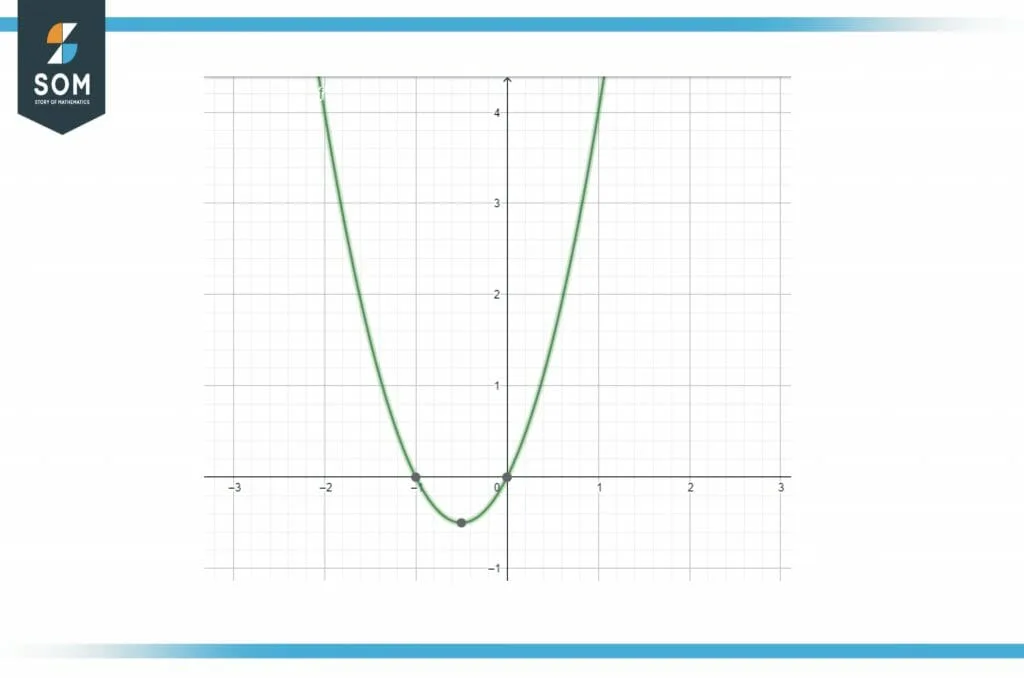
Figure 5 Example 3

The graph of the function f(x) is neither symmetric to the y-axis nor symmetric to the origin. This indicates that the given function f(x) is neither even nor odd. 

Hence, the function f(x) is neither even nor odd. 

Variable Isolation Calculator < Math Calculators List > Boolean Algebra Calculator

All, the images are created using GeoGebra.