
- What is the pressure difference?
- How much force is exerted on the roof? If the roof cannot withstand this much force, will it “blow in” or “blow out?”
The main objective of this problem is to determine the air pressure, pressure difference, and the force exerted by hurricane wind on the roof.
Bernoulli’s equation is being used to quantify the pressure difference. It is characterized as a statement of energy conservation for fluids in motion. This equation is considered as the fundamental behavior that reduces the pressure in high-velocity zones.
If the wind speed is $130 \, km/h$, the force on the roof will determine whether it will “blow in” or “blow out.”
Expert Answer
We will formulate the problem as follows:
Area of the roof $= A=6 \times 15 =90\, m^2$,
Velocity $= v = 130 \times \dfrac{1000}{3600} =36.11\, m/s$
(Velocity is converted from $km/h$ to $m/s$ )
It is well known that the air density is $\rho=1.2\,kg/m^3$
Since air pressure drops as air velocity increases, the air pressure above the roof is less than the air pressure inside the house.
1. Bernoulli’s equation can be used to quantify the difference in pressure:
$\Delta P=P_1-P_2=\rho \dfrac{v^2}{2}=1.2\times \dfrac{(36.11)^2}{2}=782.4\, Pa$
(where $Pa=kg/m\cdot s^2$)
2. Force on the roof is: $F=\Delta P\times A=782.4\times 90=70416\, N$
(Where $N=kg/m$ )
Hence, the roof will “blow out” due to excessive force.
Example
Water seeps at $2.1 m/s$ via a hosepipe at a pressure of $350000\, \,Pa$. There is no variation in height as when the pressure drops to atmospheric pressure $202100\,\, Pa$ at the nozzle. Evaluate the velocity of the water leaving the nozzle using Bernoulli’s equation. (Assume the density of water as $997\, kg/m^3$, and gravity $9.8\, m/s^2$.)
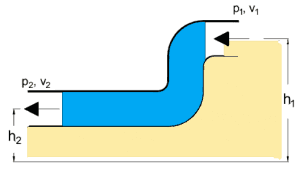
At one end of the hosepipe, we have
Pressure $=P_1=350000\,Pa$
Velocity $=v_1=2.1\,m/s$
At the exit of the nozzle,
Pressure $=P_2=202100\,Pa$
$\rho=997\,kg/m^3$ and $g=9.8\,m/s^2$ are constants.
Consider the Bernoulli’s equation:
$\dfrac{1}{2}\rho v^2_1+\rho { g h_1}+P_1=\dfrac{1}{2}\rho v^2_2+\rho {gh_2}+P_2$
Because there is no variation in height, therefore $h_1=h_2$ and we may deduct $\rho g h_1$ and $\rho g h_2$ from both sides, leaving us with:
$\dfrac{1}{2}\rho v^2_1+P_1=\dfrac{1}{2}\rho v^2_2+P_2$
To solve for $v_2$, restructure the problem algebraically and insert the integers.
$v_2^2=\dfrac{2}{\rho}\left(\dfrac{1}{2}\rho v^2_1+P_1-P_2\right) $
Numerical Results
Replace the given values in the equation above.
$v_2^2=\dfrac{2}{997}\left[\dfrac{1}{2}(997) (2.1)^2+(350000)-( 202100)\right]=301.1 $
$v_2=\sqrt{301.1}=17.4\,m/s$
Hence, the velocity of water leaving the nozzle is $17.4\,m/s$.
