• Home
  • >
  • Is -2 a Real Number? An Introduction To Real Numbers

Is -2 a Real Number? An Introduction To Real Numbers

Is 2 a real number titleIs -2 a real number? The answer is yes; $-2$ is a real number. Real numbers are the numbers that we use in our everyday lives. They are the numbers that we use when we count or measure things. They are the numbers that we use when we add, subtract, multiply, and divide.

The Real Number System

The real number system is a mathematical construct that allows us to represent and compare quantifiable data. It is the foundation on which all arithmetic and algebra are built. In mathematics, a real number is a value that represents a quantity along a continuum, such as $-2$ on a number line.

Real numbers can be positive or negative and include whole numbers, fractions, and decimals. They can also be rational or irrational. They comprise every number existing in the number line. Every number between $0$ to $1$, such as $0.5, 0.9999, 0.0001, 0.24374$, and all others, are all considered real numbers.

The real number system exists to distinguish between the set of real numbers and imaginary numbers. Note that imaginary numbers are the square root of a negative number and the solutions to the quadratic expression $x^2+a$, for some real number $a$. We denote the set of the real numbers as $\mathbb{R}$.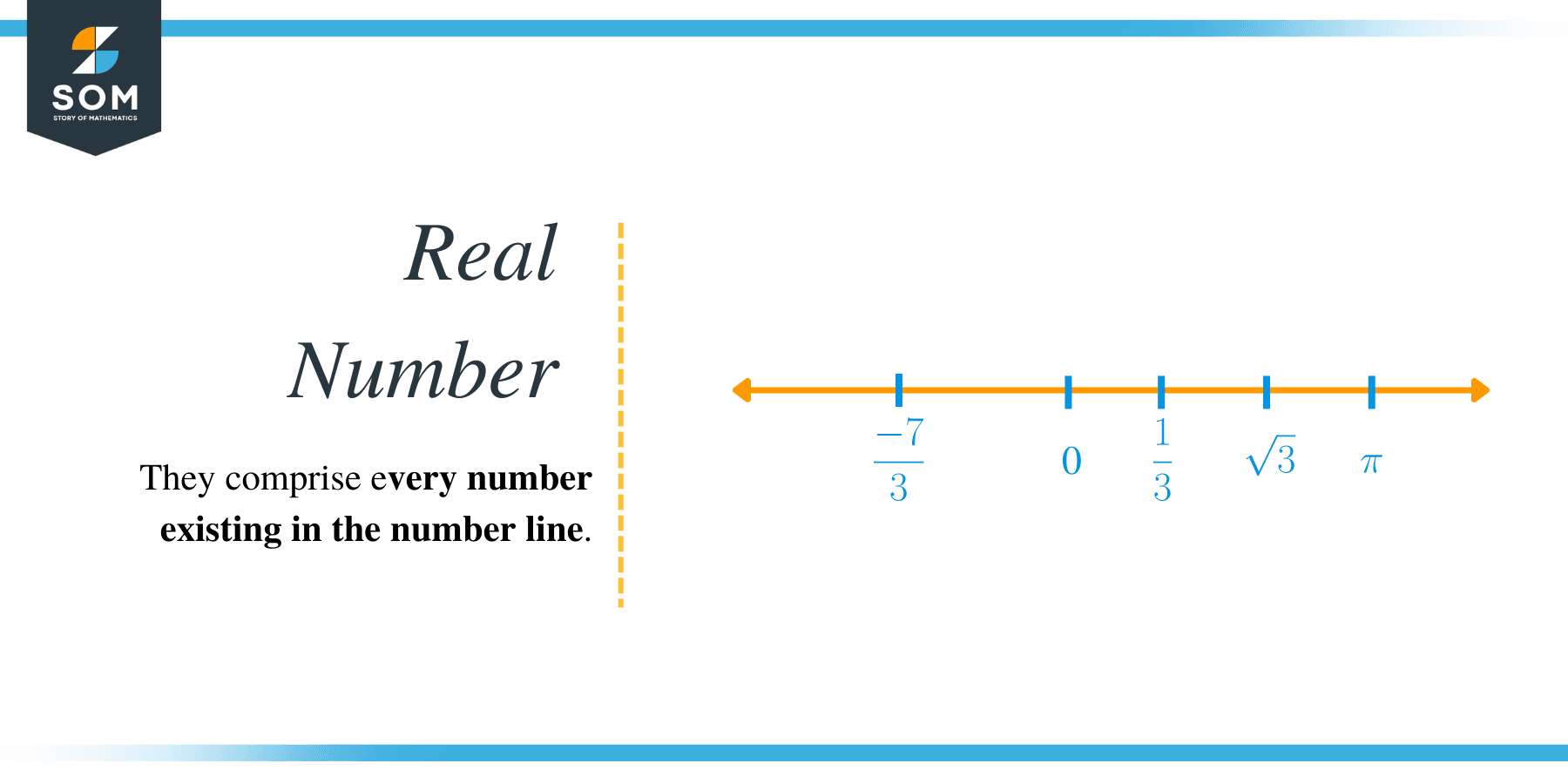Is 2 a real number what is real number

Example

Here are a few examples of real numbers.

  • $-1$ is a real number because it is a negative number.
  • The fraction $\dfrac{2}{3}$ is a real number.
  • $\sqrt{2}$ is a real number because it is a square root of a positive number.
  • $0.123123123123\dots$ is also a real number because it is a decimal.
  • The nonterminating number $\pi$ is also a real number.

 

On the other hand, the following expressions are not real numbers.

  • $\sqrt{-4}$ is not a real number because it is a square root of a negative number.
  • $\dfrac{2}{0}$ is not a real number because this fraction does not exist since you cannot divide a number by $0$.
  • $3i-1$ is not a real number because the expression has an imaginary unit $i$.

Is -2 a Real Number?

So, is $-2$ a real number? Yes! Indeed $-2$ is a real number. In fact, all negative numbers are real numbers.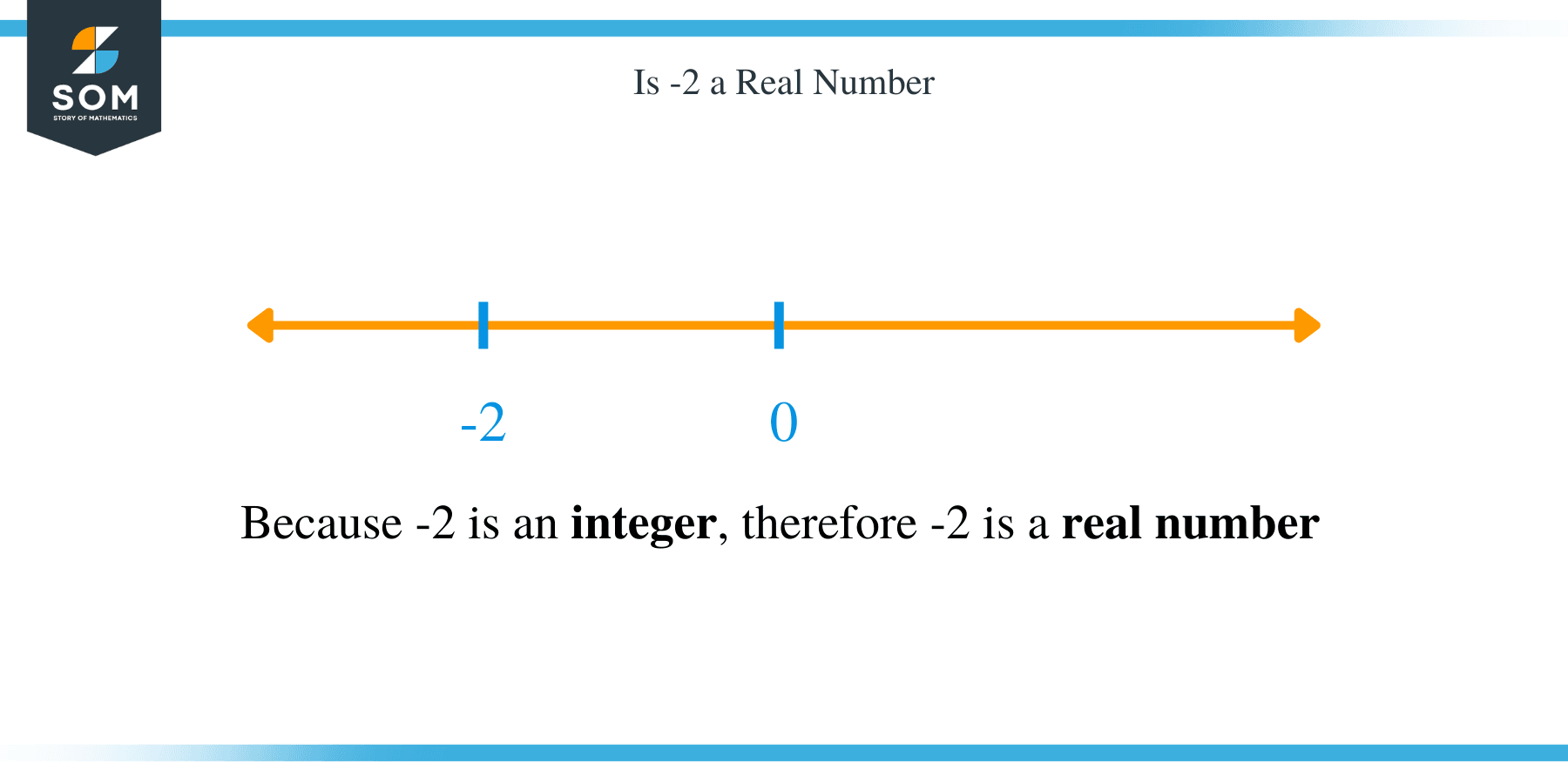Is 2 a real number answer

What Comprised the Real Number System?

The set of natural numbers, integers, and rational and irrational numbers make up the real number system. Every real number belongs to at least one of these sets of numbers. Some of the real numbers belong to more than one number system. For instance, $2$ is an integer, a natural number, and a rational number.

We look at each of these subsets of the real number systems and determine their elements and how they differ from each other.

The Natural Numbers

The natural numbers are the positive whole numbers $1, 2, 3, 4$, and so forth. In common language, the natural numbers are those that are used for counting and quantifying whole things. There is no largest natural number. The set of natural numbers is sometimes denoted by $\mathbb{N}$. \begin{align*} \mathbb{N}={1,2,3,4,5,\dots} \end{align*}

Example

  • $22$ is a natural number because it is a positive whole number.
  • $1,0000,0000$ is also a natural number.
  • The even numbers $2, 4, 6, 8, 10, \dots$ are all natural numbers.
  • $-2$ is not a natural number because it is not positive.
  • Zero is also not a natural number because it is also not positive.
  • The fraction $\dfrac{4}{5}$ is not a natural number because it is not a whole number.

The Integers

In mathematics, the integers are the subset of the real numbers that include all whole numbers and their opposites, the negative of all whole numbers. The set of integers is denoted by $\mathbb{Z}$. There is no smallest and largest integer because we cannot find the smallest negative integer and the largest positive integer. Integers are an important part of number theory and have numerous applications in other areas of mathematics, such as combinatorics, cryptography, and physics. \begin{align*} \mathbb{Z}=\{\dots,-3,-2,-1,0,1,2,3,\dots\} \end{align*}We can observe that the set of all natural numbers is smaller than the set of integers. This is because every natural number is an integer since a natural number is a positive whole number. Thus, the set of natural numbers is a subset of the set of integers.

Example

  • $-2$ is an integer because it is a negative whole number.
  • Zero is an integer that is neither positive nor negative. We say that zero is a nonpositive and nonnegative integer.
  • $100$ is an integer because it is a natural number.
  • The negative fraction $-\dfrac{4}{9}$ is not an integer because it is not a whole number.
  • $(-3)^2$ is an integer because the resulting number of that expression is $9$ which is a positive whole number.

Rational vs Irrational Numbers

A rational number is a real number that can be expressed as a fraction $\dfrac{p}{q}$, where $p$ and $q$ are integers, and $q$ is not equal to zero. On the other hand, irrational numbers are real numbers that are not rational numbers. This means that irrational numbers cannot be expressed as a ratio of two integers. Rational numbers are denoted by $\mathbb{Q}$, while irrational numbers are $\mathbb{Q}’$ in symbol since the set of irrational numbers is the complementary set of the set of rational numbers.

The set of rational numbers is composed of whole numbers, integers, fractions, terminating decimals, and repeating nonterminating decimals because these numbers have equivalent fractions. Whereas irrational numbers are numbers that include square roots, cube roots, and numbers that are infinitely nonrepeating decimal expansions.
\begin{align*}
\mathbb{Q}=\{\dfrac{p}{q}\, ∶\,p,q\in\mathbb{Z}\}
\end{align*}
and
\begin{align*}
\mathbb{Q}’=\mathbb{R}-\mathbb{Q}
\end{align*}

We also know that any integer can be expressed as a ratio of two integers. Therefore, the set of integers is a subset of the set of rational numbers. This means that every natural number and integer is a rational number and can never be irrational.

Example

The following are some examples of rational numbers.

  • $\dfrac{5}{7}$ is a rational number because it is a ratio of two integers $5$ and $7$.
  • Zero is a rational number because zero can always be expressed as $\dfrac{0}{a}$, where $a$ is an integer. Thus, zero is always a ratio of two integers.
  • Note that $-2=\dfrac{4}{-2}=\dfrac{-10}{5}$. This means that we can always write $-2$ in a fraction form that, when reduced or expressed in the simpler form, will give us $-2$. Hence, $-2$ is a rational number.
  • The repeating decimal $0.123123123\dots$ is a rational number because this decimal is equivalent to the fraction $\dfrac{41}{333}$.

Here are some examples of irrational numbers.

  • $\sqrt{2}$ is irrational because it cannot be expressed as a ratio of two integers.
  • The ratio of a circle’s circumference to its diameter, which is equal to the real number $\pi$ is an irrational number. Note that $\pi$ is a nonterminating decimal approximately equal to $3.14159\dots$ and thus, cannot be expressed as a fraction.
  • The Euler’s constant $e$ is also an irrational number.
    The number $-\dfrac{\pi}{3}$ is also irrational because it is a ratio of $-\pi$ and $3$, and $-\pi$ is not an integer.

Relationship Between Each Number Systems

Now that we already know the different number systems that constitute the real number system, we look at their relationships and determine which number system is contained with the other. Their relationship can be summarized in the following statements.

  • All natural numbers, integers, rational numbers, and irrational numbers are real numbers.
  • Every natural number is an integer.
  • Every integer is a rational number.
  • Every real number that is not a rational number is an irrational number.
  • The set of real numbers is a union of the sets of rational numbers and irrational numbers.
    \begin{align*}
    \mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\\
    \mathbb{R}=\mathbb{Q}\cup\mathbb{Q}’
    \end{align*}

Example

  • $-2$ is a real number because it is a natural number, an integer, and a rational number.
  • Zero is an integer and a rational number but not a natural number.
  • The fraction $\dfrac{3}{4}$ is a rational number but neither an integer nor a natural number.
  • $2\sqrt{2}$ is an irrational number, so it is not a rational number, an integer, and a natural number.
  • The imaginary number $2i$ is not a real number, and thus, it is neither rational, irrational, an integer, nor a natural number.

Frequently Asked Questions About Real Numbers

We gather some of the frequently asked questions regarding real numbers to give direct-to-point answers for you.

Is 0 a Real Number?

Yes. Zero is a real number because it is an integer and a rational number.

Is Negative 8 a Real Number?

Yes. Negative $8$ is a real number because it is an integer.

What Is Not a Real Number?

All numbers that have an imaginary part or those numbers that are expressed with an imaginary unit $i$ are not real numbers. The square root of a negative real number is also not a real number.

Is Negative a Real Number?

A negative number is a real number. Negative rational numbers and negative irrational numbers are all irrational numbers.

Is 1/2 a Real Number?

Yes, $\dfrac{1}{2}$ is a real number. The fraction $\dfrac{1}{2}$ is a rational number, and thus, it follows that it is a real number.

Conclusion

The real numbers, which include all the rational and irrational numbers, are the foundation of the number system. Here are the most important points in our discussion.

  • $-2$ is a real number because it is an integer and a rational number.
  • The real number system is comprised of all rational numbers and all irrational numbers.
  • A natural number is a positive whole number.
  • The set of integers is composed of the natural numbers, the negative of the natural numbers, and zero.
  • Rational numbers are numbers that can be expressed as a ratio of two integers, while a number that is not rational is irrational.

The real number system is important in mathematical and scientific applications but is also used in everyday life, for example, in the measurement of time, length, and temperature. Thus, being able to distinguish whether $-2$ is a real number or not is important because real numbers are a critical part of mathematics used to solve a variety of problems.