Intercepted Arc – Explanation & Examples

Now that we have learned all the basic parts of the circle let’s go into something complex. We are talking about the intercepted arc, which is formed in the circle due to external lines. If you are really good at angles, then this lesson should not be a problem for you to understand.

We saw all the basic definitions of parts of circles before, like diameter, chord, vertex, and central angle; if you have not, please go through the previous lessons because these parts have a use in this lesson.

In this article, you will learn:

• The definition of an intercepted arc,
• how to find an intercepted arc and,
• intercepted arc formula.

What is an Intercepted Arc?

To recall, an arc is part of the circumference of a circle. An intercepted arc can therefore be defined as an arc formed when one or two different chords or line segments cut across a circle and meet at a common point called a vertex.

It is important to note that the lines or the chords can either meet in the middle of a circle, on the other side of a circle or outside a circle.

Or we can also define the intercepted arc as when two lines cross a circle at two different points, the part of the circle between the points of intersection forms the intercepted arc.

How to Find Intercepted Arc?

There exist some interesting relationships between an intercepted arc and the inscribed and central angle of a circle. In geometry, an inscribed angle is formed between the chords or lines cutting across a circle.

The central angle is an angle formed by two radii that joins the ends of a chord to the center of a circle. These relationships between different intercepted arcs and their corresponding inscribed angles form the intercepted arc formula.

Let’s take a look.

Intercepted arc formula

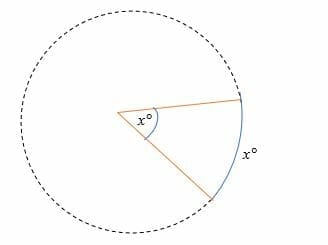
• Intercepted arc formula for lines meeting in the middle of a circle

The central angle = the measure of the intercepted arc

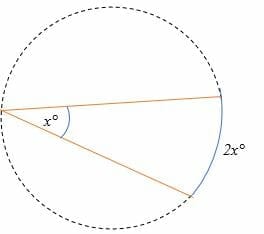
• Intercepted arc formula for chords meeting on the other side of a circle.

The inscribed angle = 1/2 × intercepted arc

Or

2 x the inscribed angle = the intercepted arc

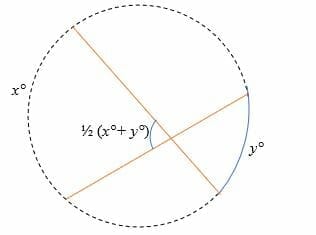
Intersecting chords:

For intersecting chords, the intercepted arc is given by,

The inscribed angle = half the sum of intercepted arcs.

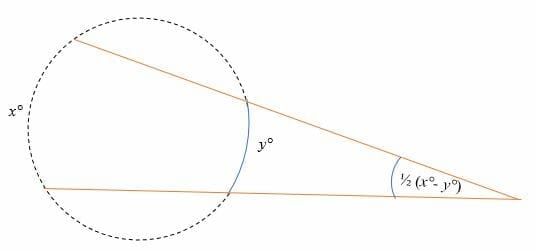
External inscribed angle:

The size of the vertex angle outside the circle = 1/2 × (difference of intercepted arcs)

Worked out examples about the intercepted arc.

Example 1

Find angle ABC in the circle shown below.

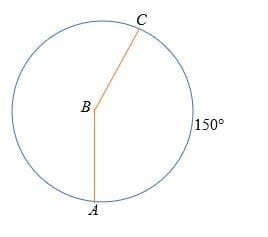
Solution

Given, the intercepted arc = 150°

The central angle = intercepted arc

Therefore, ∠ABC = 150°

Example 2

Determine the value of x in the circle shown below.

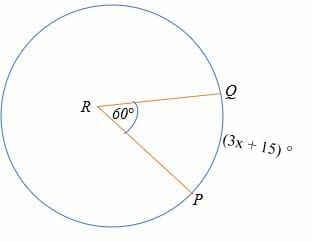
Solution

The central angle = intercepted arc

60° = (3x + 15) °

Simplify

60° = 3x + 15°

Subtract 15° on both sides.

45° = 3x

Divide both sides by 3

x = 15°

So, the value of x is 15°.

Example 3

Find the value of the intercepted arc in the diagram shown below.

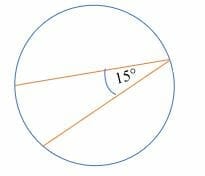
Solution

Given,

The inscribed angle = 15°

By the formula,

The inscribed angle = ½ × intercepted arc

15° = ½ x intercepted arc

Therefore, the measure of the intercepted arc is 30°.

Example 4

If the intercepted arc in the diagram below is 160°, determine the value of x.

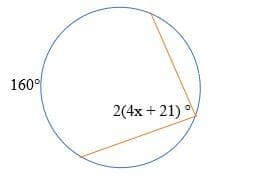
Solution

Given,

The intercepted arc =160°

The inscribed angle = ½ × intercepted arc

The inscribed angle = ½ x 160°

= 80°

So, we have,

2(4x + 21) ° = 80°

8x + 42° = 80°

Subtract 42° on both sides.

8x = 38°

Divide both sides by 8 to get.

x = 4.75°

Thus, the value of x is 4.75°

Example 5

Find the value of the inscribed angle in the following diagram.

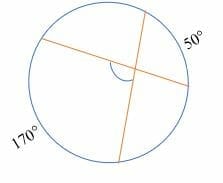
Solution

The inscribed angle = half the sum of intercepted arcs.

= ½ x (170° + 50°)

= ½ x 220°

= 110°

So, the inscribed angle is 110°.

Example 6

Find the value of x in the diagram shown below.

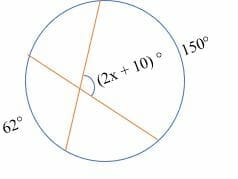
Solution

Given the intercepted arcs as 62° and 150°

The inscribed angle = half the sum of intercepted arcs.

The inscribed angle = ½ (62° + 150°)

= ½ x 212°

= 106°

Now solve for x.

(2x + 10) ° = 106°

Simplify.

2x + 10° =106°

Subtract 10° on both sides.

2x = 96

On dividing both sides by 2, we get,

x = 48°

Hence, the value of x is 48 degrees.

Example 7

Find the external vertex angle in the diagram shown below.

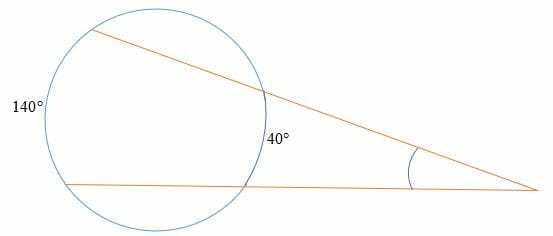
Solution

Now you need to recall the properties we studied above.

The size of the vertex angle outside the circle = 1/2 × (difference of intercepted arcs)

Vertex angle = ½ (140° – 40°)

= ½ x 100°

= 50°

So, the measure of angle with vertex outside the circle is 50°.