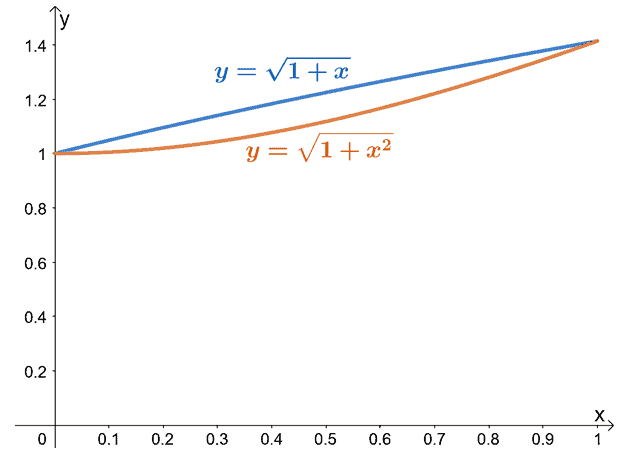Integral Properties – Definition, Process, and Proof
Learning about the
integral properties is essential if we want to evaluate integrals faster. These properties come in handy when we need to strategically manipulate expressions when proving inequalities and confirming equations.
Mastering the integral properties will help when working with complex integrals. Learning how to prove them also shows how closely related derivatives and integrals are with each other.In this article, we’ll study the common properties of indefinite and definite integrals. Our discussion will use concepts we’ve learned from our previous discussions, so review the following topics or make sure that you have a strong grip on the following topics:
- Recall how we’ve defined definite integrals from our discussion on the theorem of fundamental calculus.
- When proving these properties, we’ll be using some fundamental derivative rules, so take a quick look at this article in case you need a quick refresher.
- Refresh your knowledge of antiderivatives here as well.
We’ll begin by understanding the three fundamental properties of indefinite integrals. We can then move on to exploring more complex properties for definite integrals. Our discussion is going to be thorough, so take your time absorbing each section before moving on to the next. Are you ready? Let’s go ahead and dive in!
What are the properties of integrals?
The properties of integrals
help us in evaluating indefinite and definite integrals of
functions that contain multiple terms. These properties will also help
break down definite integrals so that we can
evaluate them more efficiently.Recall that when we differentiate complex functions, we use properties to simplify our process (ie $\dfrac{d}{dx} k\cdot f(x) = k \dfrac{d}{dx} f(x)$). We use similar properties to simplify process of evaluating indefinite and definite integrals.Let’s say we have the following real numbers: $a$, $b$, $k$, $A$, and $B$. Given that $f(x)$ and $g(x)$ are integrable over the interval, $[a, b]$, the functions will satisfy the following properties for indefinite integrals:
| Properties of Indefinite Integrals |
| Constant Multiple Property | $\int k \cdot f(x) \phantom{x}dx = k \int f(x) \phantom{x}dx $ |
| Sum Property | $\int [f(x) + g(x)]\phantom{x}dx = \int f(x) \phantom{x}dx + \int g(x) \phantom{x}dx $ |
| Difference Property | $\int [f(x) – g(x)]\phantom{x}dx = \int f(x) \phantom{x}dx – \int g(x) \phantom{x}dx $ |
The sum and difference properties extend to definite integrals as well. Below are essential properties that we’ll need when simplifying expressions with definite integrals.
| Properties of Definite Integrals |
| Sum or Difference | $\int_{a}^{b} [f(x) \pm g(x)]\phantom{x}dx = \int_{a}^{b} f(x) \phantom{x}dx \pm \int_{a}^{b} g(x) \phantom{x}dx $ |
| Constant Multiple | $\int_{a}^{b} [k\cdot f(x)]\phantom{x}dx = k\int_{a}^{b} f(x) \phantom{x}dx$ |
| Reverse Interval | $\int_{a}^{b} f(x)\phantom{x}dx = -\int_{b}^{a} f(x) \phantom{x}dx$ |
| Zero-length Interval | $\int_{a}^{a} f(x)\phantom{x}dx = 0$ |
| Combining Intervals | $\int_{a}^{b} f(x)\phantom{x}dx + \int_{b}^{c} f(x)\phantom{x}dx = \int_{a}^{c} f(x)\phantom{x}dx$ |
| Comparison Property | i) When $f(x) \geq 0$ for $x \in [a, b]$, $\int_{a}^{b} f(x)\phantom{x}dx \geq 0$.ii) When $f(x) \geq g(x)$ for $x \in [a, b]$, $\int_{a}^{b} f(x)\phantom{x}dx \geq \int_{a}^{b} f(x)\phantom{x}dx $.iii) When $m \leq f(x) \leq M$ and $x\in [a, b]$, $m(b – a) \leq \int_{a}^{b} f(x)\phantom{x} dx \leq M(b –a)$. |
We’ll show you how to apply these indefinite and definite integral properties. We’ll also show you how some of these properties were derived. Before we move to the next part of our discussion, review all nine properties once again. When you’re ready, let’s move on to understanding how these properties were derived.
How to apply the different integral properties?
The best way to understand and master these integral properties is by learning the conditions required by these properties and knowing the best time to apply them. We’ll break down the steps for each property and show you examples of how each of these properties is applied.
Understanding the constant multiple property of integrals
The constant multiple property applies to both indefinite and definite integrals. This means that when we’re evaluating
the integral of a function, $\boldsymbol{f(x)}$,
and a constant factor, $\boldsymbol{c}$, the resulting expression is simply
equal to the product of the constant and the integral of $\boldsymbol{f(x)}$.\begin{aligned} \int {\color{Teal} k}\cdot {{\color{DarkOrange} f(x)}}\phantom{x}dx &= {\color{Teal}k}\int {{\color{DarkOrange} f(x)}}\phantom{x}dx\\ \int_{a}^{b} {\color{Teal} k}\cdot {{\color{DarkOrange} f(x)}}\phantom{x}dx &= {\color{Teal}k}\int_{a}^{b} {{\color{DarkOrange} f(x)}}\phantom{x}dx\end{aligned}Let’s go ahead and apply this property to simplify the integral shown below. Make sure to review your knowledge of antiderivative formulas
here or bring out your notes since we’ll be applying them to simplify the expression.This means that if we have $\int -3x^2 \phantom{x}dx$, we can factor out $-3$ then simply evaluate $\int x^2\phantom{x}dx$ using the power rule, $\int x^n \phantom{x}dx = \dfrac{x^{n + 1}}{n +1} + C$.\begin{aligned} \int {\color{Teal} -3}\cdot {{\color{DarkOrange} x^2}}\phantom{x}dx &= {\color{Teal}-3}\int {{\color{DarkOrange} x^2}}\phantom{x}dx\\&= -3 \left(\dfrac{x^{2 + 1}}{2 + 1}\right ) + C\\&=-3 \cdot \dfrac{x^3}{3} + C\\&= -x^3 + C\end{aligned}We can also apply a similar process when evaluating definite integrals. Just keep in mind that according to the
fundamental theorem of calculus, we have $\int_{a}^{b} f(x)\phantom{x}dx = F(b) – F(a)$, where $F(x)$ is the antiderivative of $f(x)$.
Understanding the sum and difference properties of integrals
These two properties tell us that
if a function can be broken down as a sum or difference of simpler functions, we can find the function’s integral by
adding or subtracting the integrals of the simpler functions.\begin{aligned} \int [{\color{Teal} f(x)} \pm {{\color{DarkOrange} g(x)}}]\phantom{x}dx &= \int {\color{Teal}f(x)} \phantom{x}dx\pm \int {{\color{DarkOrange} g(x)}}\phantom{x}dx\\\int_{a}^{b} [{\color{Teal} f(x)} \pm {{\color{DarkOrange} g(x)}}]\phantom{x}dx &= \int_{a}^{b} {\color{Teal}f(x)}\phantom{x}dx \pm \int_{a}^{b} {{\color{DarkOrange} g(x)}}\phantom{x}dx\end{aligned}We’ll show you two examples: one is an application of the sum property on an indefinite integral and the second is an application of the difference on a definite integral.
| Indefinite Integral | \begin{aligned} \int 2x^2 + x&= \int ({\color{Teal} 2x^2} + {{\color{DarkOrange} x}})\phantom{x}dx\\ &= \int {\color{Teal}2x^2}\phantom{x}dx + \int {{\color{DarkOrange} x}}\phantom{x}dx\\&= {\color{Teal}2}\int x^2\phantom{x}dx + \int x \phantom{x}dx,\phantom{x}{\color{Teal}\text{Constant Multiple Property}}\\&= 2{\color{Teal}\left(\dfrac{x^{2 + 1}}{2 + 1} \right )} + {\color{Teal}\dfrac{x^{1 + 1}}{1 + 1} }+ C,\phantom{x}\color{Teal}\text{Power Rule}\\&= \dfrac{2x^3}{3} + \dfrac{x^2}{2} + C\end{aligned} |
| Definite Integral | \begin{aligned} \int_{0}^{4} 3x^2 – 6x&= \int_{0}^{4} ({\color{Teal} 3x^2} – {{\color{DarkOrange} 6x}})\phantom{x}dx\\ &= \int_{0}^{4} {\color{Teal}3x^2}\phantom{x}dx – \int_{0}^{4} {{\color{DarkOrange} 6x}}\phantom{x}dx\\&= {\color{Teal}3}\int x^2\phantom{x}dx – {\color{Teal}6}\int x \phantom{x}dx,\phantom{x}{\color{Teal}\text{Constant Multiple Property}}\\&= 3{\color{Teal}\left(\dfrac{x^{2 + 1}}{2 + 1} \right )} – 6\left({\color{Teal}\dfrac{x^{1 + 1}}{1 + 1} }\right )+ C,\phantom{x}\color{Teal}\text{Power Rule}\\&= \dfrac{3x^3}{3} – \dfrac{6x^2}{2} + C\\&=x^3 – 3x^2 + C\end{aligned} |
This property is quite similar to the addition and subtraction rules for differentiation and this makes since integration and differentiation are closely related to each other. Use a similar process to prove the different properties of definite and indefinite integrals.
Understanding the properties helpful in manipulating definite integrals
Let’s now understand how to apply the three properties: reversal interval, combining interval, and zero-length interval properties. The three properties focus on
how the upper and lower limits affect a definite integral’s value.
- Using the reverse interval property, we can rewrite the definite integral of a function as the negative definite integral of the same function when we reverse the positions of its lower and upper limits.
\begin{aligned}\int_{a}^{b} f(x)\phantom{x}dx = -\int_{b}^{a} f(x) \phantom{x}dx\end{aligned}
- When the lower and upper limits of a function’s definite integral are equal, its value is equal to zero. We call this the zero-length interval property.
\begin{aligned}\int_{a}^{a} f(x)\phantom{x}dx = 0\end{aligned}
- Through the combining interval property, we can combine two or more definite integrals sharing the same function. This can be possible the two definite integrals being combined have identical upper and lower limits.
\begin{aligned}\int_{a}^{b} f(x)\phantom{x}dx + \int_{b}^{c} f(x)\phantom{x}dx = \int_{a}^{c} f(x)\phantom{x}dx\end{aligned}Here are examples of definite integrals where we can use each of these properties to simplify the expressions shown below.
| Reverse Interval | \begin{aligned} \int_{0}^{4} 4x \phantom{x}dx&= -\int_{4}^{0} 4x\phantom{x}dx \\\int_{-2}^{2} (5x^2 -1) \phantom{x}dx&= -\int_{2}^{-2} (5x^2 -1) \phantom{x}dx\\\int_{-1}^{4} \dfrac{x^2 -1}{x + 3} \phantom{x}dx&= -\int_{4}^{-1} \dfrac{x^2 -1}{x + 3} \phantom{x}dx\end{aligned} |
| Zero-Length Interval | \begin{aligned}\int_{4}^{4} (4x – 3)\phantom{x}dx &= 0\\\int_{2}^{2} \sqrt{x^2 – 4x + 4}\phantom{x}dx &= 0\\\int_{-3}^{-3}\dfrac{1}{x^2 +1}\phantom{x} dx &= 0\end{aligned} |
| Combining Interval | \begin{aligned}\int_{-2}^{0} (2x + 5)\phantom{x}dx + \int_{0}^{2} (2x + 5)\phantom{x}dx&= \int_{-2}^{2} (2x + 5)\phantom{x}dx\\\int_{-4}^{2} \sqrt{x+ 4}\phantom{x}dx + \int_{2}^{4} \sqrt{x+ 4} \phantom{x}dx&= \int_{-4}^{4} \sqrt{x+ 4} \phantom{x}dx\\ \int_{2}^{5} \dfrac{x}{x^2 + 4} \phantom{x}dx + \int_{5}^{10} \dfrac{x}{x^2 + 4} \phantom{x}dx&= \int_{2}^{10} \dfrac{x}{x^2 + 4} \phantom{x}dx \end{aligned} |
There are instances when we need to manipulate intervals and positions on the integrals’ lower and upper limits in order for us to evaluate definite integrals. Knowing these three properties by heart will also fasten the time it takes us to evaluate complex definite integrals.
Understanding the comparison property of integrals
We’ll now work on properties that involve comparing the definite integrals using inequalities.
- When the function is above or along the $\boldsymbol{x}$-axis throughout the interval, $[a, b]$, then the definite integral of $\boldsymbol{f(x)}$ throughout this interval will always be positive.
\begin{aligned}f(x) &\geq 0\\ \Rightarrow \int_{a}^{b} f(x) \phantom{x}dx &\geq 0\end{aligned}
- If the function, $\boldsymbol{f(x)}$, is lying below the function, $\boldsymbol{g(x)}$, within the interval of $[a, b]$, the $\boldsymbol{f(x)}$‘s definite integral will be less than that of $\boldsymbol{g(x)}$‘s definite integrals when they share the same lower and upper limits: $x =a$ and $x =b$, respectively.
\begin{aligned}f(x) &\leq g(x)\\ \Rightarrow \int_{a}^{b} f(x) \phantom{x}dx &\leq \int_{a}^{b} g(x) \phantom{x}dx \end{aligned}
- Use the fact that $\boldsymbol{m}$ and $\boldsymbol{M}$ are the minimum and maximum values possible for $\boldsymbol{f(x)}$ throughout the interval, $[a, b]$. The definite integral of $\boldsymbol{f(x)}$ throughout the interval will have a minimum and maximum values of $\boldsymbol{m(b –a)}$ and $\boldsymbol{M(b –a)}$, respectively.
\begin{aligned} m\leq f(x) &\leq M\\ \Rightarrow m(b -a) \leq \int_{a}^{b} f(x) \phantom{x}dx &\leq M(b – a)\end{aligned}For example, we can use the second inequality to prove that $\int_{0}^{1} \sqrt{1 + x^2} \phantom{x}dx \leq \int_{0}^{1} \sqrt{1 + x}\phantom{x}dx$.
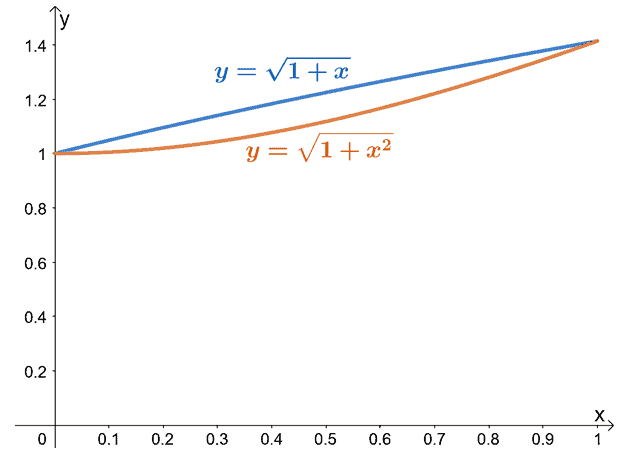
How to prove the integral properties?
Now that we’ve learned about the properties that can help us in simplifying indefinite and definite integrals, it’s time that we learn how some of these properties were derived. In this section, we’ll show you the proof for the addition, constant multiple, and reverse interval properties of integrals.\begin{aligned}\int k \cdot f(x) \phantom{x}dx &= k \int f(x) \phantom{x}dx\\\int [f(x) + g(x)]\phantom{x}dx &= \int f(x) \phantom{x}dx + \int g(x) \phantom{x}dx \\\int_{a}^{b} f(x)\phantom{x}dx &= -\int_{b}^{a} f(x) \phantom{x}dx\end{aligned}We’ll need some of the properties and
derivative rules we’ve learned from our differential calculus classes, so make sure to refresh your knowledge. In addition, recall that differentiation’s process is the inverse of integration.\begin{aligned}\dfrac{d}{dx} \int f(x) \phantom{x}dx &= f(x)\\\int f^{\prime}(x) \phantom{x}dx &= f(x) + C\end{aligned}Keep this relationship in mind when deriving the rest of the formulas discussed in the previous section. For now, let’s begin by deriving the constant multiple property of integrals.
Proving the constant multiple property of integrals
To prove this property, we’ll need to use the constant multiple property of derivatives, $\dfrac{d}{dx} k \cdot f(x) = k \dfrac{d}{dx} f(x)$. What we’ll do here is take the derivative of $\int k \cdot f(x) \phantom{x}dx$ and $k\int \cdot f(x) \phantom{x}dx$ with respect to $x$.\begin{aligned} \dfrac{d}{dx}\left[\int k \cdot f(x) \phantom{x}dx \right] &= k\cdot f(x)\\\dfrac{d}{dx} \left[k\cdot\int f(x)\phantom{x}dx \right ] &= k\cdot\dfrac{d}{dx}\int f(x)\phantom{x}dx\\&= k\cdot f(x)\\\\\dfrac{d}{dx}\left[\int k \cdot f(x) \phantom{x}dx \right]&= \dfrac{d}{dx} \left[k\cdot\int f(x)\phantom{x}dx \right ]\end{aligned}For the two sides of the equation to be true, $\int k\cdot f(x)\phantom{x}dx $ must be equal to , $k \int f(x)\phantom{x}dx $. Hence, confirming the constant multiple property of integrals.
Proving the sum property of integralsWe’ll apply a similar process to prove the sum property of integrals using the sum rule for derivatives, $\dfrac{d}{dx} [f(x) + g(x)] = \dfrac{d}{dx} f(x) + \dfrac{d}{dx} g(x)$. Take the derivative of $\int [f(x) + g(x)]\phantom{x} dx$ and $\int f(x)\phantom{x} dx + \int f(x)\phantom{x} dx $.\begin{aligned} \dfrac{d}{dx}\int [f(x) + g(x)] \phantom{x}dx &= f(x) + g(x)\\\dfrac{d}{dx} \left[\int f(x)\phantom{x}dx +\int g(x)\phantom{x}dx\right ] &= \dfrac{d}{dx}\int f(x)\phantom{x}dx + \dfrac{d}{dx}\int g(x)\phantom{x}dx\\&= f(x) + g(x)\\\\\dfrac{d}{dx}\int [f(x) + g(x)] \phantom{x}dx &= \dfrac{d}{dx} \left[\int f(x)\phantom{x}dx +\int g(x)\phantom{x}dx\right ]\end{aligned}Since both sides of the equation are equal, the integral expressions will also be equal.\begin{aligned} \int [f(x) + g(x)] \phantom{x}dx &= \int f(x)\phantom{x}dx +\int g(x)\phantom{x}dx\end{aligned}This confirms the sum property of indefinite integrals. We can apply a similar process to confirm the sum property of definite integrals, $\int_{a}^{b} [f(x) + g(x)] \phantom{x}dx = \int_{a}^{b} f(x)\phantom{x}dx +\int g(x)\phantom{x}dx$.
Proving the reverse length property of integrals
For this property, let’s recall the second part of the fundament theorem of calculus: $\int_{a}^{b} f(x)\phantom{x}dx = F(b) – F(a)$, where $F(x)$ is the antiderivative of $f(x)$. We can use this theorem to rewrite $-\int_{b}^{a}f(x) \phantom{x}dx$.\begin{aligned} -\int_{b}^{a} f(x)\phantom{x}dx &= -[F(a) – F(b)]\\&= -F(a) + F(b)\\&= F(b) – F(a)\\&= \int_{a}^{b} f(x)\phantom{x}dx\end{aligned}Hence, we’ve shown that reversing the limits’ positions will simply change the resulting value of the definite integral.We can use similar processes when proving the rest of the properties. But we left that for you to work on your own and some, we have included in the exercises shown below!Make sure to keep your notes handy though when working on the rest of the problems.
Example 1Use the fact that $\int_{0}^{6} f(x) \phantom{x} dx = 12$ and $\int_{-6}^{0} f(x) \phantom{x} dx = 20$ to determine the value of $\int_{-6}^{6} f(x) \phantom{x} dx$.
SolutionWe begin by recalling the definite integral property, $\int_{a}^{b} f(x)\phantom{x} dx + \int_{b}^{c} f(x)\phantom{x} dx = \int_{a}^{c} f(x) \phantom{x}dx$. We can use this property to combine the two given definite integrals.\begin{aligned} \int_{0}^{6} f(x) \phantom{x} dx + \int_{-6}^{0} f(x) \phantom{x} dx &= \int_{-6}^{0} f(x) \phantom{x} dx + \int_{0}^{6} f(x) \phantom{x} dx\\&= \int_{-6}^{6} f(x) \phantom{x} dx\end{aligned}We’ve shown that we can find the value of $\int_{-6}^{6} f(x)\phantom{x} dx$ by adding the values of the definite integrals, $\int_{0}^{6} f(x) \phantom{x} dx = 12$ and $\int_{-6}^{0} f(x) \phantom{x} dx = 20$.\begin{aligned} \int_{-6}^{6} f(x) \phantom{x} dx &= 12 + 20\\&= 32\end{aligned}Hence, we have $\int_{-6}^{6} f(x) \phantom{x} dx = 32$.
Example 2Use the fact that $\int_{0}^{3} f(x) \phantom{x} dx = 18$ and $\int_{0}^{10} f(x) \phantom{x} dx =40$ to determine the value of $\int_{3}^{10} f(x) \phantom{x} dx$.
SolutionWe’ll also be using the same property, $\int_{a}^{b} f(x)\phantom{x} dx + \ int_{b}^{c} f(x)\phantom{x} dx = \int_{a}^{c} f(x) \phantom{x}dx$, to answer this problem.Rewrite the expression so that we can expression $\int_{3}^{10} f(x) \phantom{x} dx$ in terms of $\int_{0}^{3} f(x) \phantom{x} dx$ and $\int_{0}^{10} f(x) \phantom{x} dx$.\begin{aligned}\int_{0}^{10} f(x) \phantom{x} dx &= \int_{0}^{3} f(x) \phantom{x} dx + \int_{3}^{10} f(x) \phantom{x} dx \end{aligned}Substitute the values of the two definite integrals then isolate $\int_{3}^{10} f(x) \phantom{x} dx$ on one side of the equation.\begin{aligned}40 &= 18 + \int_{3}^{10} f(x) \phantom{x} dx\\40 – 18 &= \int_{3}^{10} f(x) \phantom{x} dx\\\int_{3}^{10} f(x) \phantom{x} dx &= 22 \end{aligned}This means that by combining intervals, we were able to determine the value of $\int_{3}^{10} f(x) \phantom{x} d$. In fact, it’s equal to $22$.
Example 3Prove the definite integral property, $\int_{a}^{b} f(x) \phantom{x}dx + \int_{b}^{c} f(x) \phantom{x}dx = \int_{a}^{c} f(x) \phantom{x}dx $.
SolutionRecall that when $F(x)$ is the antiderivative of $f(x)$, we have $\int_{a}^{b} f(x)\phantom{x} dx = F(b) – F(a)$. Use the second part of the fundamental theorem of calculus to rewrite the right-hand side of the equation.\begin{aligned}\int_{a}^{b} f(x) \phantom{x}dx + \int_{b}^{c} f(x) \phantom{x}dx &= [F(b) – F(a)] + [F(c) – F(b)]\\&= F(b) – F(a) + F(c) – F(b)\\&= F(c) – F(a) \end{aligned}Rewrite $F(c) – F(a)$ back into a definite integral.\begin{aligned}\int_{a}^{b} f(x) \phantom{x}dx + \int_{b}^{c} f(x) \phantom{x}dx&= F(c) – F(a)\\&= \int_{a}^{c} f(x) \phantom{x}dx \end{aligned}This confirms the definite integral property we use to combine intervals is indeed true.
Example 4Use the fact that the definite integrals of $f(x)$ and $g(x)$ have the following values with the lower and upper limits shown below:\begin{aligned}\int_{0}^{6} f(x) \phantom{x}dx &= 6\\\int_{0}^{3} f(x) \phantom{x}dx &= -2\\\int_{0}^{6} g(x)\phantom{x}dx &= -4\\ \int_{0}^{3} g(x) \phantom{x}dx &= 1\end{aligned}Compute the following definite integrals.a. $\int_{0}^{6} [f(x) + g(x)] \phantom{x}dx$
b. $\int_{0}^{3} [f(x) – g(x)] \phantom{x}dx$
c. $\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx$
d. $\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx$
e. $\int_{0}^{6} [2f(x) + 3g(x)] \phantom{x}dx$
f. $\int_{0}^{3} [3f(x) – 4g(x)] \phantom{x}dx$
g. $\int_{3}^{6} [2f(x) + 6g(x)] \phantom{x}dx$
SolutionApply the sum property of definite integrals, $\int_{a}^{b} [f(x) + g(x)]\phantom{x} dx = \int_{a}^{b} f(x)\phantom{x}dx + \int_{a}^{b} g(x)\phantom{x}dx$, to determine the value of $\int_{0}^{6} [f(x) + g(x)] \phantom{x}dx$.\begin{aligned}\int_{0}^{6} [f(x) + g(x)] \phantom{x}dx &= \int_{0}^{6} f(x)\phantom{x}dx + \int_{0}^{6} g(x)\phantom{x}dx \end{aligned}Use the given values for the two definite integrals to find the value of $\int_{0}^{6} [f(x) + g(x)] \phantom{x}dx$.a. This means that $\int_{0}^{6} [f(x) + g(x)] \phantom{x}dx$ is equal to $2$.We’ll apply a similar process to evaluate the definite integral, $\int_{0}^{3} [f(x) – g(x)] \phantom{x}dx$. This time, we’ll use the difference property of definite integrals, $\int_{a}^{b} [f(x) – g(x)]\phantom{x} dx = \int_{a}^{b} f(x)\phantom{x}dx- \int_{a}^{b} g(x)\phantom{x}dx$.\begin{aligned}\int_{0}^{6} [f(x) – g(x)] \phantom{x}dx &=\int_{0}^{6} f(x)\phantom{x}dx – \int_{0}^{6} g(x)\phantom{x}dx \\&= 6 – (-4)\\ &= 10 \end{aligned}b. Hence, $\int_{0}^{6} [f(x) – g(x)] \phantom{x}dx$ is equal to $10$.The given lower and upper limits of the definite integral, $\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx$, are the result of the four given definite integrals being combined. Rewrite $\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx$ in terms of the four given definite integrals and by applying the different properties for definite integrals.
- Use the sum property to distribute the definite integral operation.
- Expand $\int_{3}^{6} f(x)\phantom{x}dx$ and $\int_{3}^{6} g(x)\phantom{x}dx$ by reversing the process of combining a definite integral’s intervals, $\int_{a}^{b} f(x)\phantom{x}dx + \int_{b}^{c} f(x)\phantom{x}dx = \int_{a}^{c} f(x)\phantom{x}dx$.
- Reverse the limits of $\int_{3}^{0} f(x)\phantom{x}dx$ and $\int_{3}^{0} g(x)\phantom{x}dx$ using the reverse interval property, $\int_{a}^{b} f(x)\phantom{x}dx = -\int_{b}^{a} f(x) \phantom{x}dx$.
\begin{aligned}\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx &= \int_{3}^{6} f(x)\phantom{x}dx + \int_{3}^{6} g(x)\phantom{x}dx\\&=\left[\int_{3}^{0} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ] + \left[\int_{3}^{0} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ] \\&=\left[-\int_{0}^{3} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ] + \left[-\int_{0}^{3} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ]\\&=\left[\int_{0}^{6} f(x)\phantom{x}dx – \int_{0}^{3} f(x)\phantom{x}dx \right ] + \left[\int_{0}^{6} g(x)\phantom{x}dx -\int_{0}^{3} g(x)\phantom{x}dx \right ] \end{aligned}We’ve now expressed the definite integral in term of the following:\begin{aligned}\int_{0}^{6} f(x) \phantom{x}dx &= 6\\\int_{0}^{3} f(x) \phantom{x}dx &= -2\\\int_{0}^{6} g(x)\phantom{x}dx &= -4\\ \int_{0}^{3} g(x) \phantom{x}dx &= 1\end{aligned}We’ll substitute these values into our last expression to find the value of $\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx$.\begin{aligned}\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx &=\left[\int_{0}^{6} f(x)\phantom{x}dx – \int_{0}^{3} f(x)\phantom{x}dx \right ] + \left[\int_{0}^{6} g(x)\phantom{x}dx -\int_{0}^{3} g(x)\phantom{x}dx \right ] \\&= [6 – (-2)] + [-4 – (1)]\\&= 8 – 5 \\&= 3 \end{aligned}c. This means that $\int_{3}^{6} [f(x) + g(x)] \phantom{x}dx$ is equal to $3$.We’ll apply the same process to evaluate the fourth definite integral, $\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx$.\begin{aligned}\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx &= \int_{3}^{6} f(x)\phantom{x}dx – \int_{3}^{6} g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Difference Property}\\&=\left[\int_{3}^{0} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ] – \left[\int_{3}^{0} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ],\phantom{x}\color{Teal}\text{Combining Interval} \\&=\left[-\int_{0}^{3} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ] – \left[-\int_{0}^{3} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ],\phantom{x}\color{Teal}\text{Reverse Interval}\\&=\left[\int_{0}^{6} f(x)\phantom{x}dx – \int_{0}^{3} f(x)\phantom{x}dx \right ] – \left[\int_{0}^{6} g(x)\phantom{x}dx -\int_{0}^{3} g(x)\phantom{x}dx \right ] \end{aligned}Use the same values to determine the value of $\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx$.\begin{aligned}\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx &=\left[\int_{0}^{6} f(x)\phantom{x}dx – \int_{0}^{3} f(x)\phantom{x}dx \right ] – \left[\int_{0}^{6} g(x)\phantom{x}dx -\int_{0}^{3} g(x)\phantom{x}dx \right ]\\&= [6 – (-2)] – [-4 -(1)]\\&= 8 – (-5)\\&= 13 \end{aligned}d. Hence, we have $\int_{3}^{6} [f(x) – g(x)] \phantom{x}dx = 13$.Use the sum and difference property followed by the constant
multiple property to evaluate the next two definite integrals. Once we’ve rewritten the two definite integrals, substitute the given values into our new expression.
| \begin{aligned}\boldsymbol{\int_{0}^{6} [2f(x) + 3g(x)] \phantom{x}dx }\end{aligned} | \begin{aligned}\int_{0}^{6} [2f(x) + 3g(x)] \phantom{x}dx &= \int_{0}^{6} 2f(x)\phantom{x}dx +\int_{0}^{6} 3g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Sum Property}\\&= 2\int_{0}^{6} f(x)\phantom{x}dx + 3\int_{0}^{6} g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Property}\\&= 2(6) + 3(-4) \\&= 12 – 12\\&= 0\end{aligned} |
| \begin{aligned}\boldsymbol{\int_{0}^{3} [3f(x) – 4g(x)] \phantom{x}dx }\end{aligned} | \begin{aligned}\int_{0}^{3} [3f(x) – 4g(x)] \phantom{x}dx &= \int_{0}^{3} 3f(x)\phantom{x}dx – \int_{0}^{3} 4g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Difference Property}\\&= 3\int_{0}^{3} f(x)\phantom{x}dx-4\int_{0}^{3} g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Property}\\&= 3(-2) – 4(1) \\&= -6 – 4\\&= -10\end{aligned} |
This shows that through different definite integral properties, we can manipulate definite integrals to evaluate them and find their actual values. For our case, we have the following values:e. $\int_{0}^{6} [2f(x) + 3g(x)] \phantom{x}dx = 0$
f. $\int_{0}^{3} [3f(x) – 4g(x)] \phantom{x}dx = -10$The last definite integral that we need to evaluate is $\int_{3}^{6} [2f(x) + 6g(x)] \phantom{x}dx$. This is also a quick review to make sure you understand how we were able to evaluate and simplify the last five items.
- Apply the sum and constant multiple properties.
- Rewrite the integrals so they lower and upper limits that we can work with.
- Substitute the values that we know to simplify the expression and return an actual value.
\begin{aligned}\int_{3}^{6} [2f(x) + 6g(x)] \phantom{x}dx &= \int_{3}^{6} 2f(x)\phantom{x}dx + \int_{3}^{6} 6g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Sum Property}\\&=2\int_{3}^{6} f(x)\phantom{x}dx + 6\int_{3}^{6} g(x)\phantom{x}dx,\phantom{x}\color{Teal}\text{Constant Multiple Property}\\&=2\left[\int_{3}^{0} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ]+6\left[\int_{3}^{0} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ],\phantom{x}\color{Teal}\text{Combining Interval}\\&=2\left[-\int_{0}^{3} f(x)\phantom{x}dx +\int_{0}^{6} f(x)\phantom{x}dx \right ]+6\left[-\int_{0}^{3} g(x)\phantom{x}dx +\int_{0}^{6} g(x)\phantom{x}dx \right ],\phantom{x}\color{Teal}\text{Reversing Interval}\\&=2\left[\int_{0}^{6} f(x)\phantom{x}dx-\int_{0}^{3} f(x)\phantom{x}dx \right ]+6\left[\int_{0}^{6} g(x)\phantom{x}dx- \int_{0}^{3} g(x)\phantom{x}dx\right]\\&= 2[6 – (-2)] + 6[-4 – (1)]\\&= 2(8) + 6(-5)\\&= 16 – 30\\&= -14\end{aligned}g. This means that $\int_{3}^{6} [2f(x) + 6g(x)] \phantom{x}dx$ is equal to $-14$.
Example 5Show that $\int_{0}^{1} \sqrt{1 + 2x^4} \phantom{x}dx < 1.4$. Use the fact that $\int \sqrt{1 + x}\phantom{x} dx= \dfrac{1}{3}(1 + 2x)^{\frac{3}{2}} + C$.
SolutionSince we’re working with definite integrals with lower and upper limits at $x =0$ and $x =1$. Let’s evaluate the definite integral, $\int_{0}^{1} \sqrt{1 + x}\phantom{x} dx$ using the indefinite integral given from the problem.\begin{aligned}\int_{0}^{1} \sqrt{1 + 2x}\phantom{x} dx &= \dfrac{1}{3}(1 + 2x)^{\frac{3}{2}}|_{0}^{1}\\&= \dfrac{1}{3}[(1 + 2)^{\frac{3}{2}} -(1 + 0)^{\frac{3}{2}}]\\&= \dfrac{1}{3}(3^{\frac{3}{2}} – 1)\\& \approx 1.399\end{aligned}When $x$ is within the interval, $[0, 1]$, $x^4$ will be less than or equal to $x$. Let’s manipulate the inequality, $x^4 \leq x$, so that we end up comparing $\sqrt{1 + 2x^4} $ and $\sqrt{1 + 2x} $.\begin{aligned}x^4 &\leq x\\2x^4 &\leq 2x\\1 + 2x^4 &\leq 1 + 2x\\\sqrt{1 + 2x^4 }&\leq \sqrt{1 + 2x}\end{aligned}Now that we’ve shown that $\sqrt{1 + 2x^4} \leq \sqrt{1 + 2x}$, we can use the comparison property to estimate its value. Recall that when $f(x) \geq g(x) for $x \in [a, b]$, $\int_{a}^{b} f(x)\phantom{x}dx \geq \int_{a}^{b} f(x)\phantom{x}dx $.\begin{aligned} \sqrt{1 + 2x^4 }&\leq \sqrt{1 + 2x}\\\int_{0}^{1}\sqrt{1 + 2x^4 } \phantom{x} dx &\leq \int_{0}^{1}\sqrt{1 + 2x} \phantom{x} dx\\\int_{0}^{1}\sqrt{1 + 2x^4 } \phantom{x} dx &\leq \int_{0}^{1}\sqrt{1 + 2x} \phantom{x} dx < 1.4 \end{aligned}Hence, we’ve just shown that $\int_{0}^{1} \sqrt{1 + 2x^4} \phantom{x}dx < 1.4$.
Practice Questions
1. Use the fact that $\int_{0}^{8} f(x) \phantom{x} dx = -5$ and $\int_{-8}^{0} f(x) \phantom{x} dx = 35$ to determine the value of $\int_{-8}^{8} f(x) \phantom{x} dx$.2. Use the fact that $\int_{-2}^{1} g(x) \phantom{x} dx = 10$ and $\int_{1}^{2} g(x) \phantom{x} dx = -12$ to determine the value of $\int_{-2}^{2} g(x) \phantom{x} dx$.3. Use the fact that $\int_{0}^{5} f(x) \phantom{x} dx = -4$ and $\int_{0}^{12} f(x) \phantom{x} dx = -12$ to determine the value of $\int_{5}^{7} f(x) \phantom{x} dx$.4. Use the fact that $\int_{-2}^{4} g(x) \phantom{x} dx = 22$ and $\int_{-2}^{8} g(x) \phantom{x} dx = -5$ to determine the value of $\int_{4}^{8} g(x) \phantom{x} dx$.5. Prove the zero-length interval property, $\int_{a}^{a} f(x) \phantom{x}dx = 0$.6. Prove the difference property for indefinite integral, $\int_{a}^{b} [f(x) – g(x)] \phantom{x}dx = \int_{a}^{b} f(x) \phantom{x}dx – \int_{a}^{b} g(x) dx$.7. Use the fact that the definite integrals of $f(x)$ and $g(x)$ have the following values with the lower and upper limits shown below:
\begin{aligned}\int_{0}^{8} f(x) \phantom{x}dx &= 24\\\int_{0}^{4} f(x) \phantom{x}dx &= -12\\\int_{0}^{8} g(x)\phantom{x}dx &= -16\\ \int_{0}^{4} g(x) \phantom{x}dx &= 6\end{aligned}
Compute the following definite integrals.
a. $\int_{0}^{8} [f(x) + g(x)] \phantom{x}dx$
b. $\int_{0}^{4} [f(x) – g(x)] \phantom{x}dx$
c. $\int_{4}^{8} [f(x) + g(x)] \phantom{x}dx$
d. $\int_{4}^{8} [f(x) – g(x)] \phantom{x}dx$
e. $\int_{0}^{8} [4f(x) + g(x)] \phantom{x}dx$
f. $\int_{0}^{4} [6f(x) – 5g(x)] \phantom{x}dx$
g. $\int_{4}^{8} [12f(x) – 4g(x)] \phantom{x}dx$8. Use the fact that the definite integrals of $f(x)$ and $g(x)$ have the following values with the lower and upper limits shown below:
\begin{aligned}\int_{0}^{10} f(x) \phantom{x}dx &=-24\\\int_{0}^{5} f(x) \phantom{x}dx &= 12\\\int_{0}^{10} g(x)\phantom{x}dx &= 8\\ \int_{0}^{5} g(x) \phantom{x}dx &= -6\end{aligned}
Compute the following definite integrals.
a. $\int_{0}^{10} [f(x) + g(x)] \phantom{x}dx$
b. $\int_{0}^{5} [f(x) – g(x)] \phantom{x}dx$
c. $\int_{5}^{10} [f(x) + g(x)] \phantom{x}dx$
d. $\int_{5}^{10} [f(x) – g(x)] \phantom{x}dx$
e. $\int_{0}^{10} [f(x) + 6g(x)] \phantom{x}dx$
f. $\int_{0}^{5} [2f(x) – 3g(x)] \phantom{x}dx$
g. $\int_{5}^{10} [3f(x) + g(x)] \phantom{x}dx$9. Show that $\int_{0}^{1} \sqrt{1 + 4x^3} \phantom{x}dx < 1.7$. Use the fact that $\int \sqrt{1 + 4x}\phantom{x} dx= \dfrac{1}{6}(1 + 4x)^{\frac{3}{2}} + C$.10. Show that $\int_{0}^{1} \sqrt{2 + x^4} \phantom{x}dx < 1.6$. Use the fact that $\int \sqrt{2 + x}\phantom{x} dx= \dfrac{2}{3}(2 + x)^{\frac{3}{2}} + C$.
Answer Key
1. $\int_{-8}^{8} f(x) \phantom{x} dx = 30$
2. $\int_{-2}^{2} g(x) \phantom{x} dx = -2$
3. $\int_{5}^{7} f(x) \phantom{x} dx = -8$
4. $\int_{4}^{8} g(x) \phantom{x} dx = -27$
5.
If $F(x)$ is the antiderivative of $\int f(x)\phantom{x} dx$, we have the following:
$ \begin{aligned} \int_{a}^{b} f(x) \phantom{x}dx &= F(b) = F(a)\\\\\Rightarrow \int_{a}^{a} f(x)\phantom{x}dx &= F(a) – F(a)\\ &=0\end{aligned}$
This confirms the zero-length interval property for definite integrals, $\int_{a}^{a} f(x)\phantom{x} dx =0$.
6.
$\begin{aligned} \dfrac{d}{dx} [f(x) – g(x)] &= \dfrac{d}{dx}f(x) – \dfrac{d}{dx}g(x)\\\dfrac{d}{dx}\int f(x) dx &= f(x) \\\\\dfrac{d}{dx}\int[f(x) – g(x)] \phantom{x}dx&= f(x) – g(x)\\\dfrac{d}{dx}\left[\int f(x)\phantom{x}dx -\int g(x)\phantom{x}dx \right ]&= \dfrac{d}{dx}\int f(x)\phantom{x}dx -\dfrac{d}{dx}\int g(x)\phantom{x}dx\\&= f(x) – g(x)\\\Rightarrow \int [f(x) – g(x)]\phantom{x}dx &= \int f(x)\phantom{x}dx – \int f(x)\phantom{x}dx\end{aligned}$
7.
a. $\int_{0}^{8} [f(x) + g(x)] \phantom{x}dx = 8$
b. $\int_{0}^{4} [f(x) – g(x)] \phantom{x}dx = -18$
c. $\int_{4}^{8} [f(x) + g(x)] \phantom{x}dx = 14$
d. $\int_{4}^{8} [f(x) – g(x)] \phantom{x}dx = 58$
e. $\int_{0}^{8} [4f(x) + g(x)] \phantom{x}dx = 80$
f. $\int_{0}^{4} [6f(x) – 5g(x)] \phantom{x}dx = -102$
g. $\int_{4}^{8} [12f(x) – 4g(x)] \phantom{x}dx = 520$
8.
a. $\int_{0}^{10} [f(x) + g(x)] \phantom{x}dx = -16$
b. $\int_{0}^{5} [f(x) – g(x)] \phantom{x}dx = 18$
c. $\int_{5}^{10} [f(x) + g(x)] \phantom{x}dx = -22$
d. $\int_{5}^{10} [f(x) – g(x)] \phantom{x}dx = -50$
e. $\int_{0}^{10} [f(x) + 6g(x)] \phantom{x}dx = 24$
f. $\int_{0}^{5} [2f(x) – 3g(x)] \phantom{x}dx = 42$
g. $\int_{5}^{10} [3f(x) + g(x)] \phantom{x}dx = -94$
9.
$\begin{aligned}\int_{0}^{1} \sqrt{1 + 4x}\phantom{x} dx &\approx 1.697\\\\\ x^3 &\leq x\\\sqrt{1 + 4x^3} &\leq \sqrt{1 + 4x}\\\int_{0}^{1}\sqrt{1 + 4x^3} \phantom{x}dx &\leq \int_{0}^{1}\sqrt{1 + 4x} \phantom{x}dx\\\int_{0}^{1} \sqrt{1 + 4x^3}\phantom{x}dx &< 1.7\end{aligned}$
10.
$ \begin{aligned}\int_{0}^{1} \sqrt{2 + x}\phantom{x} dx &\approx 1.578\\\\\ x^4 &\leq x\\\sqrt{2 + x^4} &\leq \sqrt{2 + x}\\\int_{0}^{1}\sqrt{2 + x^4} \phantom{x}dx &\leq \int_{0}^{1}\sqrt{2 + x} \phantom{x}dx\\\int_{0}^{1} \sqrt{2 + x^4}\phantom{x}dx &< 1.6\end{aligned}$