
The main objective of this question is to check whether the addition of the given two functions when both the functions are odd, even
or one is odd and the other is even results in even or odd function.
Even
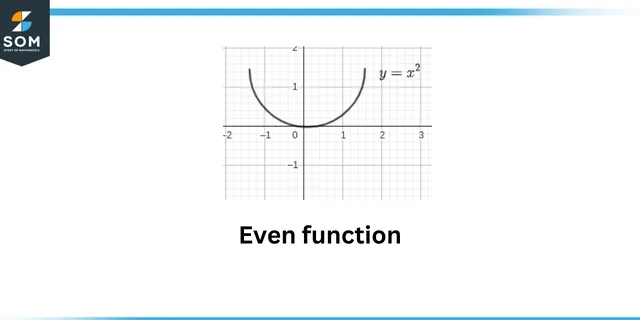
Even function
This question shows the concept of even and odd functions. An even function is mathematically represented as:
\[f(-x) = f(x)\]
While the odd function is mathematically represented as:
\[f(-x) = -f(x)\]
Odd function
Expert Answer
We have to show that the given two functions which are $ f $ and $ g$ are even or odd.
Let:
\[h(x) \space = \space f(x) \space + \space g(x) \]
An even function is mathematically represented as $ f(-x) \space = \space f(x) $ while the odd function is mathematically represented $ f(-x) \space = \space -f(x) $.
Suppose that the given two functions which are $ f $ and $ g$ are even functions, then:
\[h(-x) \space = \space f(-x) \space + \space g(-x) \]
\[h(x) \space = \space f(x) \space + \space g(x) \]
Thus, $ h $ is an even function.
Now suppose that the given two functions which are $ f $ and $ g$ are odd functions, then:
\[h(-x) \space = \space f(-x) \space + \space g(-x) \]
\[ = \space – f(x) \space + \space -g(x) \]
\[ = -( f(x) \space + \space g(x) )\]
\[ -h(x) \space = \space – ( f(x) \space + \space g(x) )\]
Thus $ h $ is an odd function.
Now from the given two functions, one function is odd and the other is even, so:
\[h(-x) \space = \space f(-x) \space + \space g(-x) \]
\[h(-x) \space = \space f(x) \space + \space g(-x) \]
\[h(-x) \space = \space f(x) \space – \space g(-x) \]
This $ h$ function is neither even nor odd.
Numerical Answer
- When the two functions are odd, then the sum of two functions results in an odd function.
- When the two functions are even, then the sum of two functions results in an even function.
- When two functions are given; one is odd and the other is even, then their sum will result in neither an even nor odd function.
Example
When the two functions $ a $ and $ b $ are even, then the production of these two function will result in even or odd function.
We know that an even function is mathematically represented as:
\[f(-x) = f(x)\]
While the odd function is mathematically represented as:
\[f(-x) = -f(x)\]
So,Let:
\[f \space : \space A \space \rightarrow \space f(x)\]
This is an even function then:
\[f(-x) \space = \space f(x)\]
Also, let $
\[g \space : \space B \space \rightarrow \space f(x)\]
This is an even function then:
\[g(-x) \space = \space g(x) \]
Let:
\[h \space = \space h . g \]
\[h(-x) \space = \space (f.g)(-x) \space = \space f(-x)g(-x) \space = \space f(x)g(x) \space = \space h(x)\]
Thus, when the two given functions are even then their product will also result in an even function.
