Identity Matrix – Explanation & Examples

Identity matrices are just the matrix counterpart of the real number $ 1 $. They have some interesting properties and uses in matrix operations. Let’s check the formal definition of what an identity matrix is first:

An Identity Matrix is a square matrix of any order whose principal diagonal elements are all ones and the rest other elements are all zeros.

In this lesson, we will look at what identity matrices are, how to find different identity matrices, some properties of identity matrices, and the determinant of an identity matrix.

Towards the end, we will show some examples to clarify your understanding of identity matrices and some practice problems for you to practice. Let’s get started!

What is an Identity Matrix?

An identity matrix is a square matrix in which all the elements in its principal diagonal are $ 1 $s, and the rest of the elements are $ 0 $s. The principal diagonal is the diagonal line of the square matrix that runs from top-left to bottom-right. 

The identity matrix plays a similar role to the real number $ 1 $ in the domain of operations with matrices. We will see how, later. We denote an identity matrix by $ I_{n} $ where $ n $ is the order of the square matrix. Identity matrices are also known as a unit matrix or elementary matrix. Below, we will see how we find identity matrices of different orders.

How to find Identity Matrix

We can have identity matrices of any order. We come across the most common ones: first order, second order, third order, and fourth order. Below, we see these:

$ I_{ 1 } = \begin {bmatrix} 1 \end {bmatrix} $

This is the simplest identity matrix. This is of the order $ 1 $. It is denoted as $ I_{ 1 } $.

$ I_{ 2 } = \begin{bmatrix} { 1 }  & { 0 } \\ { 0 } & { 1 }  \end {bmatrix} $

This is an identity matrix of the order $ 2 $. It is denoted as $ I_{ 2 } $.

$ I_{ 3 } = \begin{bmatrix} { 1 }  & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 1 }  \end {bmatrix} $

This is an identity matrix of the order $ 3 $. It is denoted as $ I_{ 3 } $.

$ I_{ 4 } = \begin{bmatrix} { 1 }  & { 0 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 1 }  \end {bmatrix} $

This is an identity matrix of the order $ 4 $. It is denoted as $ I_{ 4 } $.

We can have similar identity matrices of order $ 5 $, $ 6 $, $ 7 $, and any number until $ n $.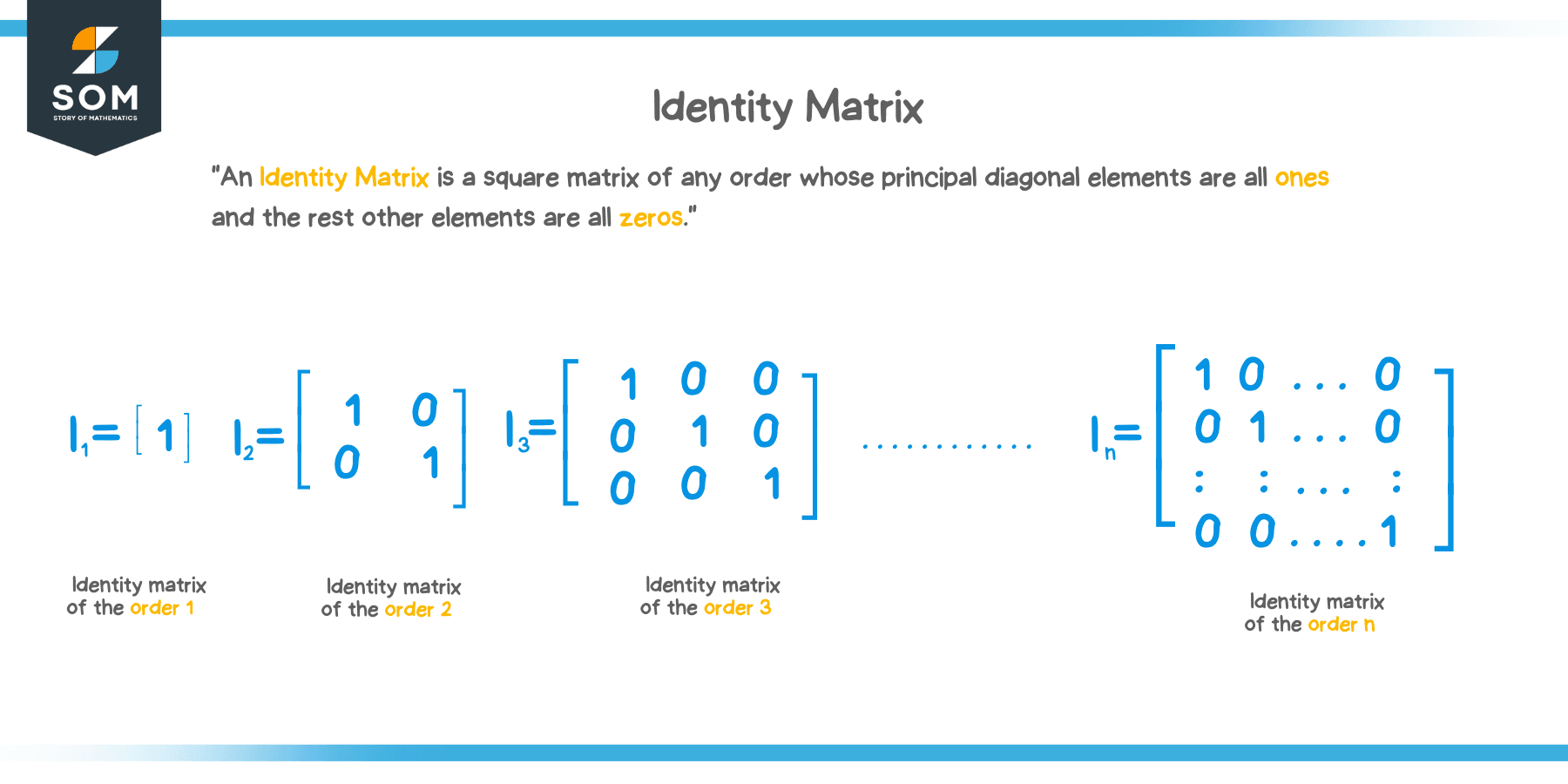

How are identity matrices important in the field of matrices? What are their properties? Let’s have a look below.

Identity Matrix Properties

Let’s take a look at $ 4 $ properties of identity matrices below:

1. An identity matrix is always a square matrix.

   As you have already seen above, all of the identity matrices shown are square matrices, meaning that the number of rows and columns are equal. From the definition of an identity matrix, it follows that identity matrices will have to be a square matrix!

2. Multiplying a matrix with an identity matrix will result in the non-identity matrix itself.

   If we multiply matrix $ A $ by the compatible identity matrix $ I $, we will have the matrix itself.
   $ AI = A $
   $ IA = A $

   Please note: To multiply a matrix by the compatible identity matrix, we must keep in mind the matrix multiplication rules. Whether we are putting the matrix first or the identity matrix first, we have to remember that the number of columns of the first matrix needs to be equal to the number of rows of the second matrix. Only then, the matrix multiplication process will be defined. To read more about matrix multiplication, please click here.

3. Multiplying a matrix by its inverse will result in an identity matrix of the same order. We will leave out the matrix inverse topic for now, but if you want to know how to take the inverse of a matrix, please check here.
   $ A * A^{ – 1 } = I $

   Note: The matrices involved in this multiplication are known as multiplicative inverses of each other.

4. The trace of an identity matrix is equal to $ n $, the identity matrix’s order.

   Recall that the trace of a matrix is the sum of all the elements in its principal diagonal. Since an identity matrix has only $ 1 $s in each of its diagonal elements, there are $ n $ ones in total.
   Thus, there are $ n $ ones. The sum would definitely be $ n $. 

   The trace is equal to $ n $, the order of the identity matrix we are concerned with!

5. The determinant of an identity matrix is always equal to $ 1 $. We will look at this topic next.

Determinant of an Identity Matrix 

What exactly is the determinant of a matrix?

The determinant of a matrix is a scalar value that results from some operations with the elements of a matrix. In high-school level mathematics, we are primarily concerned with determinant of $ 2 \times 2 $ matrices and $ 3 \times 3 $ matrices. Remember, we can only find the determinant of a square matrix. 

Consider the $ 2 \times 2 $ matrix shown below:

$ A = \begin{bmatrix} { a }  & { b } \\ { c } & { d }  \end {bmatrix} $

The determinant of this matrix can be denoted by the notations $ | A | $ or $ det( A ) $. The formula for the determinant of a $ 2 \times 2 $ matrix is:

$ det( A ) = | A | = ad – bc $

Now, let’s write the $ 2\times 2 $ identity matrix:

$ I_{ 2 } = \begin{bmatrix} { 1 }  & { 0 } \\ { 0 } & { 1 }  \end {bmatrix} $

Let’s use the determinant of a $ 2 \times 2 $ matrix formula to find the determinant of a $ 2 \times 2 $ identity matrix. The process is shown below:

$ I_{ 2 } = \begin{bmatrix} { 1 }  & { 0 } \\ { 0 } & { 1 }  \end {bmatrix} $
$ det( I_{ 2 } ) = | I_{ 2 } | = ( 1 )( 1 ) – ( 0 )( 0 ) = 1 $

The determinant of the identity matrix is 1! This confirms property # 5 from above. Now, let’s take a look at the determinant of a $ 3 \times 3 $ matrix.

Consider the $ 3 \times 3 $ matrix shown below:

$ B = \begin{bmatrix} { a }  & { b } & { c } \\ { d } & { e } & { f } \\ { g } & { h } & { i }  \end {bmatrix} $

The formula for the determinant of a $ 3 \times 3 $ matrix is:

$ det( B ) = | B | = a \begin{vmatrix} { e } & { f } \\ { h } & { i } \end{vmatrix} – b \begin{vmatrix} { d } & { f } \\ { g }  & { i } \end{vmatrix} + c \begin{vmatrix} { d } & { e } \\ { g } & { h } \end{vmatrix}  $

Note: We have $ a $ times the determinant of the remaining matrix (denoted with ” | ” and ” | ” ) minus b times the determinant of the remaining matrix plus c times the determinant of the remaining matrix. The determinant of the remaining matrix will be calculated using the $ 2 \times 2 $ matrix determinant formula. If you want to know more about the formula, please check this article out! 

The $ 3 \times 3 $ identity matrix is shown below:

$ I_{ 3 } = \begin{bmatrix} { 1 }  & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 1 }  \end {bmatrix} $

Now, let us use the determinant of a $ 3 \times 3 $ matrix formula shown above to find the determinant of a $ 3 \times 3 $ identity matrix. The process is shown below:

$ I_{ 3 } = \begin{bmatrix} { 1 }  & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 1 }  \end {bmatrix} $
$ det( I_{ 3 } ) = | I_{ 3 } | = 1 [ ( 1 )( 1 ) – ( 0 )( 0 ) ] – 0 [ ( 0 )( 1 ) – ( 0 )( 0 ) ] + 0 [ ( 0 )( 0 ) – ( 0 )( 1 ) ] $
$ = 1 [ 1 – 0 ] – 0 [ 0 – 0 ] + 0 [ 0 – 0 ] $
$ = 1 [ 1 ] = 1 $

The determinant of the identity matrix is 1! This confirms property # 5 from above. Likewise, if we were to compute the determinant of a $ 4 \times 4 $ identity matrix, or a $ 5 \times 5 $ identity matrix, we will still get the answer, $ 1 $!

Let’s take a look at some examples for this lesson.

Example 1

Which of the following matrices is an identity matrix?

$ A = \begin{bmatrix}  { 1 }   & { 0 }  \\  { 0 }  &  { 1 }   \end {bmatrix} $
$ B = \begin{bmatrix}  { 1 }  & { 0 }  &  { 0 }  & { 0 } \\ { 0 }  &  { 1 }  & { 0 }  & { 0 }  \\ { 0 }  & { 0 }  & { 1 }  & { 0 } \end {bmatrix} $
$ C = \begin{bmatrix}  { 5 }   & { 0 }  & { 0 }  \\  { 0 }  &  { 5 } & { 0 }  \\ { 0 }  & { 0 }  & { 5 }  \end {bmatrix} $

Solution

Matrix $ A $ is clearly a $ 2 \times 2 $ identity matrix.

Matrix $ B $ looks like an identity matrix at first, but actually, it’s not. It is not even a square matrix. So, this isn’t an identity matrix.

Matric $ C $ doesn’t have $ 1$s in its diagonal elements, so it’s not an identity matrix.

Example 2

Given,

$ A = \begin{bmatrix}  2   & -1  \\  0  &  3   \end {bmatrix} $

Find $ I_{2} * A $.

Solution

We need to multiply the $ 2 \times 2$ identity matrix with matrix $A$. From our properties of identity matrices, we already know that the answer is going to be matrix $ A$. Let’s show the multiplication:

$I_{2} * A = \begin{bmatrix}  1   & 0  \\  0  &  1   \end {bmatrix} * \begin{bmatrix}  2   & -1  \\  0  &  3   \end {bmatrix} $

$ = \begin{bmatrix}  (1)(2) + (0)(0)   & (1)(-1) + (0)(3)  \\  (0)(2) + (1)(0) &  (0)(-1) + (1)(3) \end {bmatrix} $

$ = \begin{bmatrix}  2   & -1  \\  0 &  3 \end {bmatrix} $

In fact, $ I_{2} * A = A $.

Now, it’s your turn to try out some questions.

Practice Questions

1. Are $  A = \begin{bmatrix}  { – 2 }   & 4 \\  1  &  2   \end {bmatrix} $ and $ B = \begin{bmatrix}  {- \frac{1}{4} }   & { \frac{1}{2} }  \\  { \frac{1}{8} }  &  { \frac{1}{4} }  \end {bmatrix}$ multiplicative inverses of each other?

2. For a $ 7 \times 7 $ identity matrix, find the determinant and trace of the matrix.

Answers

1. If $ A * B = I $, then Matrix $ A $ and Matrix $ B $ are multiplicative inverses of each other. Let’s perform the multiplication and see.

   $ A * B = \begin{bmatrix}  -2   & 4 \\  1  &  2   \end {bmatrix} * \begin{bmatrix}  {- \frac{ 1 }{ 4 } }   & \frac{ 1 }{ 2 }  \\  \frac{ 1 }{ 8 }  &  \frac{ 1 }{ 4 }  \end {bmatrix} $

   $ = \begin{bmatrix}  (-2)(-\frac{ 1 }{ 4 } ) + (4)(\frac{ 1 }{ 8 } )   & (-2)(\frac{ 1 }{ 2 } ) + (4)(\frac{ 1 }{ 4 } )  \\  (1)(- \frac{ 1 }{ 4 } ) + (2)(\frac{ 1 }{ 8 } ) &  (1)(\frac{ 1 }{ 2 } ) + (2)(\frac{ 1 }{ 4 } ) \end {bmatrix} $

   $ = \begin{bmatrix}  1   & 0  \\  0 &  1 \end {bmatrix} $

   Since the answer is a $ 2\times2 $ identity matrix, we can conclude that Matrix A and Matrix B are multiplicative inverses of each other.

2. From the properties of identity matrices, we know that no matter the order of an identity matrix, the determinant is always equal to $ 1 $. The trace is equal to $ n $.

   For a $ 7 \times 7 $ identity matrix:

   The determinant is equal to 1.
   The trace is equal to 7.

Previous Lesson | Main Page | Next Lesson