JUMP TO TOPIC

Solid|Definition & Meaning

Definition

Any three-dimensional object is generally called a solid. These are shapes as we perceive them around us. Unlike 2D shapes, solids have the third dimension of depth in addition to length and width, which leads to the concept of volume. Pyramids, cylinders, cubes, spheres, etc., are all examples of solid 3D shapes, and their study is called Solid Geometry.

Solids form the basis of a field of geometry called Solid Geometry. It is slightly different from traditional geometry in the sense that the third dimension raises a degree of complexity. Some well-known solids include pyramids, cubes, rectangular prisms, spheres, cones, and cylindrical objects, etc. These objects are shown in the figure below:

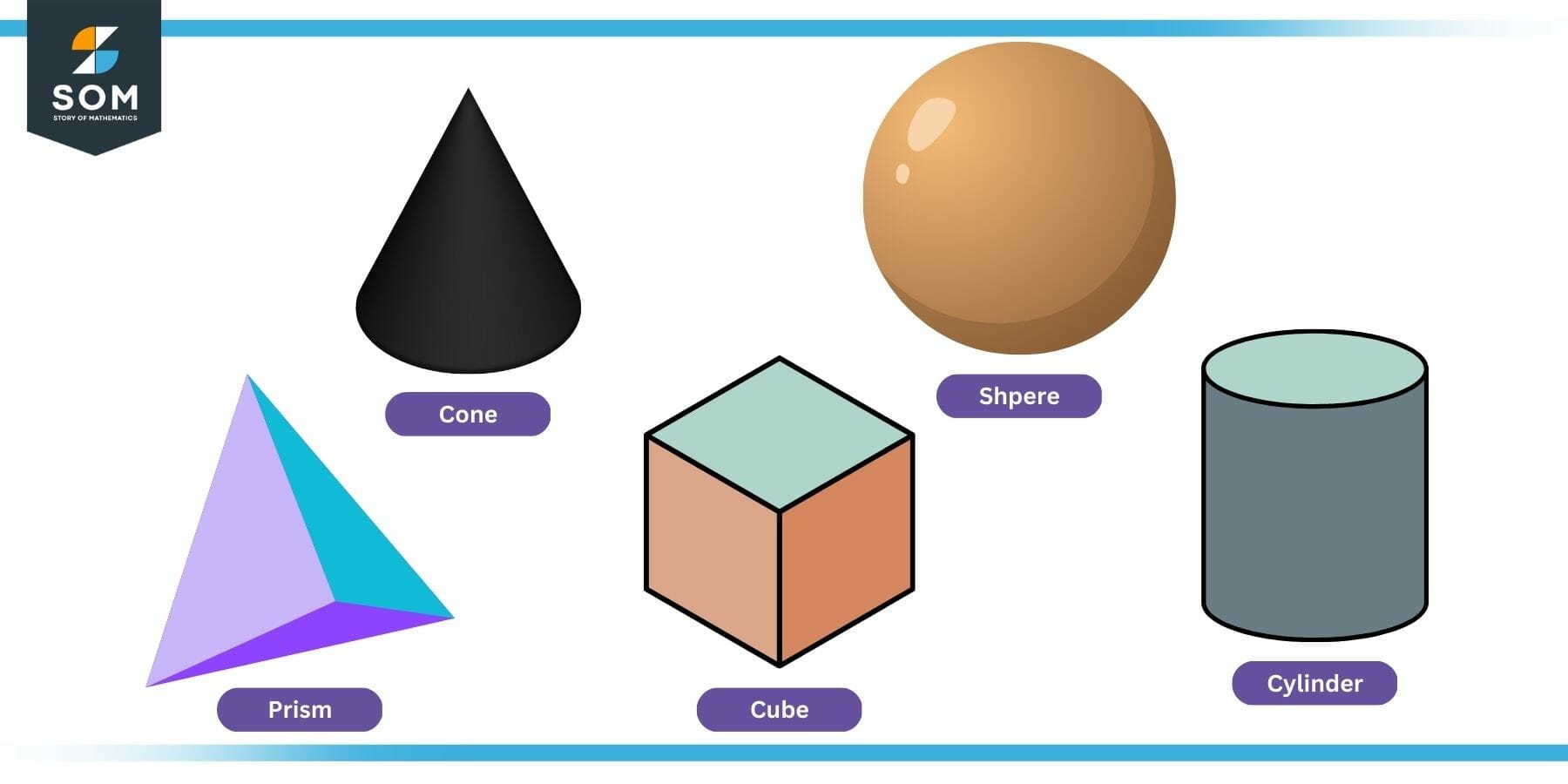
Figure 1: Examples of Solids

Explanation of Solids

As explained earlier, solids are a class of three-dimensional objects having length, breadth, and height (names of the three dimensions). If someone already has a background in two-dimensional shapes such as circles, squares, triangles, etc.

Such solid shapes may seem complex at first glance. However, with a little intuition, one can see the relationship between both domains and realize that three-dimensional geometry or solids can be explained directly from the two-dimensional counterpart.

To elaborate on this concept further, let us consider an example. The following figure shows a sphere (that is a solid).

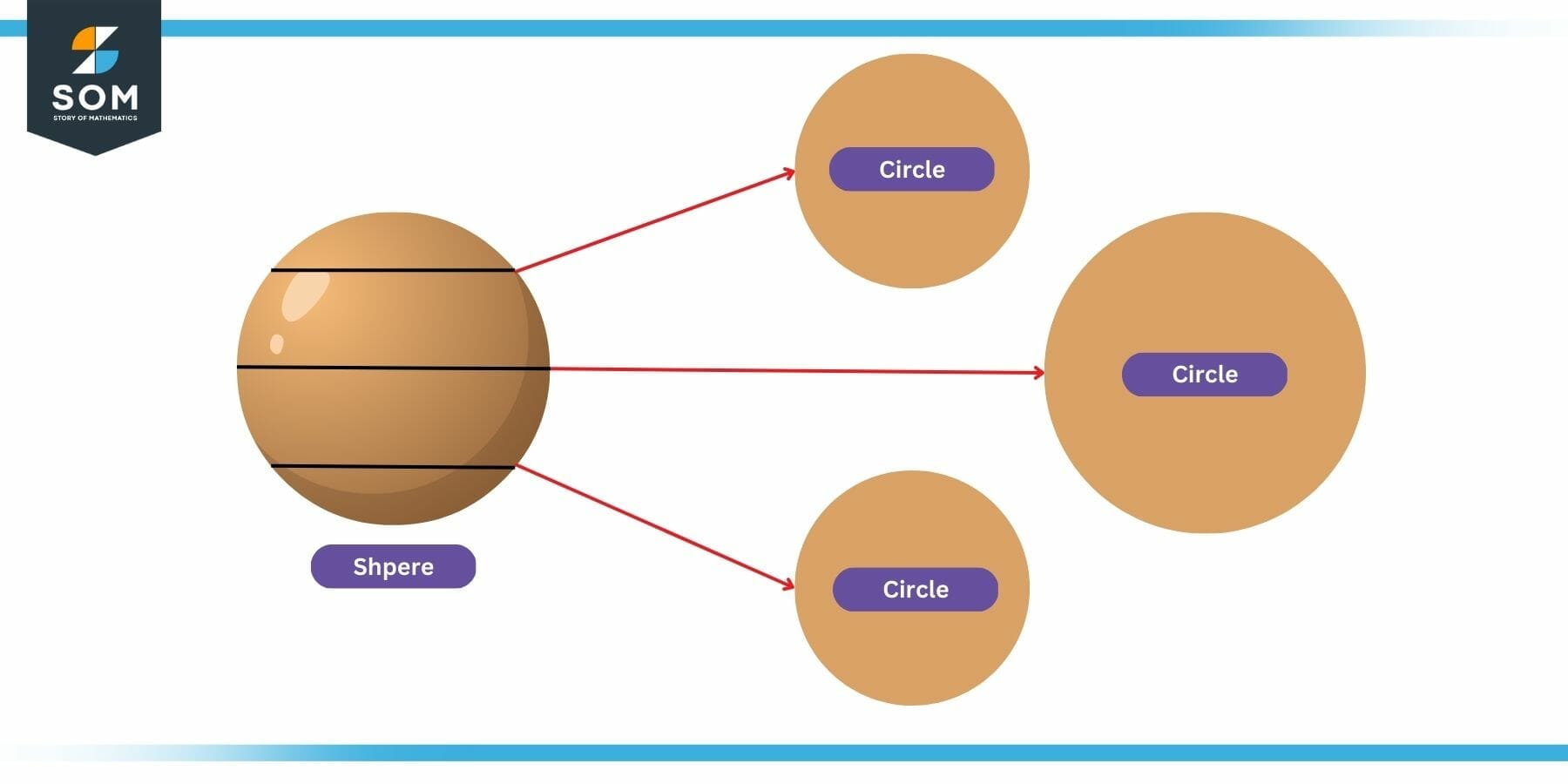
Figure 2: Relation between Solids and 2D Shapes

Now if we slice the sphere at three locations, as shown in the figure, and then see the cross-section of the object. We will see that these cross sections are a two-dimensional shape. It turns out that it’s a circle. We may generalize from this example that if we slice any solid object along any one of the three dimensions, the resulting shape would be a two-dimensional shape.

The above concept is very fundamentally vital for deriving expressions and formulae of different characteristics of solid objects. Let us consider this same concept, but now, let us learn by way of mathematical expressions.

Consider the equation of a unit circle (radius = 1) at origin (center at origin) in 2D (xy plane):

x² + y² = 1

The equation of a solid sphere with a unit radius (radius = 1) located at the origin in 3d (xyz space) is shown below:

x² + y² + z² = 1

Comparing the above two equations, can you guess the relationship between a circle and a sphere? Yes, it is very intuitive. Two statements can be deducted from these formulae.

First, the 2D shape (circle) is a subset of the 3D solid (sphere), which can be obtained by dropping any one of the dimensions. Second, the expressions for 2D shapes can be extended to 3D solids by adding another dimension. However, the latter mapping is a one-to-many relationship and would not have a unique solution.

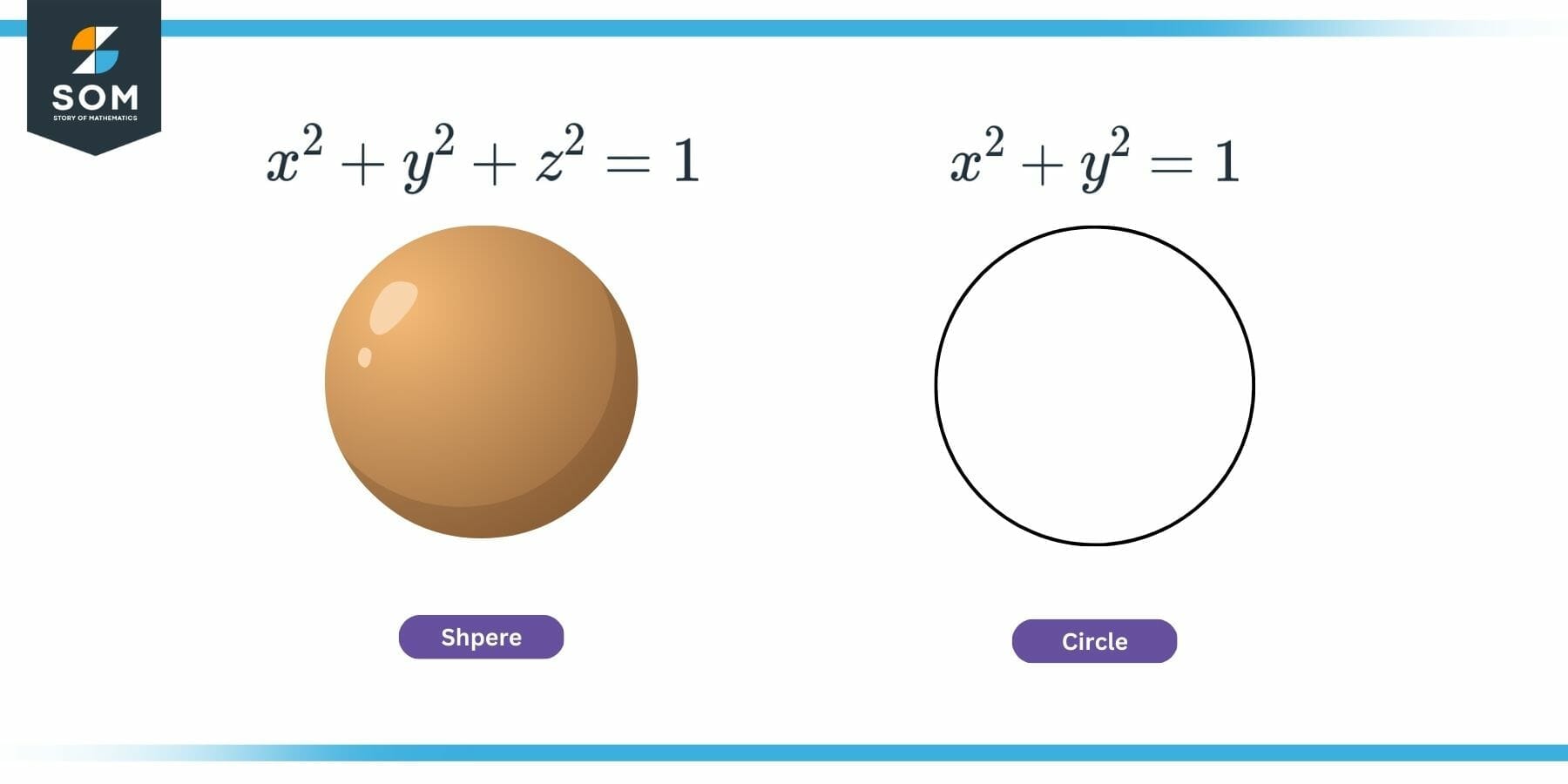
Figure 3: Equation of a Sphere and a Circle

The characteristics of these solid objects, such as the number of faces, vertices, edges, etc., may be frequently found in the literature. So one may need to understand all these basic terminologies to grasp some higher-level concepts.

Examples and visual depictions of solids in the form of diagrams and figures can assist beginners in understanding such objects and developing the basic intuition that is existential for working with them.

Other than basic solids (spheres, cubes, cones, etc.), several other complicated forms are not that easy to remember and may only be explained mathematically. Such objects are usually illustrated with the help of 3D rendering software such as AutoCAD and SketchUp.

Applications of Solids

Although we are more concerned with 2D shapes in our mathematics courses but the real world is 3D, and to build anything useful with real-world applications, we have to understand solid geometry. Solids find applications in many fields of engineering and art.

Architecture, Physics, and Graphics are the most significant among these. Engineers may construct and test prototypes while architects use them to plan and visualize architectural ideas.

Figure 4: Application of Solids

Some Common Characteristics of Solids

When studying solid shapes, it is essential to comprehend the properties of solids and how they may be mathematically stated. Solid shapes are, after all, three-dimensional objects with length, width, and height. They may be distinguished by their characteristics, such as the number of faces, vertices, and edges, and the knowledge of these terms is crucial for their applications in many areas.

Following are some of the important and commonly used terminologies:

Volume: Volume is the amount of space a solid shape takes up. It is very commonly used, and standard formulae exist for standard solid models.
Surface Area: Surface area is the total area of all of a solid shape’s faces.
Cross-Sectional Area: The area of any slice or cross-section of a solid object is called the cross-sectional area.
Edges: Line segments that connect two of its faces or vertices are called edges of a solid body.
Vertices: The point of intersections on a solid body where two or more edges meet are called vertices.
Faces: The flat surfaces or regions comprising points with the same surface normal are called the faces of the solid object.
Radius: For spherical or circular areas of a solid body, the radius is defined as the distance between the circumferential points and the center of the circle or sphere.

There are also other, more advanced terms, but these are enough at this level.

Some Elementary Solids

Let us consider some of the elementary solids in detail.

Solid Cube

A cube has six square faces, eight vertices, and twelve edges. They are one of the easiest solid objects to work with, and because of their three-dimensional construction, they are frequently used as building blocks and toys.

Rectangular Box

Rectangular prisms can have any configuration of rectangles on their faces, much like cubes. Similar to each other, these objects contain eight vertices and twelve edges. Rectangular prisms may be used to replicate genuine objects like furniture and buildings as well as boxes and containers.

Solid Sphere

Spheres are round objects with no vertices or edges. Instead, their center and radius operate as distinguishing features. Because they have a smooth, continuous surface, spheres are commonly used to symbolize objects like planets and basketballs.

Solid Cones

A cone’s base is circular and has a single vertex. The cone’s axis, which has one flat face and one curved face, runs from the vertex to the center of the base. Cones are used to mimic a range of objects, such as ice cream cones and party hats.

Cylinders

Cones and cylinders are related; however, cones only have one curved face, whereas cylinders have two parallel faces. The route that joins the centers of the two circular faces is known as the cylinder’s axis. Cylinders are used to create models for objects like cans and tubes.

Daily Life Examples of Solids

As referenced earlier, the following are some examples of real-world solids:

Solid Cube: Lego building blocks and toys
Rectangular Box: Packaging boxes and containers
Solid Sphere: planets and basketballs
Solid Cones: Ice cream cones and party hats
Cylinders: Cans and tubes

Of course, there are many others.

Numerical Problems of Solids

(a) Calculate the volume of a cylinder with a height of 6 cm and a radius of 3 cm.

(b) Calculate the volume of a sphere with a radius of 3 cm.

Solution

Part (a): Volume of a Cylinder

The formula for a cylinder’s volume is as follows:

V = πr²h

where h is the height and r is the radius. Substituting given values:

V = 3.14 x (3 cm)² (6 cm)

V = 3.14 x 9 x 6 cubic centimeters

V = 169.56 cubic centimeters

The cylinder’s volume is 169.56 cubic centimeters.

Part (b): Volume of a Sphere

The formula for a sphere’s volume is as follows:

V = (4/3)πr³

where r is the radius. Substituting given values:

V = (4/3) (3.14) (3 cm)³

V = 113.1 cubic centimeters

The sphere’s volume is 113.1 cubic centimeters.

Part (c): Volume of a Cone

The formula for a cone’s volume is as follows:

V = πr²h/3