JUMP TO TOPIC
Segment|Definition & Meaning
Definition
In geometry, the term segment means one of two things: part of a line (a line segment) or one of the two parts of a circle when it is split by a line or a chord of that circle (a circular segment). However, since a line segment is part of a line, it only has length, whereas the circular segment has two lengths (the lengths of the arc and the cutting chord) and therefore has some area.
A portion of a line that is defined by having two ends and a consistent length is referred to as a line segment. It differs from a line that has neither a beginning nor an end and can be stretched in both directions.
In the field of geometry, the line segment is generally defined as the portion of a line that is enclosed by 2 different points on the line. Alternatively, we may say that a line segment is a finite portion or part of a line that lies between two points.
A line does not have any endpoints and can extend infinitely in either direction. However, a line segment has two endpoints that are fixed or definite in some way. The characteristic that differentiates a ray from a line segment is the fact that a ray only has one endpoint, while the other end of the ray extends indefinitely.
A line is a shape that only exists in one dimension and is made up of a collection of points that go on forever in either direction. One can see a line depicted in the following figure.
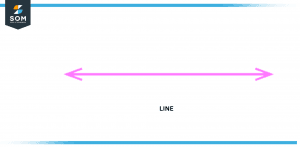
Figure 1 – Line
A line segment has two ends and is the part of the line that has the smallest distance between those endpoints. A line segment is depicted in the figure that can be found below.
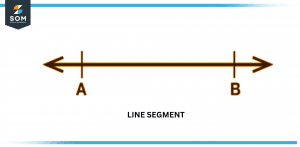
Figure 2 – Line Segment
Representation of Segment or Line Segment
Typically, the symbol for the segment is a bar (—) which is placed on top of the endpoints of a line segment to denote its representation. If a line segment, for example, has endpoints P and Q, it can be represented as $\mathsf{\overline{PQ}}$
The Formula for Line Segments
A line segment, as we are aware, has two endpoints. Now that we have the starting and ending points, we can use the distance calculation to get the exact length of a line segment.
\[ d = \sqrt {\left( {x_1-x_2 } \right)^2 + \left( {y_1-y_2 } \right)^2 } \]
Properties
Some properties of the line segment are mentioned below.
- The line segment is terminated at two different spots. This indicates that its ends are immovable.
- Since the line segment does have a set of endpoints, its length is fixed. In order to facilitate accurate length measurement.
- The sign for such a line segment is a dash, which may be written as (——).
- A portion of the line that contains a collection of endpoints is referred to as a line segment.
The line segment is a one-dimensional object: it has no thickness, only length. It serves as a basic building block for 2D and 3D shapes.
Examples of Line Segments in the Real World
A few examples of line segments from the real world are:
- Table’s edges
- A square or triangle’s side
- A ruler’s edge or a pencil
There are many others, as you can probably guess.
Line Segment Measurement
How should one go about measuring a certain line segment? There will be a variety of teaching styles utilized here.
Simply by Watching
The way of comparing two line segments that require the least amount of effort is to simply observe them side by side. By looking at two different line segments, one might determine whether one is longer or shorter in relation to the other.
In the illustration that was just presented, we can deduce from the simple observation that the length of a line segment represented by CD is bigger than the length of a line segment AB. However, this technique has a number of limitations, and we cannot rely solely on observation in order to do a comparison between two line segments.
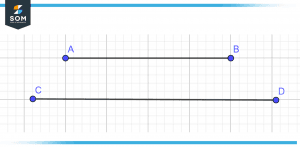
Figure 3 – Illustration of a line segment
Utilizing a Trace Paper
Two different line segments can indeed be compared in a straightforward manner using trace paper. If you follow the path of one line segment & superimpose it on the other, you will quickly be able to determine which one is the longer of the two. When working with more than 2 line segments, you will need to repeat the operation multiple times.
Accurate tracing of the line segments is required in order to conduct precise comparisons. Because of this, the success of this method is dependent on the precision of the tracing, which is a restriction placed on this method.
Using a Divider and a Ruler
The ruler (or scale) has certain markings that start at zero and divide its length into equal portions, usually in centimeters (cm). These unit centimeters are further divided into 10 parts, each of which is equal to 1 millimeter in length. You can use it to draw line segments of corresponding lengths from the 0 cm mark to the x cm mark, where x is the required length of the line segment.
What Is the Midpoint of a Segment?
The point on a line segment that is exactly halfway between two other congruent points on the line is known as the midpoint of that segment.
What Is the Bisector of a Segment?
A line, ray, line segment, or point that splits a line segment in half at its center is known as a segment bisector. The term “segment” can also be used to refer to a line segment, which designates a section of a line with defined ends. A line or other object can be bisected to create two equal halves.
Consequently, a segment bisector is what happens when two line segments cut or bisect each other at a point that divides the lines into equal halves.
What Is a Congruent Segment?
A pair of line segments that really are identical in terms of their length is referred to as congruent segments. A line segment is just a section of a line that is straight and has a distinct beginning point and an ending point. Because a line segment has a beginning and an ending point, its length can indeed be measured, and we can compare the two in its terms.
On the other hand, a line can be drawn continuously in either direction, which means that there is no end or start to it, whereas a ray has a specific beginning point but an unknown ending point. Both of these cannot be differentiated on the basis of their length as it extends to infinity.
Numerical Examples of a Segment
Example 1
Count how many line segments there are in the given figure.
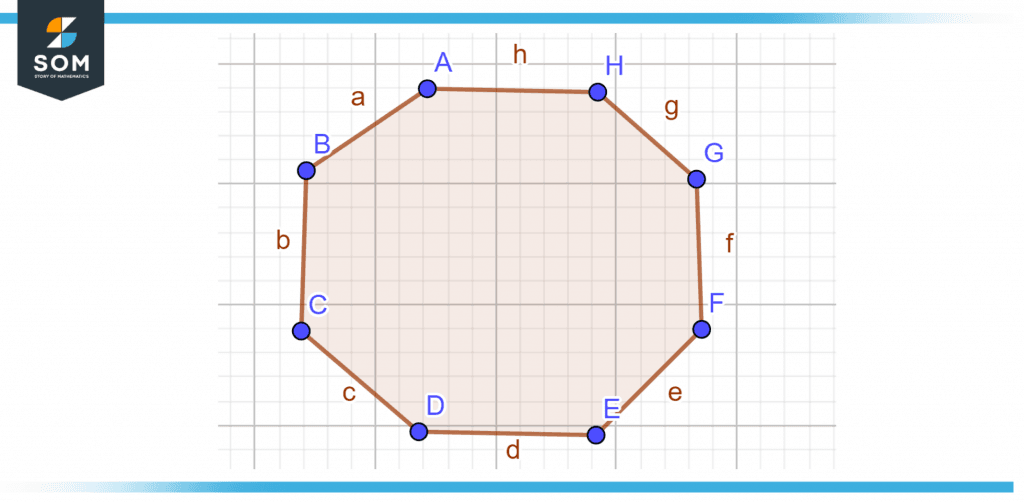
Figure 4 – Find the line segments on this shape (hint: it’s an octagon).
Solution
Eight line segments make up the presented figure.
Example 2
Find the length of a line segment between the coordinates of (2, –3) and (–1, –2).
Solution
Given that:
The coordinates are (2, –3) and (–1, –2)
We have to find the segment’s length. We know that the distance formula is:
\[ d = \sqrt {\left( {x_1-x_2 } \right)^2 + \left( {y_1-y_2 } \right)^2 } \]
\[d = \sqrt {\left( {2 + 1 } \right)^2 + \left( {-3 + 2 } \right)^2 }\]
\[d = \sqrt {\left( {3 } \right)^2 + \left( {1 } \right)^2 }\]
\[d = \sqrt {9 + 1 }\]
\[d = \sqrt {10}\]
Example 3
Find the length of a line segment whose endpoints are (3, –3) and (–1, –4).
Solution
Given that:
The coordinates are (3, –3) and (–1, –3)
Again, we have to find the segment’s length. We know that the distance formula is:
\[ d = \sqrt {\left( {x_1-x_2 } \right)^2 + \left( {y_1-y_2 } \right)^2 } \]
\[ d = \sqrt {\left( {3 + 1 } \right)^2 + \left( {-3 + 4 } \right)^2 } \]
\[ d = \sqrt {\left( {4 } \right)^2 + \left( {1 } \right)^2 } \]
\[ d = \sqrt {16 + 1 } \]
\[ d = \sqrt {17} \]
All mathematical drawings and images were created with GeoGebra.
