Quotient|Definition & Meaning

Division is, as we know, the fundamental operation in mathematics. Whenever we divide a number by another, the resulting number is called a quotient. For example, if we divide the number 100 by the number 10, we will get 10 as a result. This number 10 that results from the division operation is called the quotient. 

The following figure describes this process:

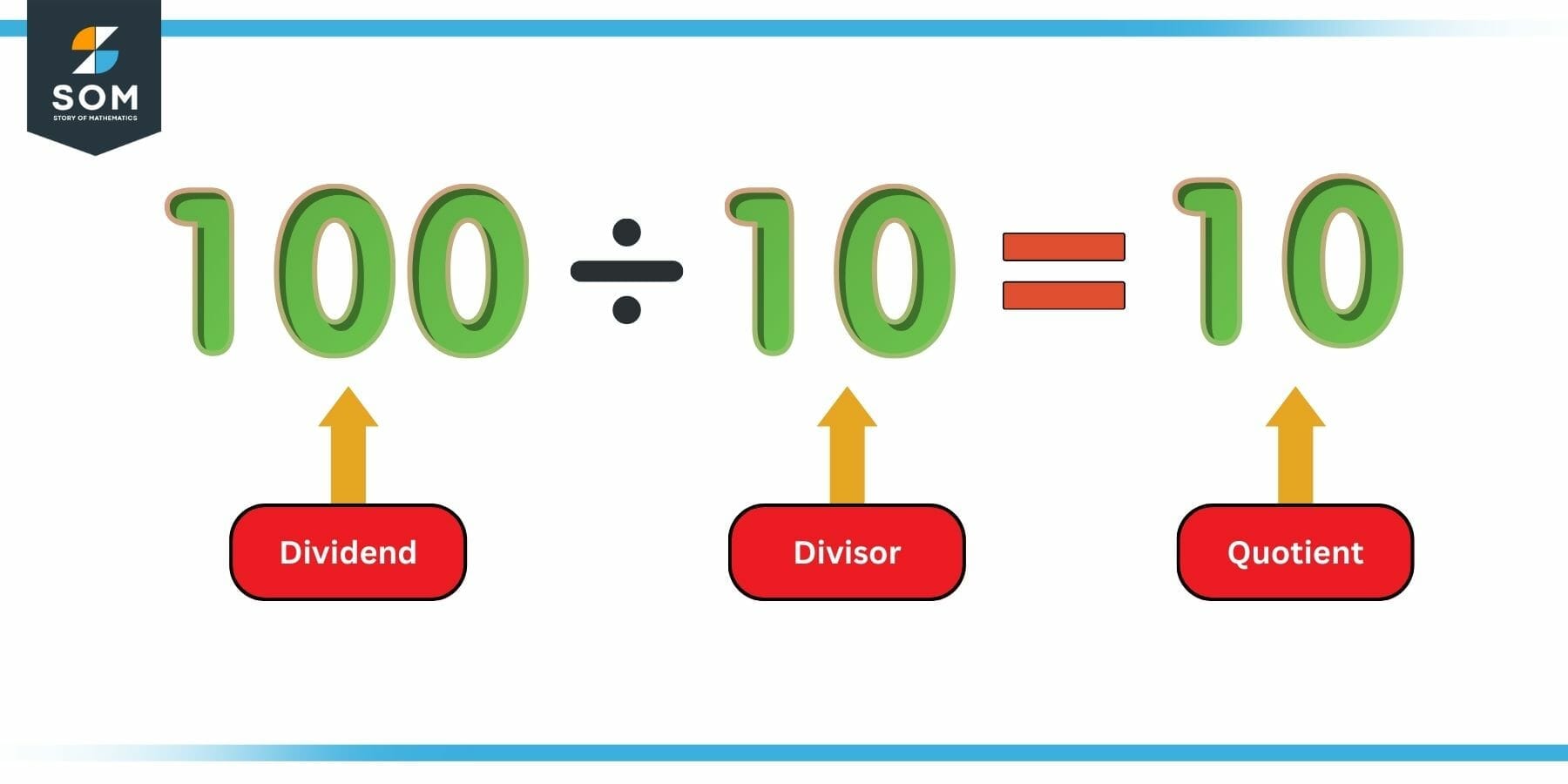
Figure 1: Example of Quotient

As the diagram shows, the number that is being divided is called the dividend, while the number that is dividing the other (dividend) is called the divisor. For this example, 100 is the dividend, while 10 is the divisor.

Explanation of Quotient

Quotient is a mathematical term used to describe the result of division. It refers to the number of times one quantity is contained within another. In other words, it is the result of dividing one number by another. Division is the process of finding how many times one number is contained within another, and the quotient is the answer to that division problem.

The following diagram illustrates this concept:

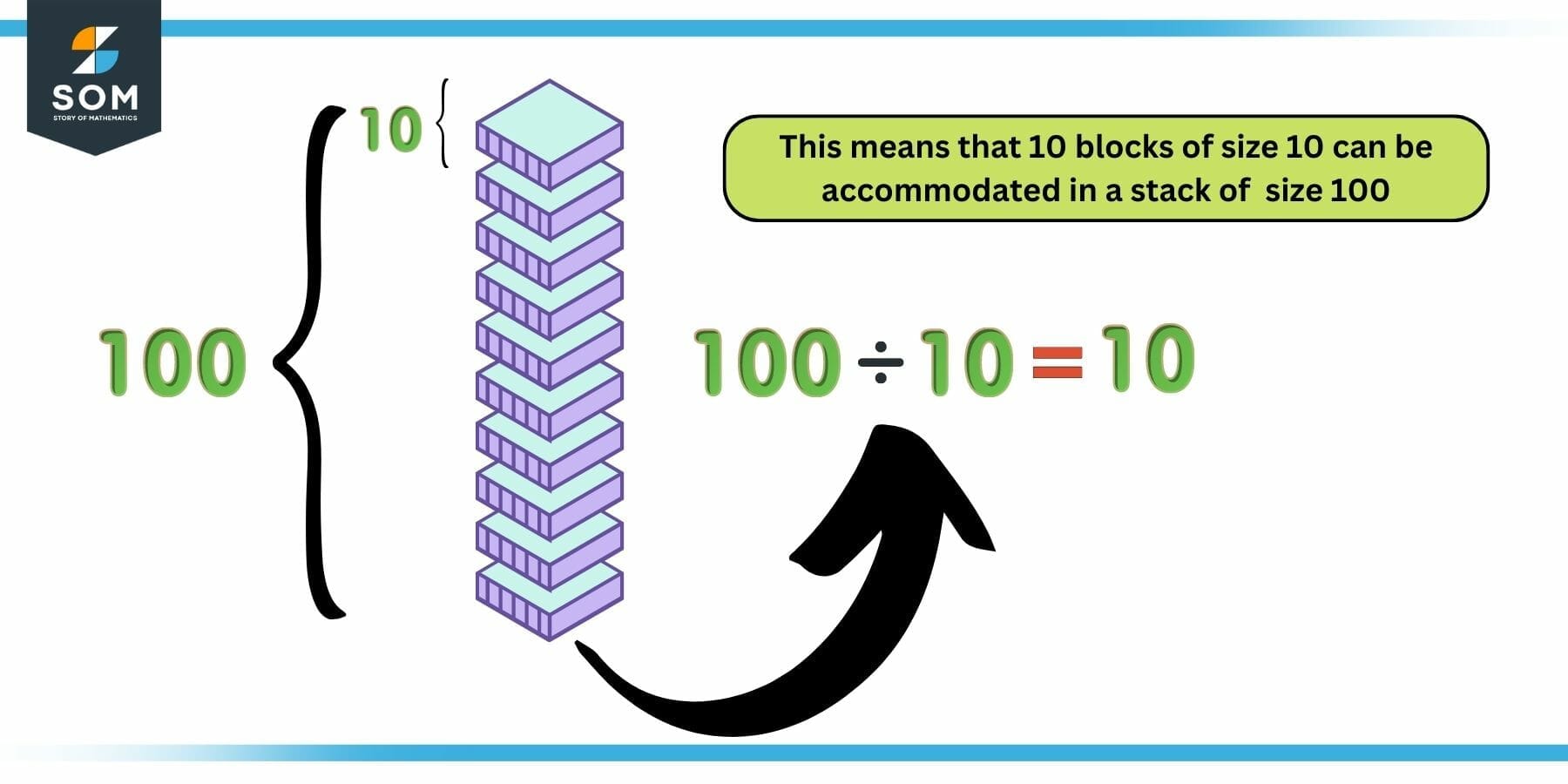
Figure 2: Illustration of Division

In mathematics, the division is represented by the symbols ÷ or /. When we divide two numbers, we place the dividend (the number being divided) over the divisor (the number by which we are dividing) and use the ÷ symbol to indicate the division operation. For example, if we want to divide 12 by 4, we write the equation as 12 ÷ 4 = 3, where 3 is the quotient.

It is also important to note that a quotient is always a real number, meaning it can be either a whole number or a fraction. For example, if we divide 12 by 3, the quotient is 4, which is a whole number. On the other hand, if we divide 18 by 5, the quotient is 3.6, which is a fraction.

Significance of Quotient

Overall, the importance of quotient lies in the versatility and utility of division operation. It is a fundamental concept that is used in a wide range of mathematical, scientific, and real-world applications and helps individuals to better understand and solve mathematical problems. 

The quotient is an important mathematical concept that has many real-world applications. It is used to find the result of division and is essential for solving many mathematical problems and for understanding advanced mathematical concepts.

Understanding the concept of the quotient is a fundamental part of mathematical education and is essential for success in higher-level mathematics.

Applications of Quotient

Division and quotient are fundamental concepts in mathematics and are widely used in everyday life.

For example, when we purchase items at a store, we use the concept of quotient to determine how many of a certain item we can purchase with a specific amount of money. When we split a pizza into equal pieces, we use the quotient to determine how many pieces each person will receive.

The quotient has many real-world applications in various fields, including:

1. Finance: In finance, quotients are used to calculate interest rates, loan payments, and investment returns.
2. Business: In business, quotients are used to calculate profits, losses, and market shares.
3. Engineering: In engineering, quotients are used to calculate ratios, proportions, and scaling factors.
4. Science: In science, quotients are used to calculate rates of change, such as velocity, acceleration, and growth rates.
5. Cooking: In cooking, quotients are used to determine the proportions of ingredients needed to make a specific quantity of a dish.
6. Sports: In sports, quotients are used to calculate averages, such as batting averages and scoring averages.
7. Surveying: In surveying, quotients are used to calculate distances, angles, and elevations.
8. Education: In education, quotients are used to calculate grades, class sizes, and student-teacher ratios.

Figure 3: Applications of Quotient

Examples of Quotient

In addition to its use in everyday life, the concept of quotient also plays an important role in advanced mathematical concepts such as fractions, decimals, and ratios. Understanding the concept of the quotient is essential for solving many mathematical problems and for understanding more advanced mathematical concepts.

Following are some of the examples of quotients that we come across in mathematics very often.

Percentage

Percentage is a very common term used in many areas of life. We have all heard of it and even used it in some way or another. A percentage is nothing but a quotient of some given value and the total value multiplied by 100. Suppose you want to find the percentage of your marks (say a) out of total marks (say b) in a certain exam.

The formula for such a calculation is as follows:

Marks Percentage = (Y / X) x 100 %

Interest Rate

Suppose you borrowed some amount X from a Bank, and at the end of the year, you must return an amount Y to settle the loan. Interest rate is defined as 100 times the quotient of Y and X:

Interest Rate = (Y / X) x 100 %

Return on Investment (ROI)

Suppose you invested some amount X on a business, and at the end of the year, you sell out the business and liquidate all your asset for an amount of Y in return. Your return on investment (ROI) is defined as 100 times the quotient of Y and X:

Return on Investment (ROI) = (Y / X) x 100 %

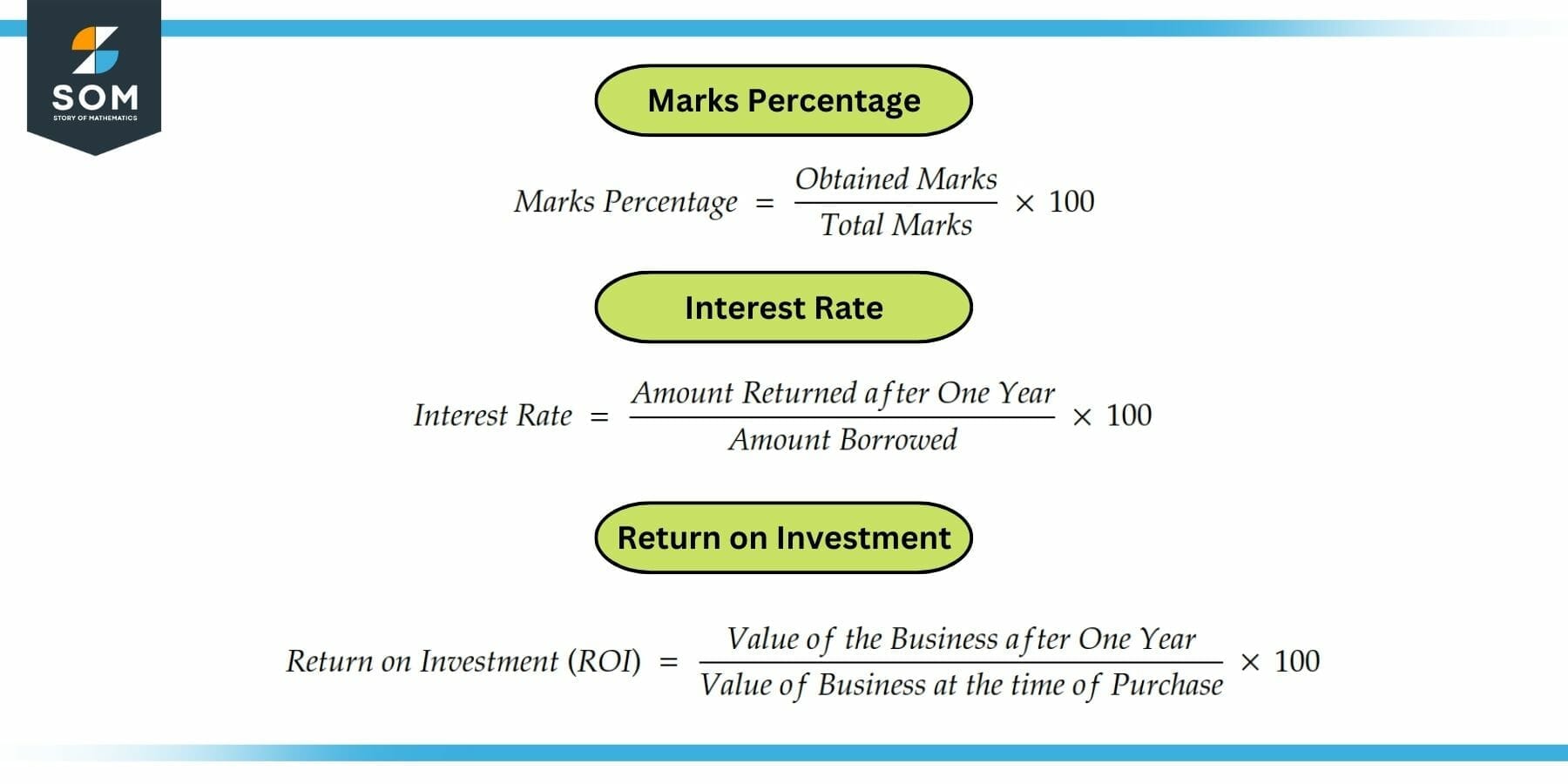
Figure 4: Some Important Quotients

Numerical Problems Involving Quotients

Example 1

You invested 1000 dollars in a certain stock. After a year, you sold the stock for 1200 dollars. What was the return on investment in percentage?

Solution

Here:

Invested Amount = X = 1000 dollars

Returned Amount = Y = 1200 dollars

So:

Return on Investment (ROI) = (Y / X) x 100 %

Return on Investment (ROI) = (1200 / 1000) x 100 %

Return on Investment (ROI) = 120 %

Example 2

A certain bank offers loans at the interest rate of 10 percent. How much amount would you have to return to the bank after one year if you borrowed 10,000 dollars?

Solution

Here:

Borrowed Amount = X = 10,000 dollars

Interest Rate = 10 %

So if Y is the interest amount:

Interest Rate = (Y / X) x 100 %

10 % = (Y / 10,000) x 100 %

Interest Amount = Y = 1,000 dollars

Amount to return = X + Y = 10,000 + 1,000

Amount to return = 11,000 dollars

Example 3

Suppose you took a mathematics course in your college and received 110 marks out of 120. What percentage did you receive?

Solution

Here:

Marks Obtained = a = 110

Total Marks = b = 120

So:

Marks Percentage = (a / b) x 100 %

Marks Percentage = (110 / 120) x 100 %

Marks Percentage = 91.67 %

All images were created with GeoGebra.

Quintillion Definition < Glossary Index > Radian Definition