JUMP TO TOPIC
- Definition
- Formula To Calculate the Percent
- What Is the Formula for Calculating the Percent of a Number
- Percent Difference
- The Formula for Calculating Percent Differences
- Increases and Decreases in Percents
- How To Convert Fractions to Percents
- Marks Percent
- Percentage vs. Percent
- Solved Examples for Finding the Percentage
Percent|Definition & Meaning
Definition
The percent is a fraction out of a hundred. It represents or expresses an amount in the fraction of a hundred. This can be calculated by dividing the part of the whole number or amount by the total number and then multiplying by 100.
Per means each, and cent means hundred, so it shows an amount for each hundred. The symbol used to represent percent is “%”. As the percent is a ratio of two similar types of numbers, it has no scientific dimensions called dimensionless numbers.

The percent can also be expressed in decimal or fraction form, such as 0.9%, and 0.12%. When it comes to academics, the grades obtained in any subject are calculated in terms of percent. For example, Alina achieved 80% marks in his final exams. This percent is calculated as the sum of Alina’s total marks in all subjects to the total marks.
Formula To Calculate the Percent
The percent is calculated by dividing the given value by the total value and multiplying the result by 100.
Percent = (given value/total value) × 100
For example, Aslam has 10 chocolates. Out of these, he gave 5 chocolates to his brother. Calculate the percentage of the remaining chocolates.
Percentage = 5 / 10 × 100 = 50%
So, the percent of remaining chocolates = 50%
What Is the Formula for Calculating the Percent of a Number
Percent (%) of Number = X
In this case, X represents the percent required.
When the % sign is removed, the above formula can be expressed as follows
P/100 x Number = X
For example, calculate 40% of 50. Let:
40% of 50 = X
40/100×50 = X
X = 20
Percent Difference
It is a measure of the change in a quantity’s value over time expressed in percent. There are some situations in which we need to know if some quantity has increased or decreased as a percent, which is also known as a percent change in the quantity. For example, an increase in poverty, and a decrease in forests.
The Formula for Calculating Percent Differences
The formula below can be used if two values are given and you want to find the percent difference between them.
Percent difference = (x-y) / ({x+y} / 2) × 100
For example, if 50 and 60 are two different values, the percent difference between 50 and 60 can be found by
Percent difference between 50 and 60= (50-60) / ({50+60} / 2) × 100
Increases and Decreases in Percents
Two cases may arise when calculating percent differences, the percent either increases or decreases. A percent increase is calculated by subtracting the original number from the new number, dividing the result by the original number, and multiplying the result by 100. Let us suppose the new number=V1, whereas the original number is equal to=V2 then the percent increase can be calculated by using the formula mentioned below:
Percent (%) increase = [(V1 – V2) / V2] × 100
So, increase in number= V1-V2 (where V1 and V2 represent the new number and the original number)
Accordingly, a percent decrease can also be calculated by subtracting the original number from the new number, dividing the new number by the original number, and multiplying the result by 100. Let us suppose the new number=V1, whereas the original number is equal to = V2, then the percent decrease can be calculated by using the formula mentioned below:
Percent (%) decrease = [(V2 – V1) / V2] × 100
So, decrease in number= V2 – V1 where V1 and V2 represent the original and new number). Therefore, if the answer is negative, then there is a decrease in the percentage of the answer.
How To Convert Fractions to Percents
You can represent a fraction as x/y.
Taking the fraction and multiplying and dividing it by 100, we get the following:
x/y × 100/100 = (x/y × 100) × 1/100……(i)
According to the definition of percent, we can say that 1/100 = 1 percent (%). Equation (i) can therefore be written as follows:
(x/y) × 100%
Hence, by multiplying a fraction by 100, it is possible to convert it to a percent.
There is an interrelationship between fractions, ratios, percent, and decimals. To better understand how to convert one form into another, let’s look at the following table.
| Serial no | Ratio | Fraction | Percent | Decimal |
| 1 | 1:20 | 1/20 | 5 | 0.05 |
| 2 | 2:10 | 2/20 | 10 | 0.1 |
| 3 | 5:15 | 5/15 | 33 | 0.33 |
| 4 | 7:2 | 7/2 | 350 | 3.5 |
| 5 | 6:10 | 6/10 | 60 | 0.6 |
Marks Percent
In exams, students are given marks out of 100. In calculating the marks, the percent is used. In the case of a student who scored out of total marks, then the scored marks are to be divided by the total marks and multiplied by 100.
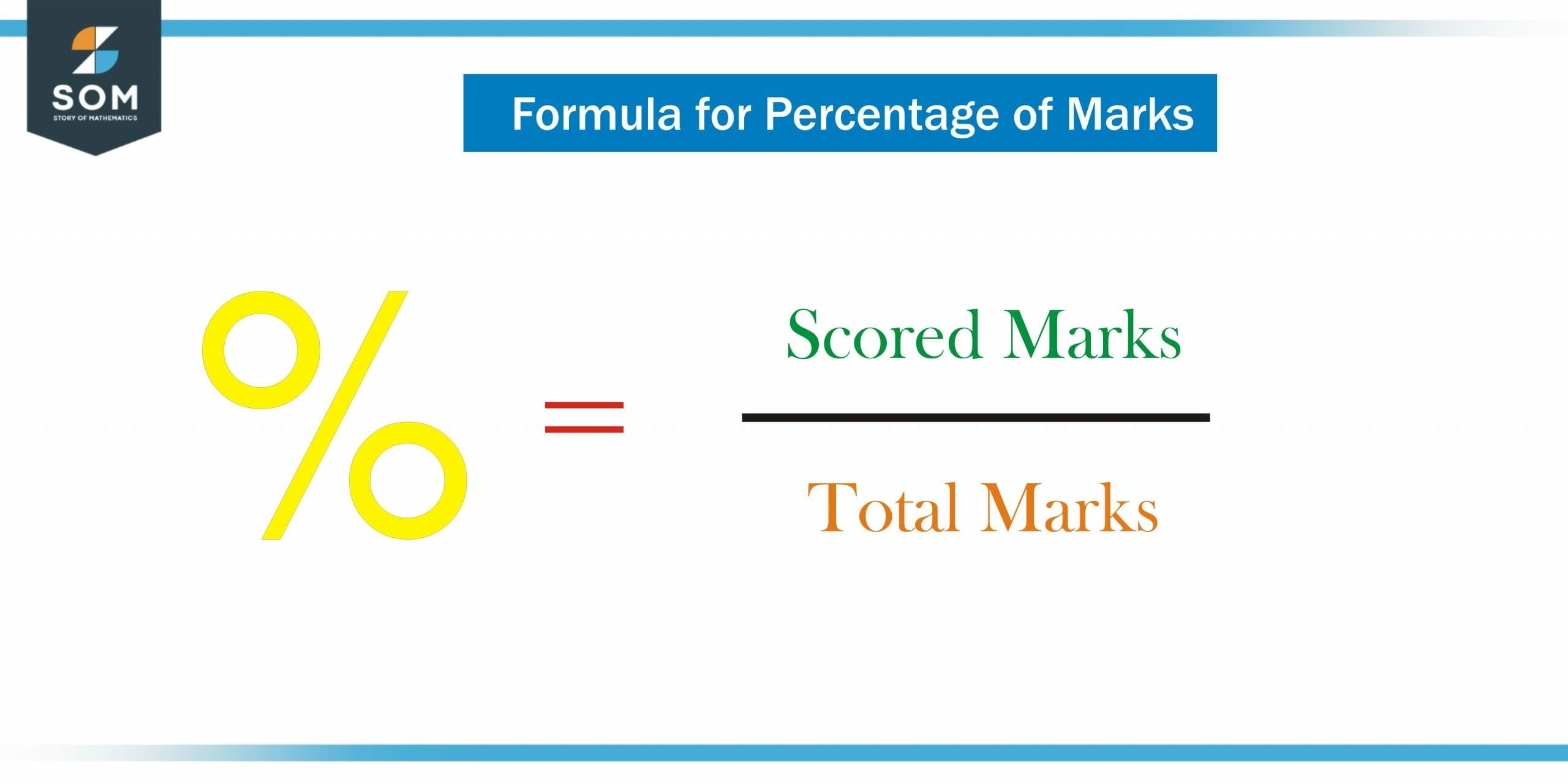
Figure 2 – Formula for calculating the Percentage of obtained marks
Here are a few examples.
| Subjects | Marks obtained | Total marks | Percentage |
| English | 40 | 75 | 53% |
| Maths | 55 | 75 | 73% |
| Urdu | 70 | 100 | 70% |
| Science | 89 | 100 | 89% |
| Pak study | 48 | 50 | 96% |
Percentage vs. Percent
There is a close relationship between percentage and percent.
| Percent | Percentage |
| The percent symbol (%) is always followed by a number. | A percent is expressed without using a number in its representation. |
| For example, the percentage of participants who were abjured was more than 75%. | For example, The percentage of students who failed exams is between 30 to 40%. |
Solved Examples for Finding the Percentage
Example 1
If 10% of 50% of a number is 10, then what is the number?
Solution
Suppose the required number is X. As we know that:
10%=10/100 and 50% = 50/100
(10/100) × (50/100) × X = 10
(10×100×100)/ (50×10)
100,000/500
X = 200
Example 2
a. 1/4 is what percent of2/15?
Solution
Suppose X% of 1/4 is 2/15:
(1/4×100) × X = 2/15
X (2/15) × 4 × 100
53%
b. Find out the number which is 20% less than 60.
Solution
Let the required number = X, then:
X = 20% of 60
20/100×60
20×60/100
X = 12
Example 3
What is the value of the sum of (14%) of 4.2, and (12%) of 4.2)?
Solution
Let the unknown value = X:
X = 14% 4.2+ 12% 4.2
(4.2×14)/100 + ( 4.2×12)/100
0.588 + 0.504
1.092
Example 4: Real-life Problem
In a grocery shop, a shopkeeper has some bananas. He sells 60% bananas and still has 120 bananas. How many bananas did he originally have?

Figure 3 – Bananas in a Shop
Solution
Suppose X = number of bananas he had originally. Based on the question given, we have:
(100-60)% of X = 120
40/100 of X = 120
X = 120 × 100 / 40 = 300
All the mathematical images are generated using GeoGebra.
