Pentagonal Numbers|Definition & Meaning

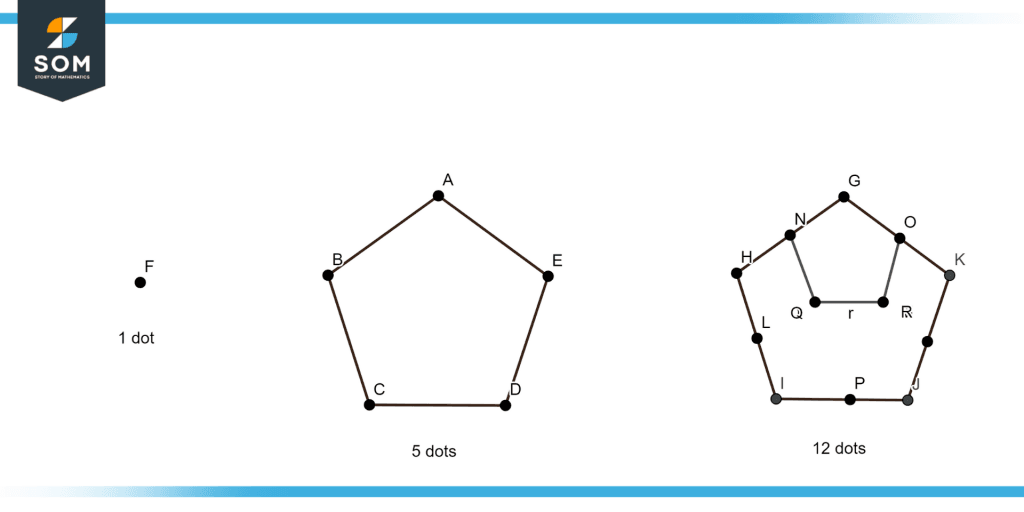
Figure 1 – Pentagonal Numbers 

Figure 1 illustrates the graphical view of three pentagonal numbers.

Like square and triangle numbers, pentagonal numbers are figurate numbers. A figurate number is one that may be represented by a regular geometric pattern that is often made up of evenly spaced dots.

A pentagon is the shape of a pentagonal number. In contrast to square and triangular numbers, patterns created by pentagonal numbers are not rotationally symmetrical.

Given that n dots make up each side of a pentagon and that the pentagons are layered so that they share a vertex, a pentagonal number denotes the total number of different dots that make up a pentagon.

For instance, the third pentagonal number in figure 1 above includes 12 different dots overall and 3 dots on each side.

Generalized Pentagonal Numbers

The generalized pentagonal numbers can be found by using the formula

P_n=$\mathsf{\dfrac{3n^2-n}{2}}$

Determination of the Number To Be Pentagonal

In order to check whether the number is pentagonal or not, we have the following formula

N = $\mathsf{\dfrac{\sqrt{24x + 1}+1}{6}}$

If after putting the given number x in the formula, N is a natural number then we can say that the given number x is a pentagonal number.

Relationship Between the Pentagonal Numbers and Integers

The sum of the n integers starting at n forms the nth pentagonal number (i.e. from n to 2n-1). Additionally, the following connections exist:

P_n = P_n + 3n – 2 = 2P_n – P_n-2 + 3

Relationship Between the Pentagonal Numbers and Triangular Numbers

Triangular numbers and pentagonal numbers have a close relationship. The (3n -1)th triangular number is one-third of the nth pentagonal number. Furthermore, T_n is the nth triangular number:

P_n = T_n + n² = T_n  + 2T_n = T_2n-1 – T_n

Uses of Pentagonal Numbers

According to Euler’s pentagonal number theorem, generalized pentagonal numbers are crucial to his theory of partitions.

Some Examples of Pentagonal Numbers

Example 1

a) Give the graphical view of the pentagonal number 5 using the pentagon.

b) Give the graphical view of the pentagonal number 12 using the pentagon.

Solution

a) In order to draw the pentagonal number five we have to draw the pentagon having five distinct dots as illustrated in figure 2

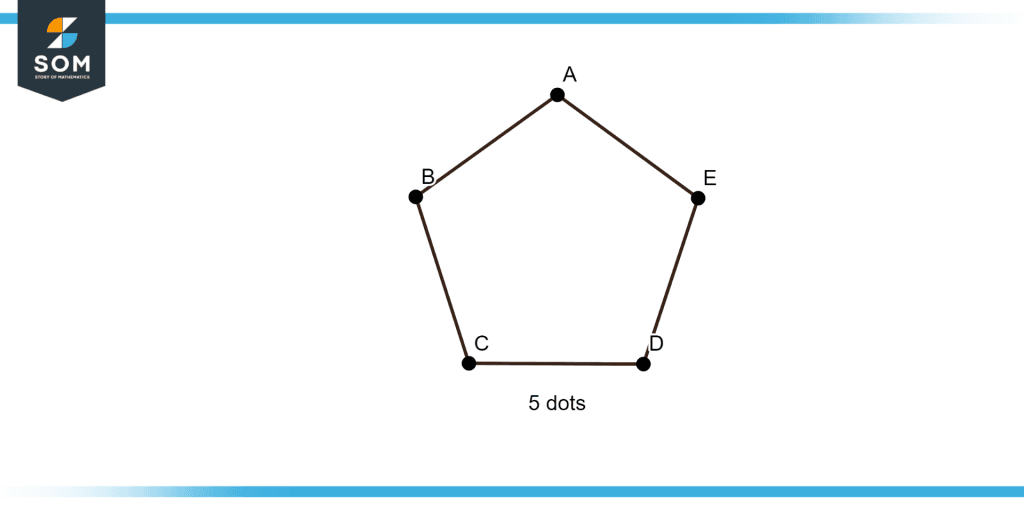
Figure 2 – Graphical view of the pentagonal number five

b) In order to draw the pentagonal number twelve, we have to draw the pentagon having twelve distinct dots, as illustrated in figure 3.

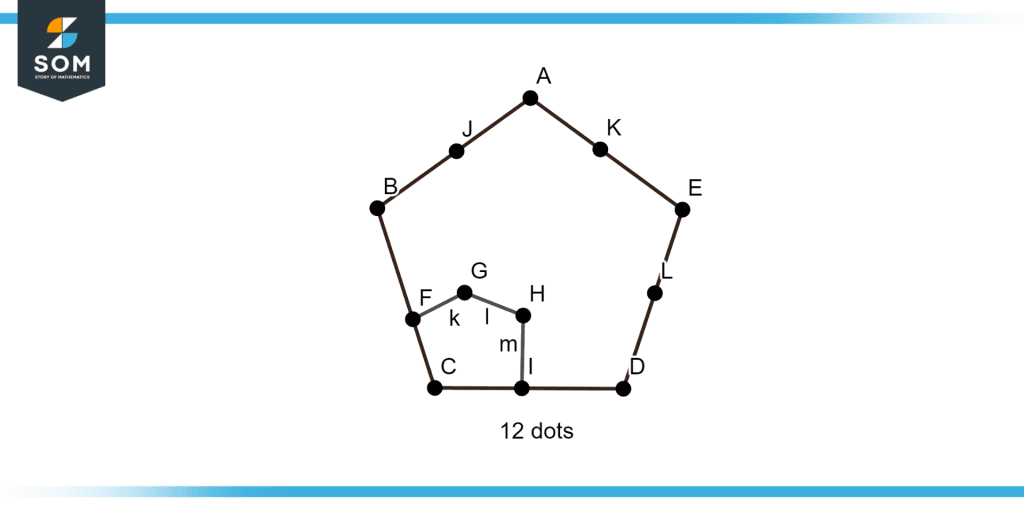
Figure 3 – Graphical view of the pentagonal Number Twelve

Example 2

Find the pentagonal number for the following n

a) 12

b) 14

c) 5

d) 30

e) 2

f) 10

Solution

a) As we know, the formula to find the pentagonal numbers:

P_n = $\mathsf{\dfrac{3 n^2 -n}{2}}$

We have to put the value of n into the formula in order to get the corresponding pentagonal number, if n is equal to 12 so:

P₁₂ = $\mathsf{\dfrac{3 (12)^2 -12}{2}}$

P₁₂ = $\mathsf{\dfrac{3 (144) -12}{2}}$

P₁₂ = $\mathsf{\dfrac{432 -12}{2}}$

P₁₂ = $\mathsf{\dfrac{420}{2}}$

P₁₂ = 210

b) if n is equal to 14 so:

P₁₄ = $\mathsf{\dfrac{3 (14)^2 -14}{2}}$

P₁₄ = $\mathsf{\dfrac{3 (196) -14}{2}}$

P₁₄ = $\mathsf{\dfrac{588 -14}{2}}$

P₁₄ = $\mathsf{\dfrac{574}{2}}$

P₁₄ = 287

c) As we know, the formula to find the pentagonal numbers:

P_n = $\mathsf{\dfrac{3 n^2 -n}{2}}$

We have to put the value of n into the formula in order to get the corresponding pentagonal number, if n is equal to 5 so:

P₅ = $\mathsf{\dfrac{3 (5)^2 -5}{2}}$

P₅ = $\mathsf{\dfrac{3 (25) -5}{2}}$

P₅ = $\mathsf{\dfrac{75 -5}{2}}$

P₅ = $\mathsf{\dfrac{70}{2}}$

P₅ = 35

d) if n is equal to 30 so:

P₃₀ = $\mathsf{\dfrac{3 (30)^2 -30}{2}}$

P₃₀ = $\mathsf{\dfrac{3 (900) -30}{2}}$

P₃₀ = $\mathsf{\dfrac{2700 -30}{2}}$

P₃₀ = $\mathsf{\dfrac{2670}{2}}$

P₃₀ = 1335

e) We have to put the value of n into the formula in order to get the corresponding pentagonal number. If n is equal to two, so:

P₂ = $\mathsf{\dfrac{3 (2)^2 -2}{2}}$

P₂ = $\mathsf{\dfrac{3 (4) -2}{2}}$

P₂ = $\mathsf{\dfrac{12 -2}{2}}$

P₂ = $\mathsf{\dfrac{10}{2}}$

P₂ = 5

f) if n is equal to 10, so:

P₁₀ = $\mathsf{\dfrac{3 (10)^2 -10}{2}}$

P₁₀ = $\mathsf{\dfrac{3 (100) -10}{2}}$

P₁₀ = $\mathsf{\dfrac{300 -10}{2}}$

P₁₀ = $\mathsf{\dfrac{290}{2}}$

P₁₀ = 145

Example 3

a) Check either 92 is a pentagonal number or not.

b) Check either 100 is a pentagonal number or not.

Solution

In order to evaluate whether the given number is pentagonal or not, we have the following formula

N = $\mathsf{\dfrac{\sqrt{24x + 1}+1}{6}}$

a) As we given the number x which is equal to 92 so we put it in the formula so

N = $\mathsf{\dfrac{\sqrt{24 (92) + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{2208 + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{2209}+1}{6}}$

N = $\mathsf{\dfrac{47+1}{6}}$

N = $\mathsf{\dfrac{48}{6}}$

N = 8

N is equal to eight, which is a natural number so the given number x is indeed a pentagonal number.

b) As we were given the number x, which is equal to 100 so we put it in the formula so:

N = $\mathsf{\dfrac{\sqrt{24 (100) + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{2400 + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{2401}+1}{6}}$

N = $\mathsf{\dfrac{49+1}{6}}$

N = $\mathsf{\dfrac{50}{6}}$

N = 8.33

N is equal to 8.33, which is not a natural number, so the given number x is not a pentagonal number.

Example 4

Check whether the following numbers are pentagonal or not.

a) 5

b) 23

Solution

In order to evaluate whether the given number is pentagonal or not, we have the following formula:

N = $\mathsf{\dfrac{\sqrt{24x + 1}+1}{6}}$

As we were given the number x, which is equal to 5 so we put it in the formula so:

N = $\mathsf{\dfrac{\sqrt{24 (5) + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{120 + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{121}+1}{6}}$

N = $\mathsf{\dfrac{11+1}{6}}$

N = $\mathsf{\dfrac{12}{6}}$

N = 2

N is equal to two, which is a natural number, so the given number x is a pentagonal number.

the number x, which is equal to 23, so we put it in the formula:

N = $\mathsf{\dfrac{\sqrt{24 (23) + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{552 + 1}+1}{6}}$

N = $\mathsf{\dfrac{\sqrt{553}+1}{6}}$

N = $\mathsf{\dfrac{23.5+1}{6}}$

N = $\mathsf{\dfrac{24.5}{6}}$

N = 4.08

N equals 4.08, which is not a natural number, so the given number x is not a pentagonal number.

All images were created using GeoGebra.

Pascals Triangle Definition < Glossary Index > Pentomino Definition