Parity|Definition & Meaning

Even numbers are to be counted by two’s in both directions from zero. For example, -4, -2, 0, 2, 4, 6, 8, … and odd numbers are to be counted by two’s in both directions from one. For example, -5, -3, -1, 1, 3, 5, 7, 9,… 

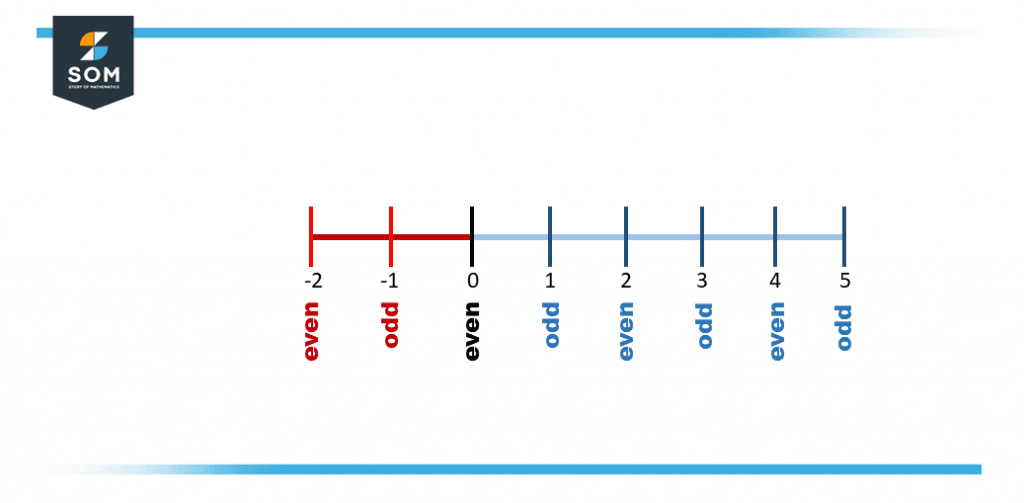
Figure 1 – Parity on Number Line

Even Numbers

An even number can be obtained if a number is a factor of 2. In order words, any number that is completely divisible by 2 with the reminder 0 is an even number. This can be easily understood with the assistance of an example.

Suppose John has 8 toffees. If he tries to put them in groups, he can pair all 8 toffees and form 4 pairs. There are no toffees that are left unpaired. Therefore, he can conclude that 8 is an even number.

Now, let us divide 8 by 2. We get the quotient as 4, which is the number of pairs that are formed. We get the remainder as 0, which should be equal to the number of toffees that are left unpaired.

Whenever Ali tries to pair an even number of toffees, he will be left with NO toffee that is unpaired. In different words, whenever we divide an even number by 2, the remainder we will always get is 0.

Even numbers will always end with the last digit as 0, 2, 4, 6, or 8. Some examples of even numbers, as explained above, are 12, 16, 20, 28, 40, 44, and 56. These are proved to be even numbers as these numbers are easily divisible by 2.

It should be noted that the smallest positive natural number that is even is 2. The formula for even numbers is = 2n, where n is an integer.

Odd Numbers

Those numbers which are not completely divisible by 2, which means they do not produce a remainder of 0, are known as odd numbers. If you intend to separate an odd number from the middle, it will not be separated into two integers evenly.

When an odd number is divided by 2, it will leave a remainder. Examples of odd numbers are 1, 5, 7, 9, etc. Odd numbers are the exact opposite concept of even numbers.  The simplest way to remember an odd number is ‘it is not divisible by 2’.

Figure 2 – Odd Number Example

Odd numbers in the form of 2k+1, where k is an integer, such numbers are odd numbers. It should be known that the numbers or sets of integers can either be odd or even on a number line. If these numbers are divided by 2, a remainder will be left. In the number line, the first positive odd number is 1.

Parity of Even and Odd Numbers

Even and odd numbers are from opposite parties, e.g., 42 (even number) and 27 (odd number) are from opposite parties. Certainly, the parity of the number zero is even. Any two consecutive integers will have opposite parities.

An integer number written in the decimal numeral system is either even or odd depending on whether the last digit is even or odd. That is, when the last digit is any of the following: 1, 3, 5, 7, or 9, then it is odd; if not, it is even—as the last digit of an even number is from the following: 0, 2, 4, 6, or 8.

The same thing will happen when using any even base. In certain, a number represented in the binary numeral system will be odd if the last digit is 1; and it will be even if the last digit is 0. In an odd base, the number will be even depending on the sum of its digits, it is even if and only if the sum of its digits is even.

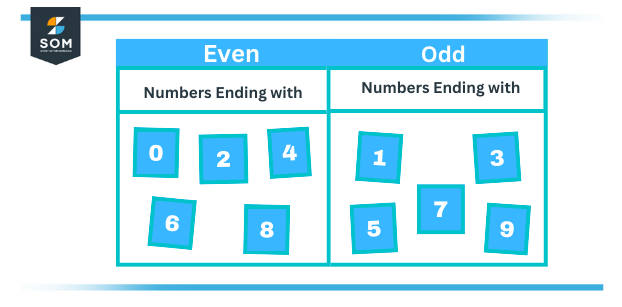
Figure 3 – Even and Odd Parity

How Can We Check if a Given Number Is either Even or Odd?

To find out if any number is odd or even, you will need to check the number in one’s (or unit’s) place. That certain number in one’s place will actually identify the number as odd or even.

• Even numbers will end with 0, 2, 4, 6, 8
• Odd numbers will end with 1, 3, 5, 7, 9

This is the most simple trick to identify whether the numbers are even or odd. Let’s take the numbers 1, 373, and 627, which end with an odd number, i.e., 1, 3, and 7. Thus, the given numbers 1, 373, and 627 are odd numbers. Therefore, the numbers are not even numbers. In that way, 4 and 146 are even numbers since they end with 4 and 6.

Some Properties of Parity

Property 1: The Sum of Two Even Numbers Is Even

Let x and y be two chosen even numbers such that x and y can be represented as follows,

x = 2j and y = 2k

where j and k are integers.

Taking the sum of x and y:

x + t = 2j + 2k

Since on the right-hand side, both terms are multiples of 2, we can rewrite the statement:

x + y = 2(j + k)

Since both j and k are integers, so their sum will also be an integer. Let m= j+k, where m is an integer. Putting m into the equation:

x + y = 2m

Since the sum of x and y is in an even number, we conclude that the sum of any two given even numbers is an even number as proved.

Property 2: The Sum of Two Odd Numbers Is Even

Following the same practice as above to prove that an even number is obtained if two odd numbers are summed up, but using the definitions of odd in place of even.

Let x and y be two chosen odd numbers such that x and y are represented as,

x = 2j + 1 and y = 2k +1

where j and k are integers.

Take the sum of x and y:

x + y = 2j + 1 + 2k +1

Which simplifies to:

x + y = 2j + 2k +2

Since all on the right-hand side, the terms are all multiples of 2, rewrite the above statement as follows:

x + t = 2(j + k + 1)

Since they are all integers, so their sum will also be an integer. Therefore, make the replacement: j + k + 1 = m, where m is an integer.

x + y = 2m

Since the sum of x and y comes out to be an even number, we can say that if two odd numbers are added, we get an even number.

Property 3: Sum of an Even and Odd Number Is Odd

Let two odd numbers, x and y, such that:

x = 2j and y = 2k +1

where j and k are integers.

Sum x and y:

x + y = 2j+ 2k+ 1

Grouping and factorizing:

x + y = 2(j + k) + 1

Since j and k are said to be integers, the sum of j and k is also an integer. Make the replacement: m = j + k, where m is an integer.

x + y = 2(m) + 1

Since the sum of x and y results in an odd number, the aggregate of a given even and odd number is an odd number, as proved.

Property 4: Product of Two Even Numbers Is Even

Let x and y be two chosen even numbers such that:

x = 2j and y = 2k

where j and k are integers.

Take the product of x and y.

xy = 2(j)(k)

Using commutativity property, rewriting the product:

xy = 2(2jk)

Since both right-handed variables are integers, their product will also be an integer. Make the replacement: m = 2jk, where m is an integer:

xy = 2m

Hence proved that the product of two even integers is even.

Parity Solving Example

Example

What will be the parity if we add the first and last even numbers between 10 and 60?

Solution

The first even number between 10 and 60 is 12.

The last even number between 10 and 60 is 58.

Sum = 12 + 58 = 70

70 is even, so it is even parity.

All images/mathematical drawings were created with GeoGebra.

Parentheses Definition < Glossary Index > Pascals Triangle Definition