JUMP TO TOPIC
Parentheses|Definition & Meaning
Definition
In mathematics, parentheses ( ) are used to enclose numbers or variables that are part of a mathematical expression. They can be used to indicate the order in which operations should be performed, or to group terms.
It is common for math problems to contain a greater number of symbols and expressions as the level of difficulty in the problem increases. Some symbols are easy to recognize in the beginning, such as the main operation sign, equals sign, and greater than and less than symbols. It is important to keep in mind that parentheses should not be confused with either braces or brackets.
Figure 1 – Symbol of Parentheses
Parentheses and Order of Operation
There is a concept called the order of operations that is accompanied by parentheses that indicates that whatever is in the parenthesis must be solved first when it comes to the order of operations.
When multiple operations are part of a single problem, the order of operations specifies which should be done first. People typically refer to it as PEMDAS, which stands for the pneumonic device.
Use of Parentheses in Maths
Parentheses can be used to separate numbers in math. Math problems sometimes contain negative numbers inside parentheses.
For example,
7 + (-9) = -2.
An operation involving a negative number is done first, just like a separate problem, since it is part of the operation. When the number is negative by itself, it will be written that way so as not to confuse the minus sign with the negative sign.
- Without parentheses 12 – – 6 = 18
- With parentheses 12 – (-6) = 18
The negative number is more obvious when it is present within parentheses. Whenever this occurs, we have to solve the problem using PEMDAS, and we have to pretend that the equation in the parentheses has already been solved. The following example shows a parenthesis problem with negative numbers.
20 + (-3 × 4 + 6)
| Steps | Operation | Results | Explanation |
| 1 | -3 × 4 = -12 | 20 + (-12 + 6) = | The first is to multiply the equation inside the parentheses. i.e., -3×4=-12 |
| 2 | -12 + 6 = -6 | 20 + (-6) = | Consider the negative -12 as part of the addition problem. |
| 3 | 20 + (-6) =14 | 16 | The number is still negative, so you can leave the parentheses out of the equation and solve it. |
The parentheses are often used to prevent confusion when two negative numbers are multiplied by one another. In such a case, the problem will look like this (-6) (-8).
Use of Parentheses for Multiplication
In math, parentheses are used for multiplying numbers. Parentheses indicate that you have to multiply an equation if there is no arithmetic operation. To better understand this, let’s take a look at an example
3 (2 + 2) = 3 × 4 = 12
To show two parentheses being multiplied, there are two possible ways to do so. There are two options to separate the two parentheses: either by placing a multiplication symbol between them or by placing them directly next to one another. Consider the following example (9/3) (12-9)
| Step | Operation | Result | Explanation |
| 1 | 9/3 = 3 | 3(12 – 9) = | In this case, since there are two sets of parentheses, we should start with the left parenthesis. |
| 2 | 12 – 9 = 3 | 3 × 3= | Once the operations within the parentheses have been completed, the parentheses can be removed |
| 3 | 3 × 3 = 9 | 9 | Once both operations are completed, we can multiply the results. |
Figure 2 – Some basic uses of Parentheses
Use of Parentheses in Different Mathematical Terms
- In math, parentheses are used to group numbers and specify how operations are performed.
- Parentheses can be used to enclose a function’s variables in the form, such as f(x), so that the values of the function will depend on the values of its parameters.
- A binomial coefficient is denoted by large parentheses around two numbers.
- In a set of two or more numbers, such as (a, b, c), parentheses around them are meant to indicate that there is an n-tuple of numbers connected in some kind of special way.
- The greatest common divisor can also be indicated by using parentheses.
For example, (6, 22) GCD of 6 and 22 is 2.
The Order of Operations
The order of operations is changed by parentheses.
When there are multiple symbols in an equation, follow this order
- Parentheses
- Exponents
- Multiplication/division (left to right)
- Addition/subtraction (left to right)
You should look at the terms present in the parentheses of an equation before you begin to attempt to solve it.
To better understand this, let us take a look at an example.
8 – 12 ÷ 4 – 2 × 1 + 6
We can solve this by applying the order of operations we learned earlier.
= 8 – 12 ÷ 4 – 2 × 1 + 6
= 8 – 3 – 2 × 1 + 6 (The first step is to divide)
= 8 – 3 – 2 + 6 (The second step is to multiply)
= 5 – 2 + 6(The third step is to subtract)
= 3 + 6 (again subtract)
= 9 (The fourth step is the addition)
Have you noticed? Due to the presence of parentheses in the equation, the answer to the same equation changed.
You should solve the inner expression of a parenthesis first if there are parentheses inside parentheses.
Here is an example that will help us better understand this
Simplify the following expression (3 + (5 × 4))
The inner bracket will be solved first, so the expression becomes 3 + 20 = 23.
Solved Examples
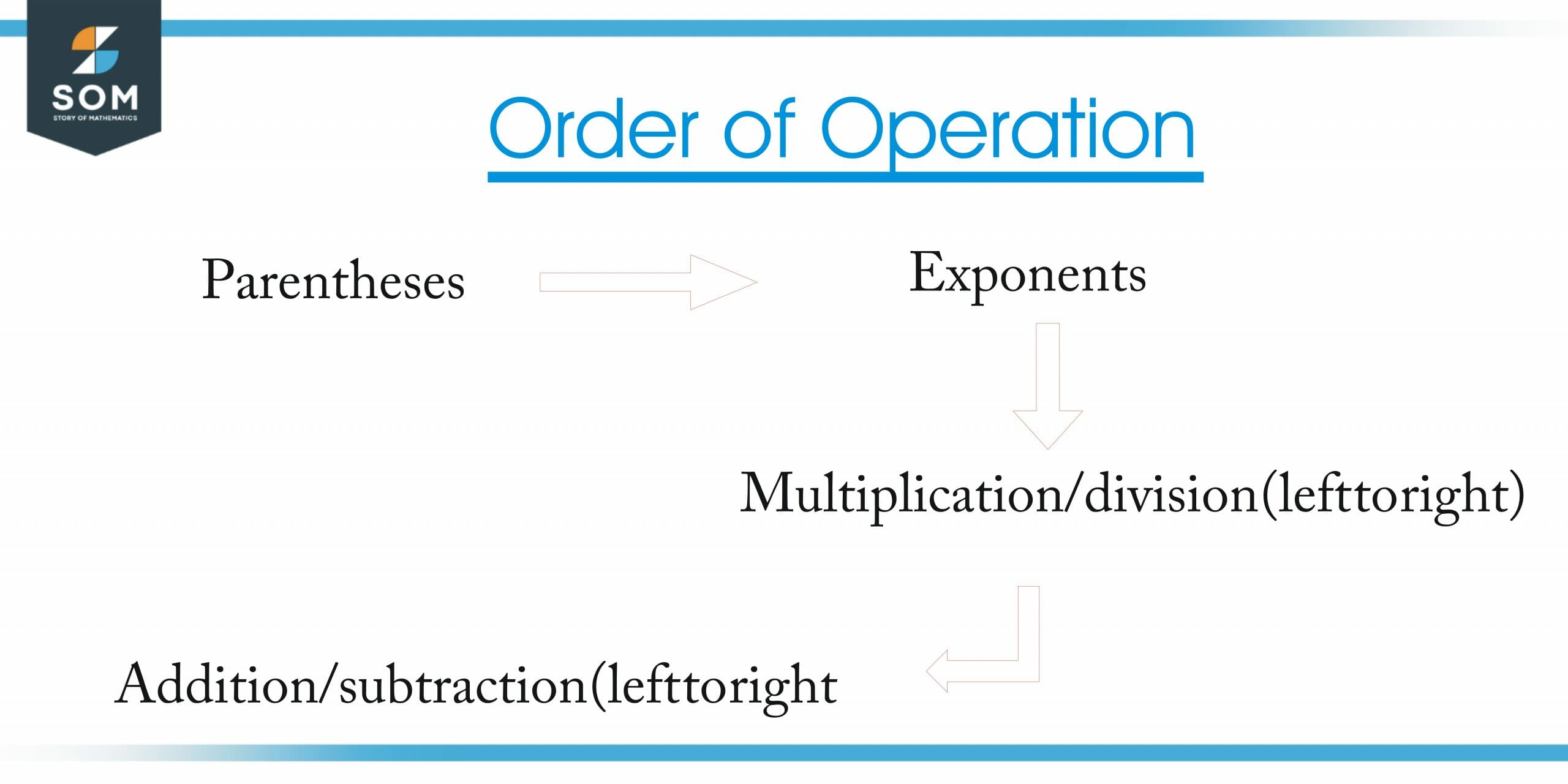
Figure 3 – Steps to solving problems
Example 1
Simplify the following expression: (4 + 6 × 8) – 6 + (3 × 4)
Solution
Solve the expressions within the parentheses first.
= (4 + 48) – 6 + 12 (multiply the numbers inside the parentheses)
= 52 – 6 +12 (solve the terms that are present inside the parentheses)
= 46 + 12 (there are no more parentheses; subtract 6 from 52)
= 58 (add the two terms together)
Example 2
Simplify the following expression: (3 × (8 – 6)) – ((8 ÷ 4) + 2)
Solution
Innermost parentheses are solved first, so we perform 8 – 6 and 8 ÷ 4, both of which result in 2:
= (3 × 2) – (2 + 2)
= 6 – 4 (solve the parentheses terms)
= 2 (subtract the resulting terms at the end)
Example 3
Simplify the following expression: 3(4 + 6) + 9(3 – 1)
Solution
First of all, we will solve the expression that is present inside the parenthesis
It is important to note that the parentheses also indicate a multiplication sign in this case. Whenever a number outside parentheses is written next to it without an operator on either the left or right side, it shows an implicit multiplication.
= 3 × 10 + 9 × 2 (solve terms inside parentheses and write out implicit multiplication with the results)
= 30 + 18 (solve multiplication first as per BODMAS)
= 48 (finally add the two terms)
Example 4
Solve the expression: 5(2 + 6) + 5(10 – 2)
Solution
First of all, we will solve the expression that is present inside the parenthesis
= 5(8) + 5(8)
= 40 + 40
= 80
All the mathematical images are generated using GeoGebra.


