JUMP TO TOPIC
Operation|Definition & Meaning
Definition
An operation is any mathematical process that takes a bunch of numbers as its input and produces an output. There is no mathematical difference between functions and operations, so square roots, logarithms, etc., are also operations. Still, we use the term operation for basic operators like addition, subtraction, etc.
What Is an Operation?
Operation is a process of performing calculations and determining solutions using mathematical strategies and methods. For performing an operation, we have to take some input values, and as a result, the output is produced. There are various kinds of operations used in mathematics.

Figure 1 – Some Mathematical Operations
Some common operations are addition, subtraction, multiplication, and division. These four operations are the basic arithmetic operations and the building blocks of mathematics. Squaring, square root, cube root, logarithms, etc., are also mathematical operations.
Operands
An operand is a value on which an operation is to be performed. It is basically the object of the operation. An operand can be any number or variable. For example, 3+2=5 is an equation; in this equation, 3 and 2 are the operands, and addition is the operation performed on these operands.
Operator
An operator is a symbol that represents a specific operation. Operators tell us how to manipulate numbers and extract solutions. Operators are important in performing operations.
Without operators, one cannot solve any type of function or equation. ‘+’ is the operator for addition, ‘-’ is the operator for subtraction, ‘x’ is the operator for multiplication, ‘÷’ is the operator for division and ‘=’ is an operator for equals to.
Addition
It is a mathematical process in which numbers, values, or things are combined and counted together. The numbers that are going to be added are called addends, and the outcome of their addition is called sum.
The symbol for representing addition is ‘+,’ or in other words, + is the operator for addition. It is written as 4+6 and read as ‘four plus six.’ The order of the numbers doesn’t matter in performing addition; hence addition is a commutative process.
Zero is the only numeral when added to any number; it does not change the identity of the actual number. So, zero is the identity element for addition. It is also typical for the associative property. Addition is one of the most important functions of mathematics that is widely used in studying mathematics as well as in daily life.
Addition can be performed on any kind of number, whether integers, complex numbers, fractions, decimals, or real numbers. There are some rules to remember while adding integers, i.e., if we have to add two positive numbers, the answer will be a positive number.
If the addition is taking place between two negative numbers, we get a negative answer. The addition of a positive and negative number will subtract the numbers with the sign of the largest number.
The following examples will make it easy to understand addition more effectively
- 4 + 5 = 9
- -4 – 5 = -9
- -4 + 5 = +1
- -5 + 4 = -1
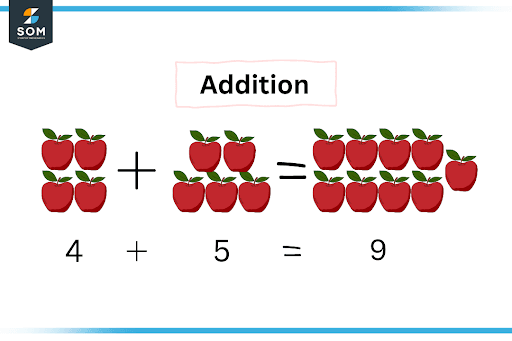
Figure 2 – Adding 4 apples to 5 apples gives total of 9 apples
Subtraction
It is a mathematical operation that takes away some values from the total number. Subtraction is used when we want to eliminate anything from the whole. Another name for subtraction is the difference.
The number from which the value is to be subtracted is called minuend. The number being subtracted is called subtrahend. The answer so produced is the difference between the two numbers. It is represented by a negative symbol ‘-’ known as the minus sign, written as 6-3 and read as ‘six minus three.’
Subtraction is an inverse operation to that of addition. Subtraction makes the number smaller, whereas addition makes the number larger. Order of the numbers is important for subtraction; hence it is not commutative. 5-3 is not equal to 3-5. Both of these functions produce different answers.
Subtraction can also be executed on complex numbers, integers, decimal numbers, fractions, etc. It is also an important mathematical operation that is widely used.
Subtracting a positive number from a positive number produces a positive answer. If we subtract two negative numbers, the answer will be a negative number, but they will be added, not subtracted. When a positive and a negative number are subtracted, the answer will have a sign of the largest number.
Have a look at the following examples to understand subtraction more efficiently
- 6-4=2
- -6-(+4)=-10
- -6-(-4)=-6+4=-2
- -4+6=2

Figure 3 – A visual representation of the subtraction operation
Multiplication
It is also an important arithmetic operation. Multiplication is an operation that gives the answer by repeating the addition process. It basically portrays repeated addition. If we want to add a number multiple times, it is better to multiply it a single time.
Multiplication gives a sudden increase in the number. Multiplicand and multiplier are the two factors of the multiplication process. The result we get after multiplying two or more numbers is called the product. It is denoted by a small cross sign ‘✕’ or asterisk sign ‘*’ or a dot. 4 ✕ 5 is read as ‘4 multiplied by 5’ or ‘4 times 5’.
Zero absorbs the identity of the number and produces a zero if multiplied by any number. 1 has a special property that if it is multiplied by any number, it gives the same number as the answer. 1 does not change the identity of the actual number; hence 1 is the identity element for multiplication.
Multiplication is a commutative as well as an associative process. If we apply a multiplication operation to two negative numbers, the answer will be a positive number.

Figure 4 – A visual representation of multiplication operation
Division
It is a process that divides the number into equal parts. It is the inverse or opposite process of multiplication. Division breaks a bigger number into equal smaller numbers. It is also a significant arithmetic operation. The division operation is represented by ‘÷’ and ’\’ and read as ‘divided by.’
The number on which the division process is taking place is the dividend. The number that divides the dividend is the divisor, and the answer to the division is called the quotient. Sometimes, the numbers are not completely divided, and some number is left over, which is called the remainder.
If a number is divided by zero, the answer is undefined. Dividing a number by itself will give the answer 1. There is an interesting fact about 1: if any number is divided by 1, the answer will be the same number because 1 doesn’t affect the identity of the number. Zero divided by any number gives zero.

Figure 5 – A visual representation of division operation
Order of Operations
The order of operations is the method or steps to solve an expression. It tells us the sequence of solving any mathematical expression. If an expression has identical operations, the sequence of solving that expression will be from left to right.
But if an expression has multiple operations, then we need a proper method to solve them; otherwise, the answer will be incorrect. This order is recognized as PEMDAS, where P stands for parentheses, E for exponents, M for multiplication, D for division, A for addition, and S for subtraction.
It is also known as BODMAS, where B stands for brackets, O stands for order, i.e., exponents, powers, etc., and DMAS are the four basic arithmetic operations.
- Firstly, the operation inside the parentheses or brackets has to be solved. There is a certain order to solve the parentheses, i.e., the round brackets ( ) first, then curly brackets{ } and then box brackets [ ].
- Now comes the turn of the exponential expression. If there is an exponent used in the given algebraic expression, it has to be solved after parentheses.
- For the next step, any one of the multiplication and division can be solved first, depending on the rule of left-to-right solving. The operation that comes foremost in moving from left to right will be solved initially.
- Similarly, for addition and subtraction, the operation that comes first in moving from left to right will be solved first.
Let us consider an expression 10 ÷ (3 + 2) * 4 + 3$^2$ + 6 – 9 and solve it using the order of operations.
Parentheses first, 10 ÷ 5 * 4 + 3$^2$ + 6 – 9
Solve the exponent 10 ÷ 5 * 4 + 9 + 6 – 9
The division is the first one from left to right, so solving it, we get 2 * 4 + 9 + 6 – 9
Now multiplication, 8 + 9 + 6 – 9.
Solving from left to right, 17 + 6 – 9.
Again repeating left to right rule 23 – 9.
The answer is 14.
Solved Examples Involving Different Operations
Example 1
Add 16 and 20 and subtract 11 from the sum.
Solution
Adding 16 and 20, we get 36.
Subtracting 11 from 36 gives 25.
Hence, 25 is the answer to the given problem.
Example 2
Evaluate the solution of the expression (7-√9) * (6$^2$ – 9 + 2).
Solution
=(7 – 3) * (36 – 9 + 2)
Solving both parentheses simultaneously.
= (4) * (27 + 2)
= 4 * 29
= 116
All images are created using GeoGebra.
