Open Interval|Definition & Meaning

Notation

Open interval is generally represented with parentheses. Thus, the open interval between a and b, where a is less than or equal to b, would be represented as (a, b). Another less common notation for the same interval is ]a, b[. 

In set notation, the same interval would be represented as:

{x : a < x < b} 

An open interval can also be represented on a number line. The following number line shows an open interval between 1 and 6. Note that the endpoints are represented with hollow circles.  

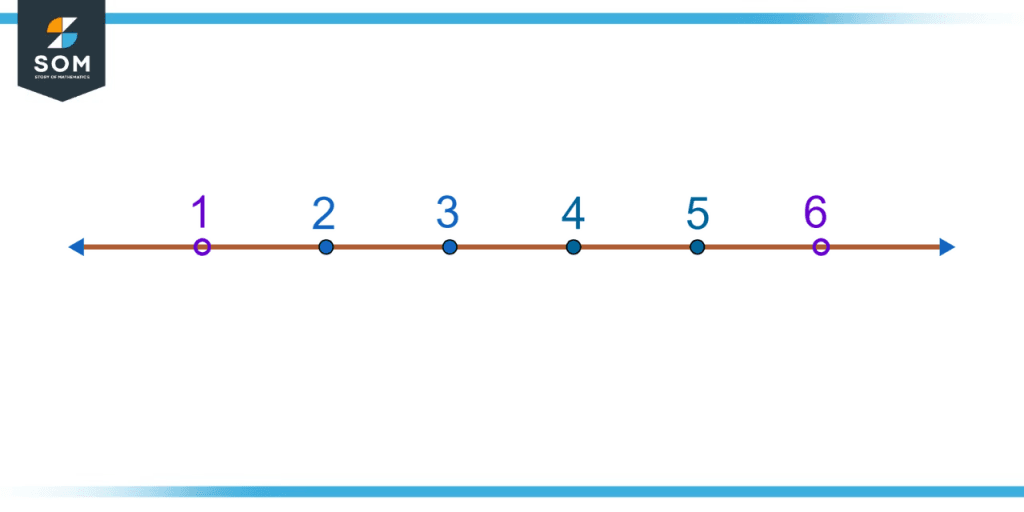
Figure 1 – Representation of open interval between 1 and 6 on the number line.

Properties

• The set of all real numbers is an open interval since it contains all the numbers between negative infinity and positive infinity but does not contain either infinites – since they are not real numbers. This is represented as (-$\infty$, $\infty$).
• A half-open interval is open from one side and closed from the other side. This means that one of the endpoints will be part of the interval and the other endpoint will be excluded. 
• An open interval with the same start point and end point represents an empty interval. For example, (b, b) represents an empty interval since no number exists greater and lesser than b which is not equal to b. 
• The midpoint of an interval with endpoints a and b is given by the mean of endpoints i.e., (a+b)/2.

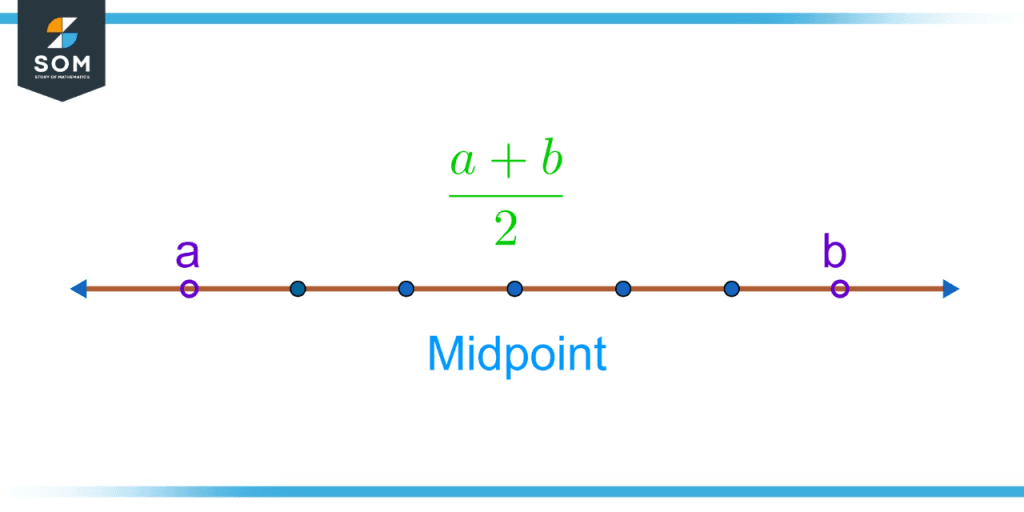
Figure 2 – Midpoint of the open interval between a and b.

Operations

Intersection

In set theory, intersection is the operation of finding the common elements of the operands. For intervals, Intersection is the operation of finding the common interval lying in all the operand intervals. Intersection can be found for two or any higher number of intervals. For two intervals, (a,b) and (c,d) their union is denoted by (a, b) $\cap$ (c, d) and given by:

(a, b) $\cup$ (c, d) = {x | a < x < b & c < x< d}

Note that for the two intervals such that a < b and c < d, their intersection will only be a non-empty set when c < b.  

Note that the commutative property holds for the intersection of intervals since (a, b) $\cap$ (c, d) = (c, d) $\cap$ (a, b). 

Union

Union is another basic operation in set theory that gives the elements that belong to any of its operands. The same concept is extended to the union of intervals as well. Union of two intervals results in a interval that is the combination of both the interval. Depending upon the endpoints of the intervals, union of intervals can result in a interval that is discontinuous. 

Union of two intervals (a, b) and (c, d) is denoted by (a, b) $\cup$ (c, d) and is given by:

(a, b) $\cup$ (c, d) = {x | a < x < b or c < x < d}

Note that the commutative property holds for the union of intervals since (a, b) $\cup$ (c, d) = (c, d) $\cup$ (a, b). 

Difference

The difference of the two intervals is the operation that results in an interval that is a part of the first interval but not part of the second interval. In other words, part of the first interval which is also present in the second interval is removed to find the difference. 

It should be noted that if the intersection of the intervals is an empty set, meaning no common part exists between the intervals, their difference will simply be equal to the first interval. 

Another boundary case for the difference exists when the first interval is a subset of the second interval. Since all the values of the first interval are also part of the second interval, their difference will result in an empty interval. 

Complement

The complement of an interval consists of all the values that are not part of the interval itself. Since the endpoints of an open interval are not part of the interval, the complement of the interval will contain the endpoints as well. 

For an open interval (a, b), its complement is given by:

{x | x $\leq$ a , x $\geq$ b}

A Few Examples on Open Intervals

Example 1

Consider two intervals A = (3, 8) and B = (5, 12). Write the elements of both intervals and find their union, intersection and difference. 

Solution

Both the given intervals are open intervals since they are given in the parentheses notation. Thus, they contain the elements in between the endpoints without including the endpoints. 

In set notation, A can be expressed as:

A = {x | 3 < x < 8}

Which can be expanded to obtain the elements of A:

A = {4, 5, 6, 7}

Similarly, the interval B is given as:

B = {x | 5 < x < 12}

With elements of B as:

B = {6, 7, 8, 9, 10, 11}

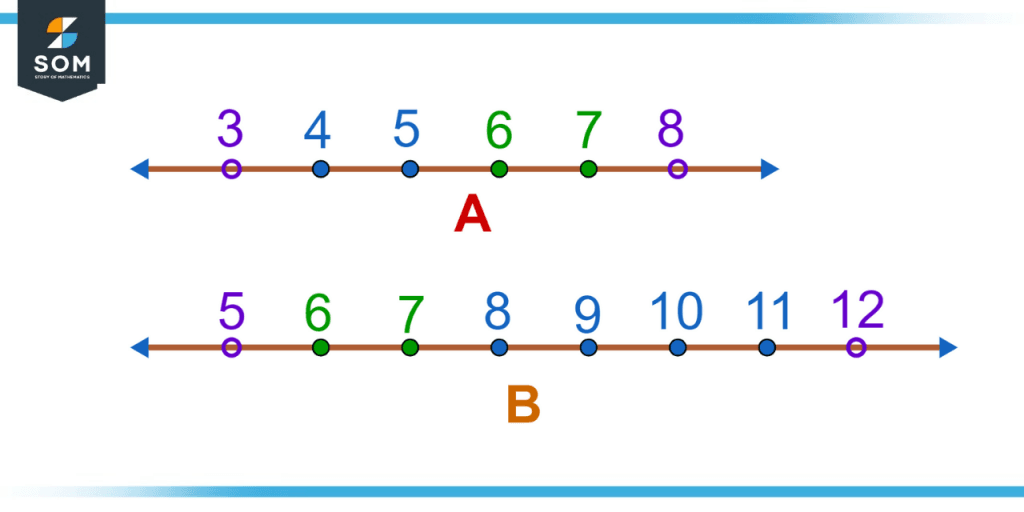
Figure 3 – Representation of the intervals on number line.

The union of intervals gives the elements that are part of at least one interval. For the given intervals, this consists of the following elements:

A $\cup$ B = {4, 5, 6, 7, 8, 9, 10, 11}

The intersection of intervals consists of elements that are part of both intervals. For the given intervals, this consists of the following elements:

A $\cap$ B = {6, 7}

The difference consists of the elements that are part of the first interval but not part of the second interval. The difference of A and B is given by:

A – B = {4, 5}

The difference between B and A is given by:

B – A = {8, 9, 10, 11}

Note from the above that the difference operator does not have the commutative property since A – B is not equal to B – A. 

Example 2

A student makes several measurements for the mass of a small bag. All the measurements lie closely and below 100 grams. Represent the mass of the bag in the form of an open interval. 

Solution

The mass of the bag must be greater than zero since it cannot be zero. From the given problem statement, the mass of the bag is also less than 100 grams. This means that the value of the mass lies in an interval, without the endpoints included – 0 and 100 grams. 

We know that when the endpoints of the interval are not included, this forms an open interval. Hence the given situation can be represented in the form of an open interval. Recall that an open interval is represented in the form of (a, b) where a and b are the endpoints of the interval. For the given situation, the endpoints are 0 and 100 respectively. Thus, this can be represented as:

(0, 100)