JUMP TO TOPIC
Interpolation|Definition & Meaning
Definition
Interpolation is the process of creating a new value based on the values already present in a set of data. One further way to explain it is to think of it as the act of putting in or interjecting a value that is somewhere in the middle of two other values.
The process of fitting the data points to the value of a function is known as interpolation.
It can be utilized in a wide range of technical and scientific applications, such as the construction of new data points within the bounds of a discrete data set of existing data points or the calculation of the formula for the function that will flow from the given set of points (x,y).
We will go into great detail about interpolation’s definition, formulas, and applications in statistics in this post.
Figure 1 – Interpolation of two points
Explanation of Interpolation With an Example
Interpolation is the process of deriving a new value from the current values in a data collection. The act of injecting or interjecting some intermediate value among two other values is another way to describe it.
Interpolation in data science and mathematics involves computing the value of a function depending on the values of many other data points in a particular sequence. This function can be expressed as f(x), as well as the range of known x values is xo to xn.
Consider, for instance, a regression line with the equation y = 3x + 4. To construct this “best-fit” line, we know that the value of x must be between 0 and 10 Suppose that we select x = 6 We may estimate the value based on the best-fit line and equation.
The following figure represents the interpolation of sin wave between two points A and B.
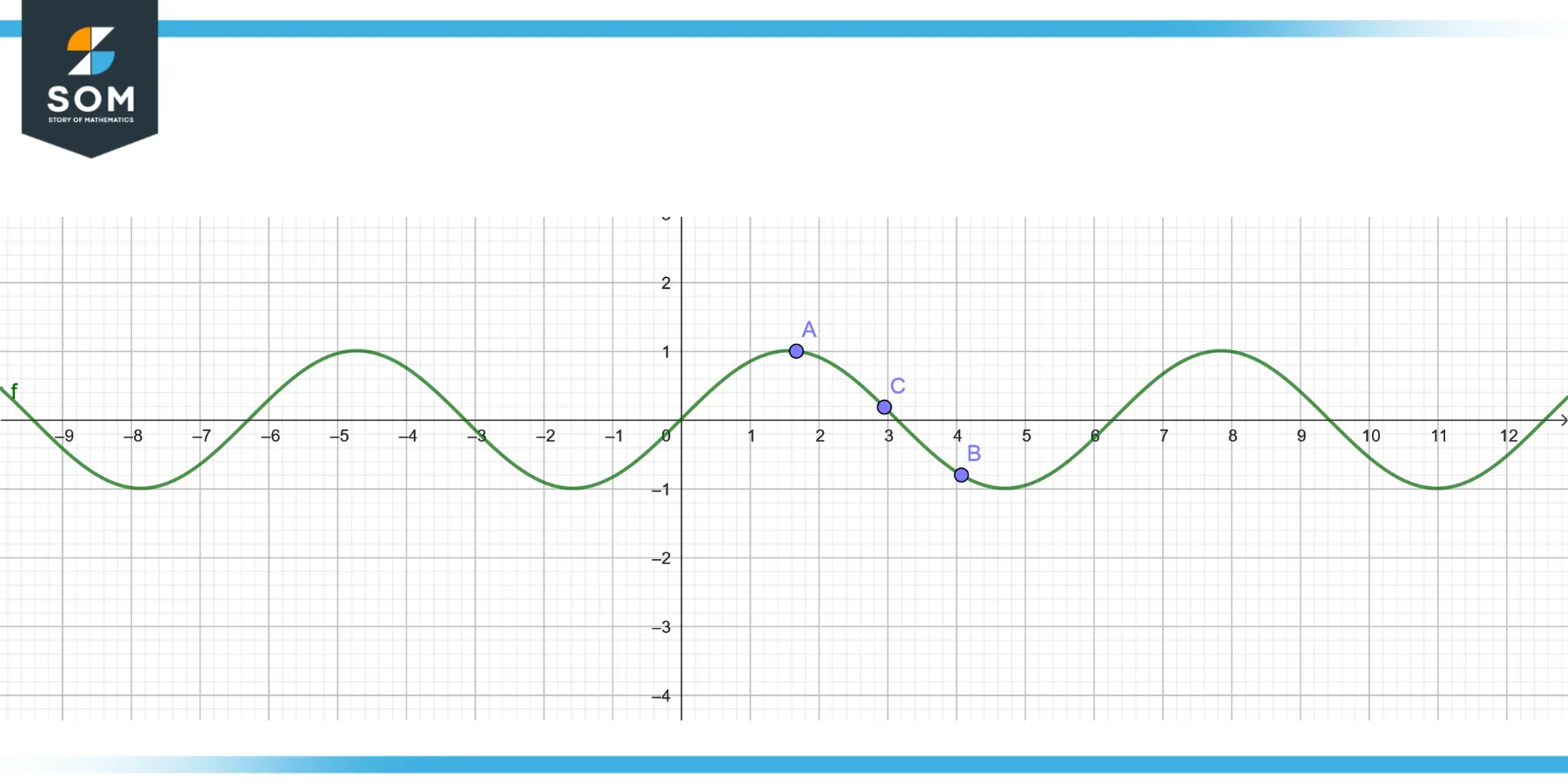
Figure 2 – Interpolation of a sine wave
The illustration below represents the cos wave with interpolation between two points on cos wave.
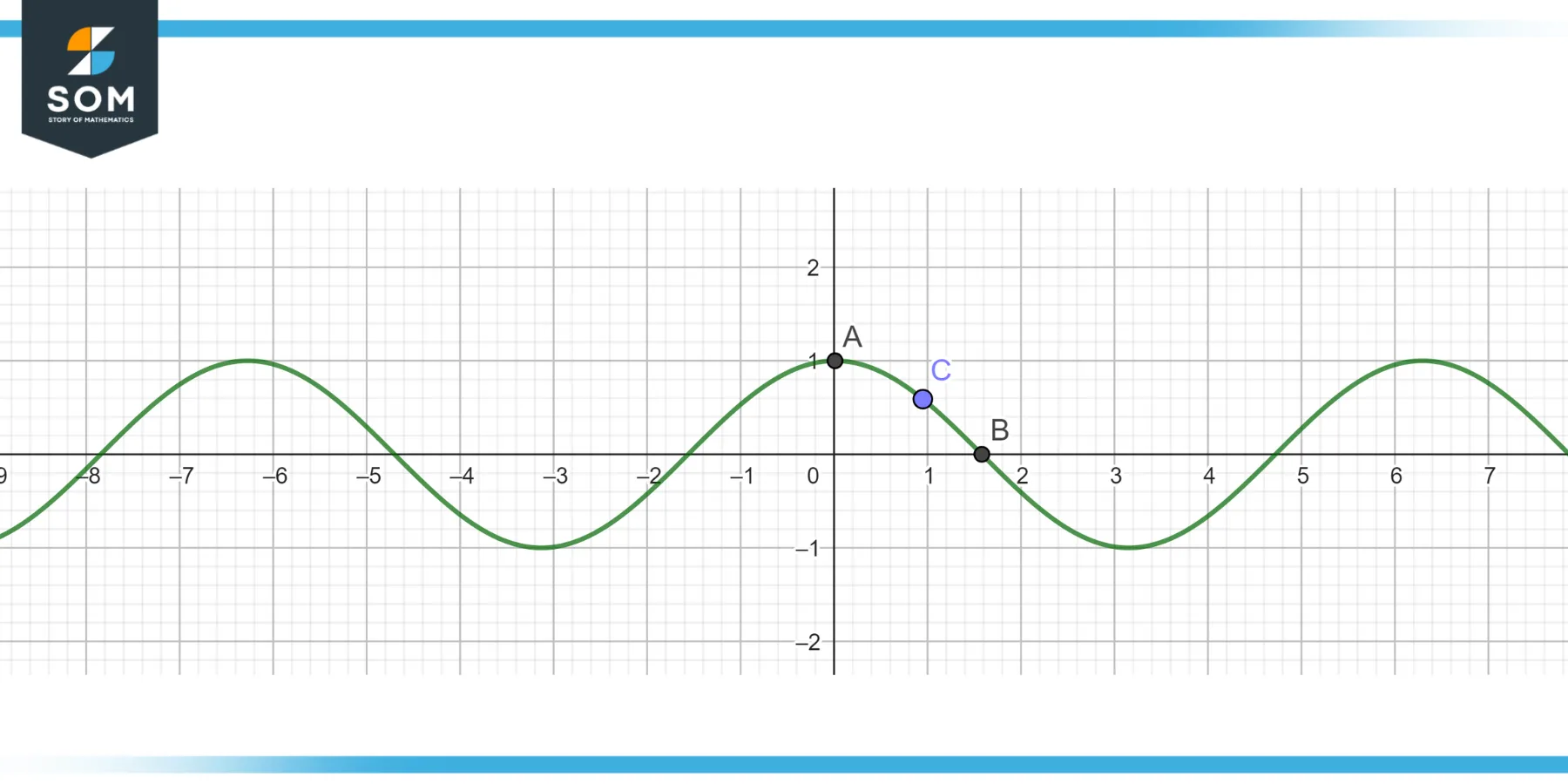
Figure 3 – Interpolation on a cosine wave
What Is the Difference Between Extrapolation and Interpolation?
Extrapolation is the estimation of an unknown value by extending a series of known values or facts. To draw a conclusion that is not directly supported by the available evidence is to engage in the process of extrapolation. Interpolation is the estimation of a value that exists between two known values in a set of values.
Standard Interpolation Techniques
The following are the three most prevalent interpolation methods:
- Interpolation linearization
- Polynomial interpolation
- Spline interpolation
Interpolation Linearization
Interpolation using linear relationships is one of the simplest methods available. In this part of the process, two points on such a graph are used to calculate the other values by drawing a straight line between them. Estimates are typically flawed when a straightforward approach is utilized.
Polynomial Interpolation
Polynomial interpolation is a method for estimating the values of missing data points in a data collection by plotting polynomial functions on a graph. It is a method that is both more precise and accurate. The graph of the polynomial completes the curve by filling in the gaps between known points so that data can be found between those locations.
There are many different approaches to polynomial interpolation, including the following:
Polynomial interpolation is a method for estimating the values of missing data points in a data collection by plotting polynomial functions on a graph. It is a method that is both more precise and accurate. The graph of the polynomial completes the curve by filling in the gaps between known points so that data can be found between those locations.
There are many different approaches to polynomial interpolation, including the following:
- Lagrange interpolation
- Interpolation using Newton’s method, polynomial interpolation, and spline interpolation
Newton’s split differences interpolation polynomial is another name for the procedure that is commonly known as the Newton method.
The Lagrange and Newton interpolation methods both provide the same result, which is a polynomial function that has the lowest feasible degree and is able to pass through all of the data points in the set. This is known as the smallest polynomial function.
However, the computations that are used to arrive at the identical conclusion by the two methodologies are rather different.
Spline Interpolation
Piecewise functions are put to use in the process of spline interpolation in order to make estimates for values that are absent from a data set and to complete it.
The Lagrange & Newton methods estimate a single polynomial that applies to the full data set. Spline interpolation, on the other hand, defines numerous simpler polynomials that apply to different subsets of the data. Because of this, it is often thought to offer more detailed findings and is regarded as a procedure that is more reliable.
Methods of Extrapolation That Are Commonly Used
The following are examples of three of the most prevalent types of extrapolation methods:
- extrapolation along a linear path
- polynomial extrapolation
- conic extrapolation
A technique that is very similar to linear interpolation, linear extrapolation includes drawing a straight line and making use of a linear function to make predictions about values that are not contained within a data set.
Polynomial extrapolation is a method that determines the values on a graph by using polynomial forms and functions.
The process of determining unknown values by employing conic sections that already have data for them is called conic extrapolation.
Interpolation Example in Real Life
Interpolation is useful if items need to be scaled up or down. Perhaps you are familiar with the catering costs for events with 10 guests, 50 guests, and 100 guests, but you require an accurate estimate for events with 25 or 75 guests. This is a useful fact to have while throwing a party.
Or maybe you’re an entrepreneur whose tiny business is suddenly expanding. It is professional to anticipate what you will require as you expand your organization.
How many new employees have been hired? How large is the room? Who is responsible for cleaning this area? How long will it take to clean the space? How much longer would it take to complete tasks with more employees? What will you be able to accomplish in a day? These questions might all be solved by interpolation.
Perhaps you work as a server in a restaurant. You need not only a good concept of how long it takes the kitchen to prepare food for your clients, regardless of their number.
Additionally, you should have a solid concept as to how it takes the group to consume meals so that you may check on them during the proper moment. This is an example of interpolation.
Acquiring an automobile. How much money will you invest in a vehicle with a given amount of miles? Will it be beneficial? Could you afford it? This is an example of interpolation.
A Numerical Example of Linear Interpolation
Example
Determine the value of the unknown variable by computing it using the interpolation equation found in the data set. Consider the following scenario: the value of X is 60. What is the y value in this case?
Solution
With the use of interpolation, we can get the value of Y when X is 60 using the following formula: –
Y = Y1 + [ (Y2 – Y1) / (X2 – X1) ] * (X – X1)
X has been set at 60, and it is now necessary to find Y.
Y = Y1 + [ (Y2 – Y1) / (X2 – X1) ] * (X – X1)
= 80 + [ (120 – 80) / (70 – 50) ] * (60 – 50)
= 80 + (40/20) * 10
= 80 + 2*10
= 80 + 20
= 100
All mathematical drawings and images were created with GeoGebra.
