JUMP TO TOPIC
Interest|Definition & Meaning
Definition
Interest is the additional amount on top of the principal amount that a financial institution or a borrower pays to the depositor or lender at a specific rate.
It is the price of borrowing money, paid or charged over some period of time.
It is usually expressed as a percentage.
Figure 1 demonstrates the concept of interest.
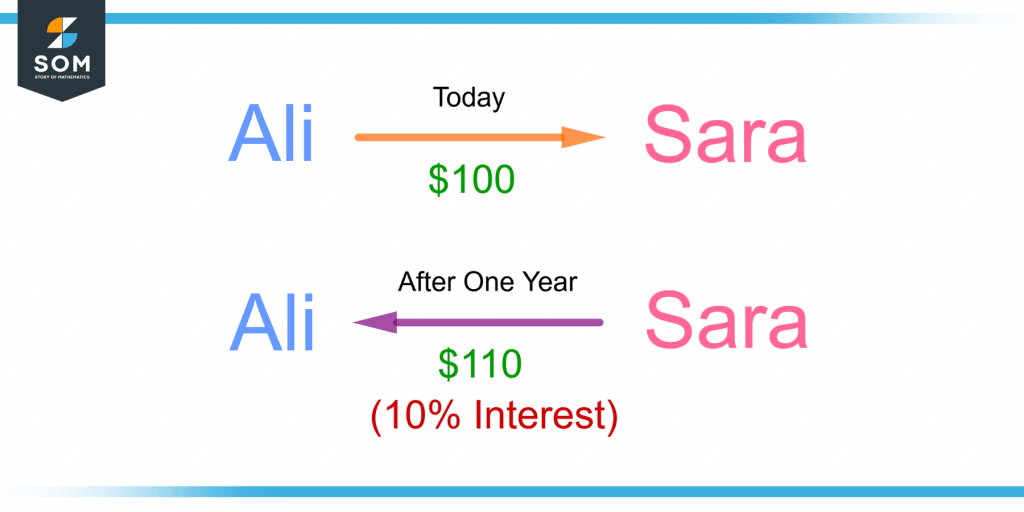
Figure 1 – Demonstration of Interest
Sara took 100 dollars from Ali at 10% annual interest. After a year, Sara had to pay Ali $100, and $10 which is the 10% interest. So, she had to pay $110.
Interest refers to the concept that money is not free to borrow. The more time passes on the loan or deposit, the more interest accumulates on it.
The interest on the initial amount borrowed or lent depends upon the interest rate, the principal balance, the total time for which it is deposited or lent, and the compounding frequency.
Interest Rate
The interest is usually written as a percentage known as the interest rate. It is the rate of interest applied to the initial principal amount a borrower takes from a lender due some time.
The interest rate can be fixed or variable.
Fixed Interest Rate
A loan with a fixed interest rate has the same interest rate throughout the life of the loan. It is usually higher than the variable interest rate.
Variable Interest Rate
A variable interest rate varies over the time of the loan. It starts with a percentage usually smaller than the fixed interest rate and increases or decreases with time. It depends upon an index that fluctuates with time.
Figure 2 shows the comparison of fixed and variable interest rates through a graph.
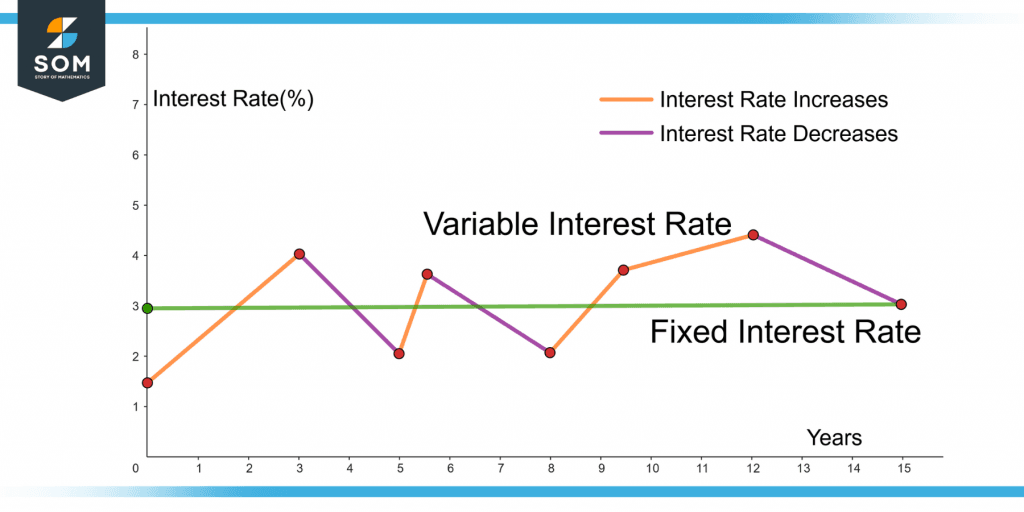
Figure 2 – Comparison of Fixed and Variable Interest Rates
Important Terminologies Related to Interest
In economics and finance, some critical terminologies related to interest are described below.
Investment
An investment is an amount of money given to a bank or financial institution to gain some profit on it. It is the first deposit on which interest is added later as a profit.
Borrower
A borrower is a person who borrows money from someone to return it. The money is taken on the condition of returning the initial amount with a pre-determined interest.
Lender
A lender is a person who loans money to a person or a company with the presumption that the borrower will repay the funds. It can also be a financial institution such as a bank that wants repayment with interest.
Principal Amount
The principal is the initial amount borrowed from a lender on which the interest is applied. This term is used while dealing with simple or compound interest. It can be a loan or an investment in a bank.
It is also known as the “principal sum”.
Figure 3 shows the demonstration of these terms related to interest.

Figure 3 – Demonstration of Lender, Borrower and Principal Sum Related to Interest
Types of Interest
The two types of interest are explained as follows:
Simple Interest
Simple interest involves applying interest on the principal amount paid after the due course of time.
The borrower has to pay the principal amount plus the interest on the principal and so on. The formula for simple interest is as follows:
A = P(1 + rt)
Where A is the final amount after time t has passed and P is the principal amount. The time t passed on the principal sum is in years.
Annual interest rate is the interest rate applied after a year on the loan borrowed or investment deposited and is denoted by r. This percentage is converted into decimal before placing in the equation by dividing it by 100.
Figure 4 shows an example of simple interest with an annual interest rate of 5% on a principal of $10,000 over 3 years.
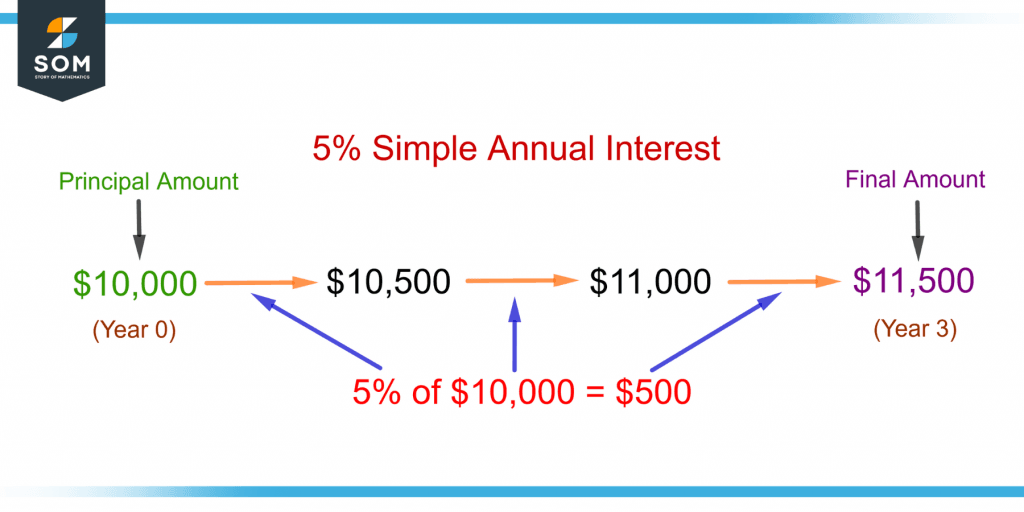
Figure 4 – Illustration of Simple Annual Interest
If the period extends to 9 years in the above example, the final amount can be calculated as follows:
A = 10,000[1 + (0.05)(9)]
A = 10,000[1 + 0.45]
A = 10,000[1.45]
A = $14,500
Compound Interest
Compounded interest involves having interest on the principal amount and the interest accumulated previously. It refers to the concept of “interest on interest” unlike simple interest.
The principal now becomes the previous principal plus the interest earned on which more interest is applied.
Periodic compounding deals with compounded interest over a period. The compound interest can be calculated by using the formula:
\[ A = P { \Big[ 1 + \frac{R}{n} \Big] }^{nt} \]
Where P is the principal sum, A is the final amount, R is the interest rate and t is the time passed in years.
The number of times interest is received in a year is “n”. Its value depends upon the period the annual interest is compounded. Table 1 shows the value of n for the annual interest compounded over different periods.
| Compounded Time Periods | Value of “n” |
| Annually | 1 |
| Semi-annually | 2 |
| Quarterly | 4 |
| Monthly | 12 |
| Weekly | 52 |
| Daily | 365 |
For example, if a 10% annual interest is compounded semi-annually, the interest received after half a year will be according to 10/2 = 5% interest rate.
Figure 5 shows the example of figure 4 for compound interest.
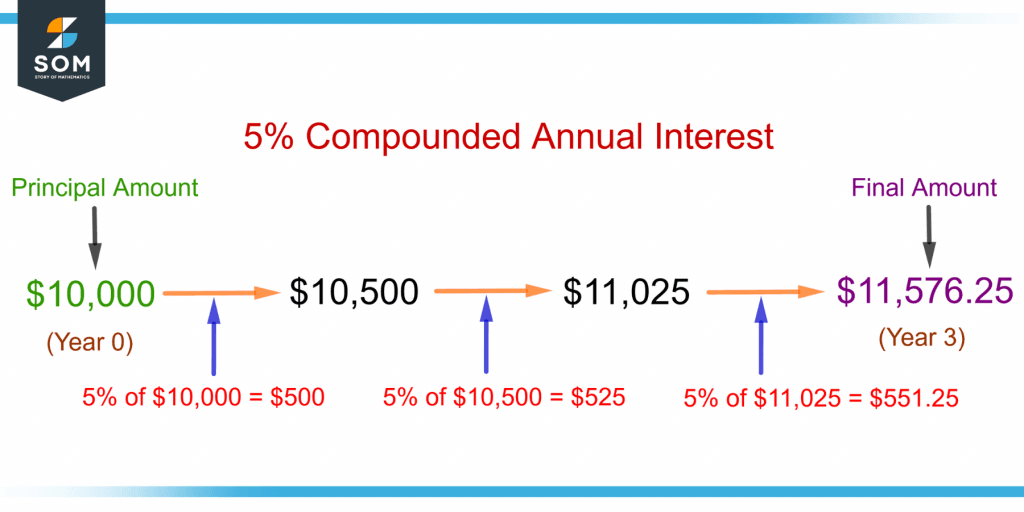
Figure 5 – Illustration of Compounded Annual Interest
For 9 years, the amount will accumulate to
\[ A = P { \Big[ 1 + \frac{R}{n} \Big] }^{nt} \]
\[ A = 10,000 { \Big[ 1 + \frac{0.05}{1} \Big] }^{(1)9} \]
A = 10,000 $[ 1 + 0.05 ]^9$
A = 10,000 $[ 1.05 ]^9$
A = 10,000(1.5513)
A = $15,513
Comparison of Simple and Compound Interest
From the same period of 9 years with a principal of $10,000 at a 5% annual interest, the final amount from receiving simple interest is $14,500 and from compound interest is $15,513.
Compound interest refers to exponential growth whereas simple interest applies linear growth. After a certain point, the money from compound interest overgrows increasing from the amount received from simple interest.
Example Problems Based on Interest
Example 1 – Simple Interest
Alina invests $6000 in a bank at an 8% annual interest rate. How much money she will receive after 14 years?
Solution
From the given data,
P = $6000, r = 8% = 0.08, t = 14 years
The final amount A will be:
A = P(1 + rt)
A = 6000[1 + (0.08)14]
A = 6000[1 +1.12]
A = 6000[2.12]
A = $12,720
Example 2 – Compound Interest
Simon deposits $50,000 in savings account with a 16% annual interest rate compounded quarterly. What will be the total amount in the account after 14 years?
Solution
The formula for periodic compounding is given as
\[ A = P { \Big[ 1 + \frac{R}{n} \Big] }^{nt} \]
Here
P = $50,000, R = 16% = 0.16, t = 14 years
As the annual interest is compounded quarterly, so n = 4.
Placing the values in the equation gives
\[ A = 50,000 { \Big[ 1 + \frac{0.16}{4} \Big] }^{4(14)} \]
A = 50,000 $[ 1 + 0.04 ]^{56}$
A = 50,000 $[ 1.04 ]^{56}$
A = 50,000(8.9922)
A = $449,610
So, the amount after 14 years will be $449,610.
All the images are created using Geogebra.
