Imaginary Number|Definition & Meaning

Even though it doesn’t exist on the number line and can’t be quantified, imaginary numbers exist and have mathematical applications. 

Representation of Imaginary Number

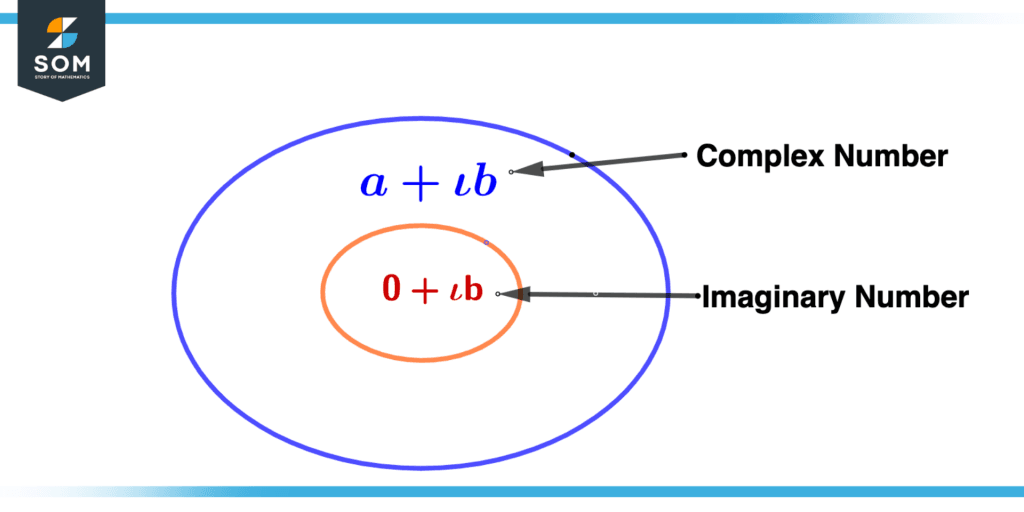
Figure 1 – Imaginary Number Representation

An imaginary number is represented by the greek letter “i,” which denotes the square root of negative unity. Generally, imaginary numbers are written as the product of some real number with the iota $i$ or simply i.

When combined with a real number a and an imaginary number bi,  a + bi forms a complex number, in which the real part a is called the real part of the complex number, and the imaginary part bi is called the imaginary part.

The imaginary unit is typically denoted by j instead of i in many engineering and control systems problems since i is mainly used to represent electric current.

Imaginary Unit

Consider the equation shown below. The solution of this quadratic equation can be generalized by taking the square root on both sides which gives:

x² = -1

\[\mathsf{\sqrt{x^2}=\sqrt{-1}}\]

x = $\mathsf{\sqrt{-1}}$

$\sqrt{-1}$ equals the imaginary unit we call iota (i, $i$ or sometimes j):

i = $\mathsf{\sqrt{-1}}$

Pure Imaginary Number  

It is possible to create infinitely many pure imaginary numbers by taking multiples of this imaginary unit i. We can better understand how these numbers relate to real numbers by taking the squares of these numbers. Using the number 4i as an example, let’s square it. We can square 4i just as we would expect given the properties of integer exponents.

Squaring 4i:

(4i)² = 16i²

Based on arithmetic,  i² = -1. The value of i is therefore equal to the square root of −1. A simple condition for a purely imaginary number is that its real part is equal to zero.

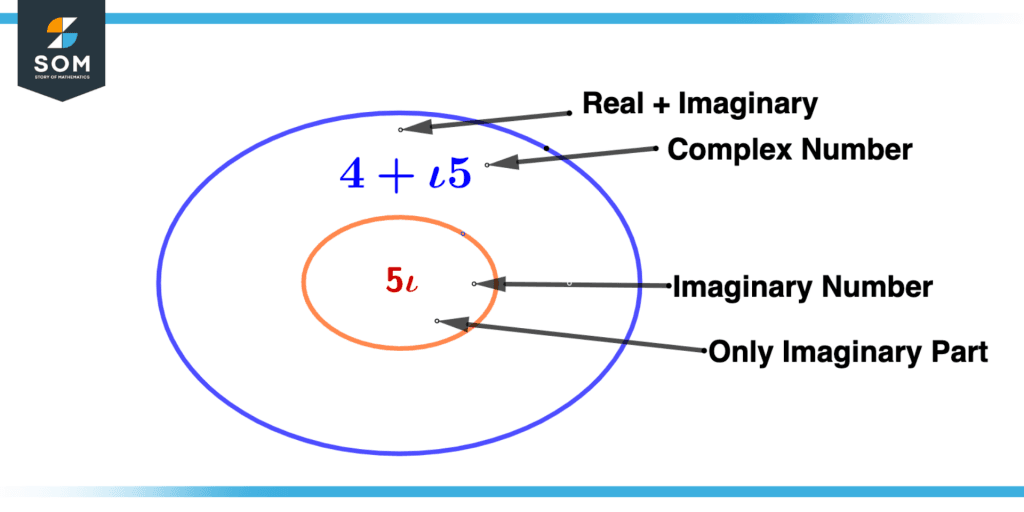
Figure 2 – Purely Imaginary Number Illustration

Value of Imaginary Unit 

Here we will discuss the different values of imaginary units.

In the particular case of the quadratic equation: z² = x, where x is a known value. One way of presenting its solution is as z = $\mathsf{\sqrt{x}}$. To calculate some imaginary numbers, we must follow the following rules:

• The value of imaginary unit i = $\mathsf{\sqrt{-1}}$
• The value of imaginary number i² is -1
• The value of imaginary number i³ is -i
• The value of an imaginary number having N power i^4N is 1

Graphical Interpretation of Imaginary Number

Imaginary numbers can be arranged perpendicular to the real axis because they lie on the vertical axis of the complex number plane. You can visualize imaginary numbers by considering a number line with positive magnitudes increasing rightward and negative magnitudes increasing leftward. Imaginary numbers increase in magnitude upwards when they are drawn on the x-axis, while imaginary numbers vary downwards when they are drawn on the y-axis.

The “imaginary axis” is sometimes referred to as this vertical axis and the horizontal axis is known as the “real axis”.Suppose we want to plot a purely imaginary number 2+2i then it will be 2 units in the vertical direction and 2 in the horizontal direction, this concept is illustrated in the figure below.

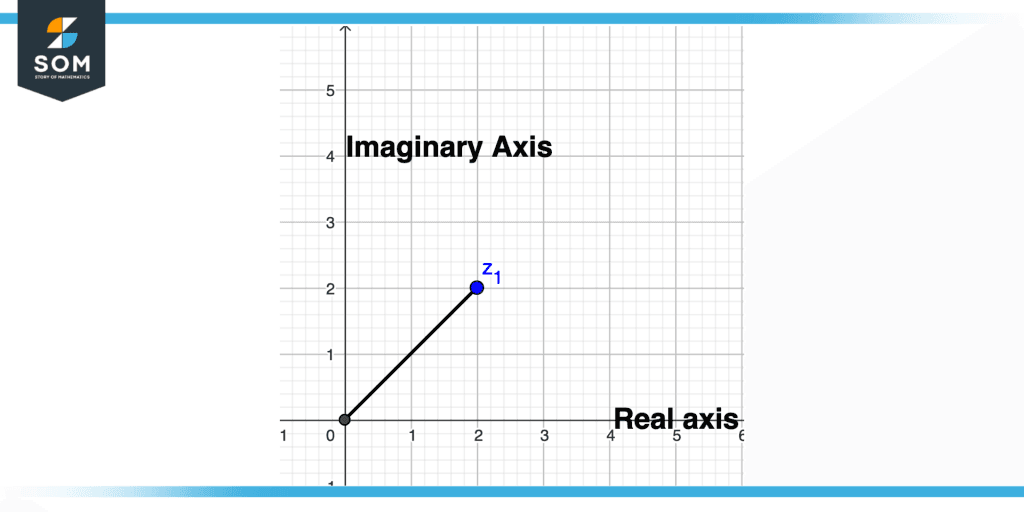
Figure 3 – Graphical Representation of Imaginary Number

Application of Imaginary Numbers

In Calculus and Signal Processing

Imaginary numbers, sometimes called complex numbers, are applied to real-life situations like quadratic equations and electricity. Equations that are not touching the x-axis are called imaginary numbers in quadratic planes. Advanced calculus often makes use of imaginary numbers. As well as cellular and wireless technology, imaginary numbers can also be applied to signal processing, a process that is useful in radar technology as well. In essence, imaginary numbers are used when measuring sine or cosine waves.

In Electrical Engineering

In electrical engineering, specifically in electronics that use alternating current (AC), imaginary numbers are especially useful. As a sine wave changes from positive to negative, AC electricity changes from positive to negative. Due to the fact that AC currents may not match properly on the waves, combining them can be very problematic. Calculating AC electricity and avoiding electrocution are made easier by using imaginary currents and real numbers.

Pairing Imaginary Numbers With Arithmetic Operations 

Addition

When two numbers involving imaginary numbers are being added to each other then the rule of thumb is that we have to add the real part to the real and the imaginary part to the imaginary.

Example: (x+iy) + (a+ib) = (x+a) + i(y+b)

Subtraction

The subtraction process follows the same rule as for addition real part should be subtracted from the real and the imaginary part from the imaginary.

Example: (x+iy) – (a+bi) = (x-a) + i(y-b)

Multiplication

The rule of thumb for multiplication is that the product of the real part (xa) should be subtracted from the product of the imaginary part (yb). This term as a whole will be considered as the real part of the result.

The imaginary term in the result will be equal to the sum of the product of the first term’s imaginary part with the second term’s real part (ya) and the product of the first term’s real part with the second term’s imaginary part (xb). 

Take a look at the following example to understand this:

(x+iy) (a+ib)=(x+iy)a+ (x+iy)ib

(x+iy)(a+ib)=(xa+iya+ixb+i²yb)

(x+iy)(a+ib)=(xa+iya+ixb-yb)

(x+iy)(a+ib) = (xa-yb) + i(ya+xb)

Division

For division, we will multiply the conjugate with both the numerator and denominator (the conjugate is basically the denominator with the imaginary part sign reversed). The conjugate of $a+bi$ is $a-bi$. In conjugate, since the sign of the imaginary part is reversed, the division process is illustrated below.

\[\mathsf{\frac{(x+iy)}{(a+ib)}=\dfrac{(x+iy).(a-ib)}{(a+ib).(a-ib)}}\]

\[\mathsf{\frac{(x+iy)}{(a+ib)}=\dfrac{(xa-yb)+i(ya+xb)}{(a^{2}-(ib)^{2})}}\]

\[\mathsf{\frac{(x+iy)}{(a+ib)}=\dfrac{(xa-yb)+i(ya+xb)}{(a^{2}+b^{2})}}\]

An Example of Operations on Imaginary Numbers

Show the multiplication, division, and plot of mathematical terms involving imaginary numbers. Consider the two imaginary numbers: 3+i, 2+i2.

Solution

Multiplication

(3+i)(2+2i) = (3+i)2 +(3+i)i2

(3+i)(2+2i) = (6+i2+6i+2i²)

(3+i)(2+2i) = (6+2i+6i-2)

(3+i)(2+2i) = (4+8i)

Division

\[\mathsf{\dfrac{(3+i)}{(2+i2)}=\dfrac{(3+i).(2-i2)}{(2+i2).(2-i2)}}\]

\[\mathsf{\dfrac{(3+i)}{(2+i2)}=\dfrac{(4+8i)}{(2^{2}-(i2)^{2})}}\]

\[\mathsf{\dfrac{(3+i)}{(2+i2)}=\dfrac{(4+8i)}{(4+4)}}\]

\[\mathsf{\dfrac{(3+i)}{(2+i2)}=\dfrac{(4+8i)}{(8)}}\]

Plot

3+i: We can clearly see it has to move 3 units in the real axis, which is the horizontal axis, and one unit in the imaginary axis, which is the vertical axis.

2+2i: We can clearly see it has to move 2 units in the real axis, which is the horizontal axis, and 2 units in the imaginary axis, which is the vertical axis.

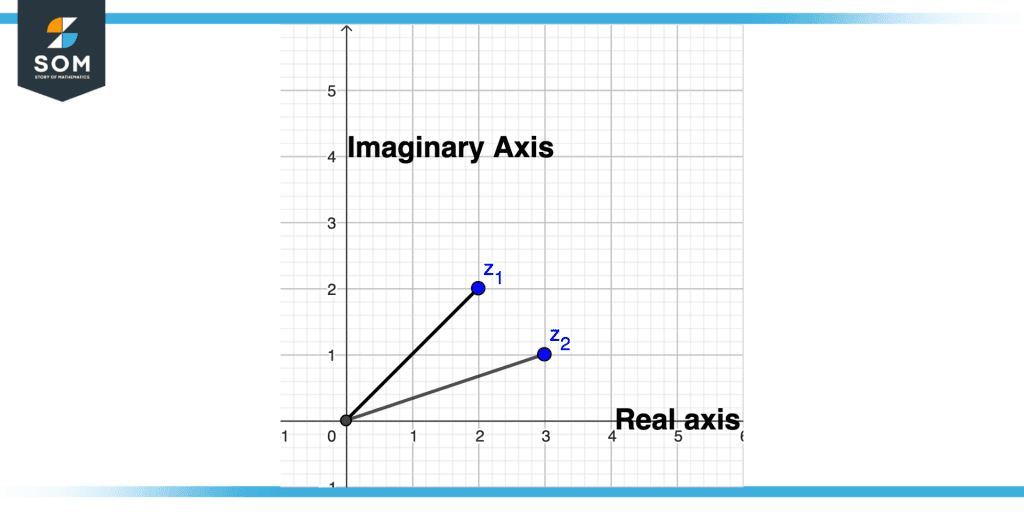
Figure 4 – Imaginary Number Plot Example

All mathematical drawings and images were created with GeoGebra.

Image Definition < Glossary Index > Imperial System Definition