Formula|Definition & Meaning

Notation 

A formula is usually written with an equal sign between the quantities. There must be a minimum of two quantities in a formula. There is usually a single quantity on the left side of the formula and one or more quantities on the right side. The quantity on the left side is called the subject of the formula.

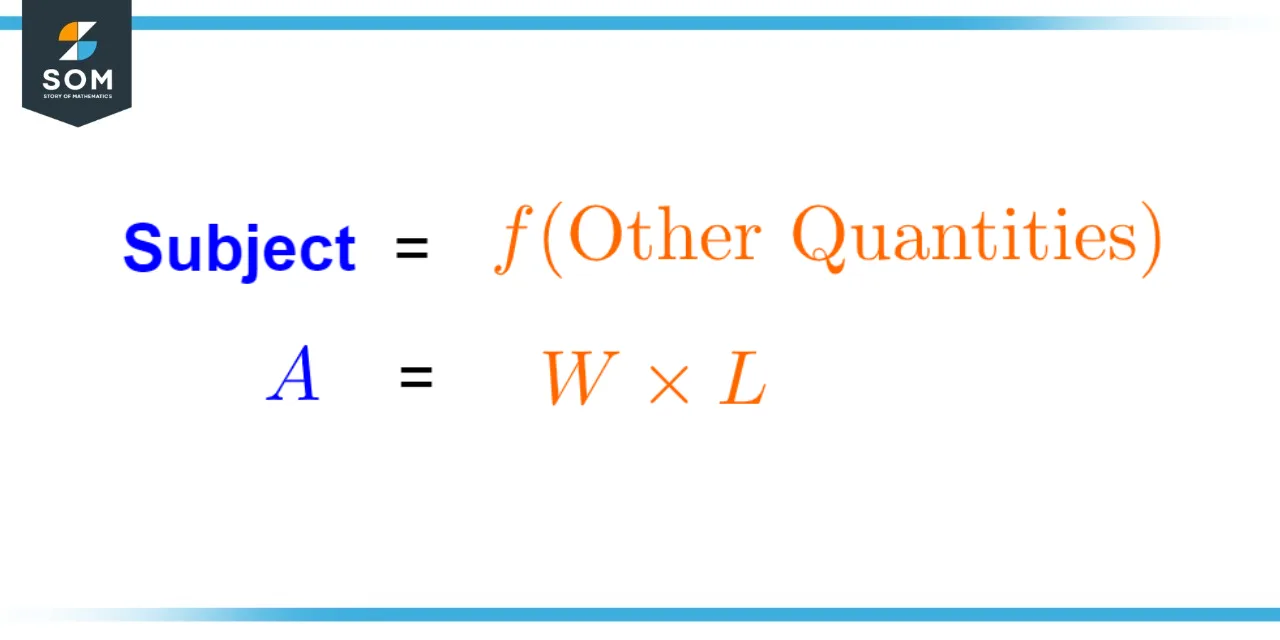
Figure 1 – Notation used for writing formulas.

The subject of a formula is basically the quantity that is being calculated through the given formula. For example, in the formula A = W x L for the area A of a rectangle with width W and length L, the formula calculates the area A through the quantities width and length of the rectangle. Thus, in the above formula, A is the subject of the formula and represents the quantity being measured.

Although most formulas contain the equal sign, it is also sometimes common to skip the equal sign and simply write the right side of the formula and describe the quantity obtained from the formula. For example, the formula for the area of a rectangle discussed above can also be written as W x L.

Change Of Subject

The subject of a formula can be changed to obtain a new formula for another quantity. This is extremely useful since the subject of a given formula is not always the desired quantity but might be a given or known quantity in a certain situation. In such a case, the desired quantity is made the subject of the formula by performing algebraic operations. 

The algebraic operations for changing the subject of a formula are similar to the steps involved in solving an equation. Thus, this procedure can also be termed as solving the equation – starting with the given formula – for the desired quantity. 

As the main objective of changing the subject is to express a formula in the form of a desired quantity being on one side, the operations involved are geared towards achieving this objective. All the other quantities are moved to the other side through algebraic operations, and the desired quantity is kept on one side. 

As an example of this, consider again the formula of the area of the rectangle discussed earlier. In the given formula, A is the subject of the formula. Consider a case where the area of the rectangle is a known quantity, but only one of the dimensions of the rectangle, say the length, is known. 

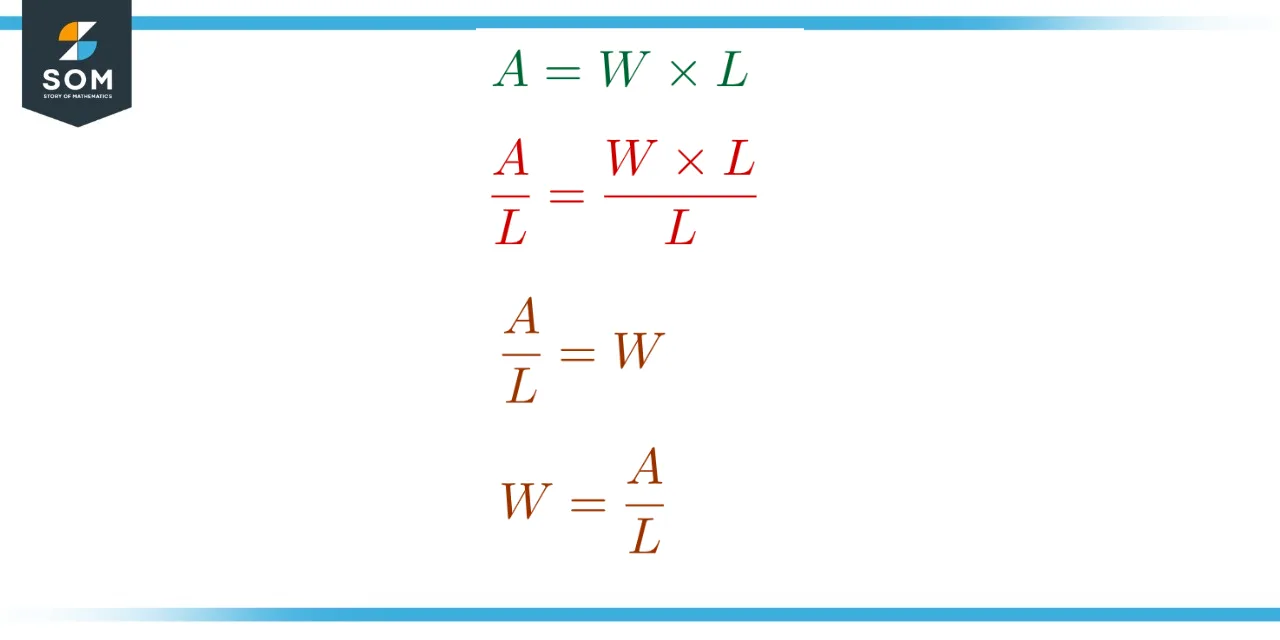
Figure 2 – Changing the subject to width in the formula for the area of rectangle.

In this case, width is the desired quantity and must be made the subject of the formula. Starting with the original formula of A = W x L, the width W can be made subject of the formula by dividing both sides by the length L and reflecting the quantities around the equal sign. This results in the formula W = A / L, in which the width W is the subject as desired. 

Some Common Formulas

Formulas are widely used in mathematics. A basic formula for the area of a rectangle has already been discussed above. Now we will discuss some other widely used formulas here. 

The formula for the square of the sum or difference of two numbers is a very basic algebraic formula and is widely applied. For two numbers a and b, such that their sum would be a + b, the square of the sum (a + b)² is given by a² + b² + 2ab. This can be represented in the form of a formal notation of a formula as:

(a + b) ² = a² + b² + 2ab

This formula is simply obtained by multiplying the sum a + b with itself by using the definition of the square of a number. The product is then simplified to obtain a concise formula which is shown above. The concise representation in the form of a formula makes it easier to directly use the resulting expression rather than having to perform the multiplication each time. 

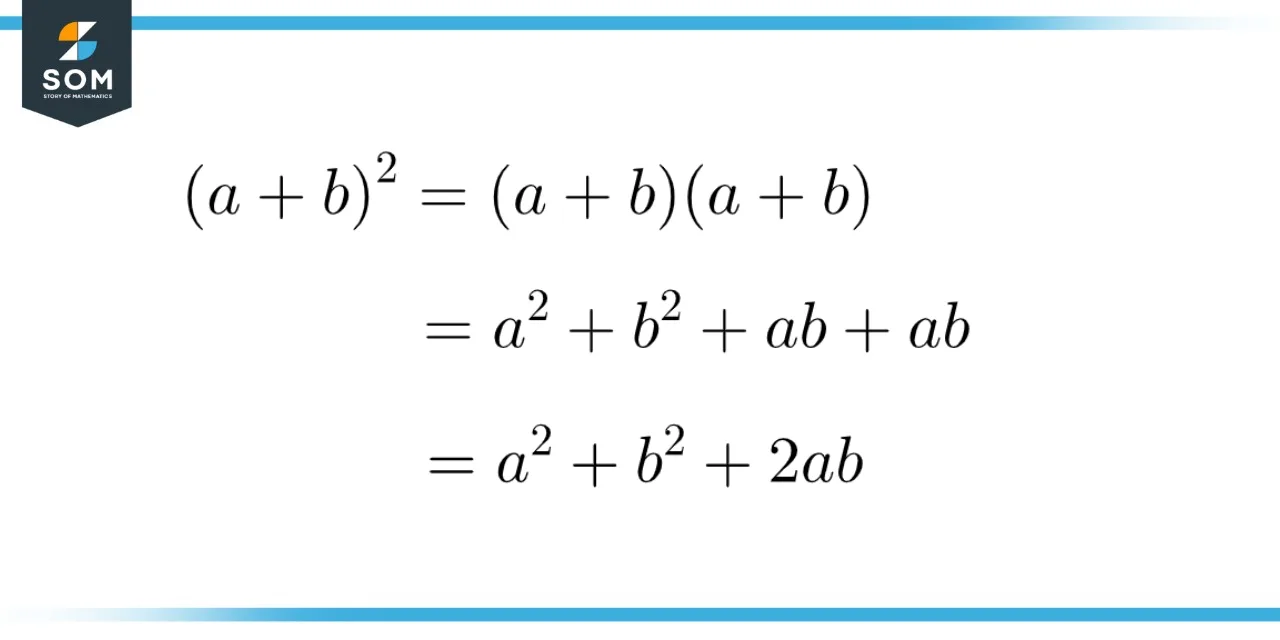
Figure 3 – Formula for the square of the sum of two numbers from the definition of a square.

Similarly, the square of the difference between the numbers a and b is given by:

(a – b)² = a² + b² – 2ab

A similar approach to that of the square of the sum of numbers can be used to obtain formulas for the cube of sum and difference of two numbers. These formulas are given by:

(a + b)³ = a³ + 3ab(a + b) + b³

(a – b)³ = a³ – 3ab(a – b) – b³

A triangle is one of the most basic geometrical shapes and one which is widely found in our daily lives as well. For this reason, the formula for the area of a triangle is an important one. For a triangle with base length b and height h, the area is given by half of the product of the base length and height. In the usual formula notation, this is written as:

Area = (1/2) $\times$ b $\times$ h

A right-angle triangle is a type of triangle having an angle of 90 degrees. One of the oldest formulas in mathematics involves the relationship between the sides of a right-angle triangle. For a right angle triangle with base a, perpendicular b, and hypotenuse c, the lengths are related by:

c² = $\sqrt{a^2 + b^2}$

This formula is called the Pythagoras’ formula for the work of the Greek mathematician Pythagoras who discovered this very important result as a part of the famous Pythagoras theorem. 

An Example Involving Formulas

John has obtained 78, 87, and 73 marks in his three exams. With the final exam still to go, he wants to know the minimum marks he needs to obtain in the fourth exam to obtain an average of at least 80. Use the formula for average to obtain the marks. 

Solution

The formula for the average of any set of numbers is given by the sum of numbers divided by the total count of the numbers. For the given situation, the set of numbers consists of the marks in different exams. Let the marks in the four exams be represented as a, b, c, and d where a, b and c are the given marks of three exams and d is the marks in the fourth exam. The average marks would be given by:

Average = (a + b + c + d)/4

4 in the denominator is obtained from the fact that there are a total of 4 exams. 

Now, the desired quantity in the above formula is the marks in the fourth exam d. So we need to change the subject of the formula and make d the subject. Start by taking the 4 in the denominator to the other side and multiplying:

4 * Average = a + b + c + d

Now, the marks in 3 given subjects can also be moved to the other side to obtain:

4 * Average – a – b – c = d

Reflecting the formula around the equal sign gives the desired subject:

d = 4 * Average – a – b – c

Substitute the values for average and marks in three exams and simplify:

d = 4 * 80 – 78 – 87 – 73

d = 320 – 238

d = 82

Thus, John needs to get a minimum of 82 marks in the fourth exam to keep his average over 80.

All mathematical drawings and images were created with GeoGebra.

Foot Definition < Glossary Index > Frequency Definition