JUMP TO TOPIC
Cross Section|Definition & Meaning
Definition
The cross-section is defined in geometry as the shape formed by the intersection of a solid and a plane. A three-dimensional cross-section is a two-dimensional geometric shape. In other words, a cross-section is a shape formed by cutting a solid parallel to the base.
Cross Section
A cross-section represents an object’s intersection with a plane along its axis. A cross-section is formed by cutting a solid (such as a cone, cylinder, or sphere) with a plane.
If a plane parallel cuts a cylinder-shaped item to its base, the resulting cross-section is a circle. As a result, the item has intersected. The object doesn’t need to be three-dimensional; this concept can equally be used for two-dimensional shapes.
You’ll also see some real-life cross-sections, such as a tree after it’s been chopped, which has a ring shape. We get a square by cutting a cubical box with a plane parallel to its base.
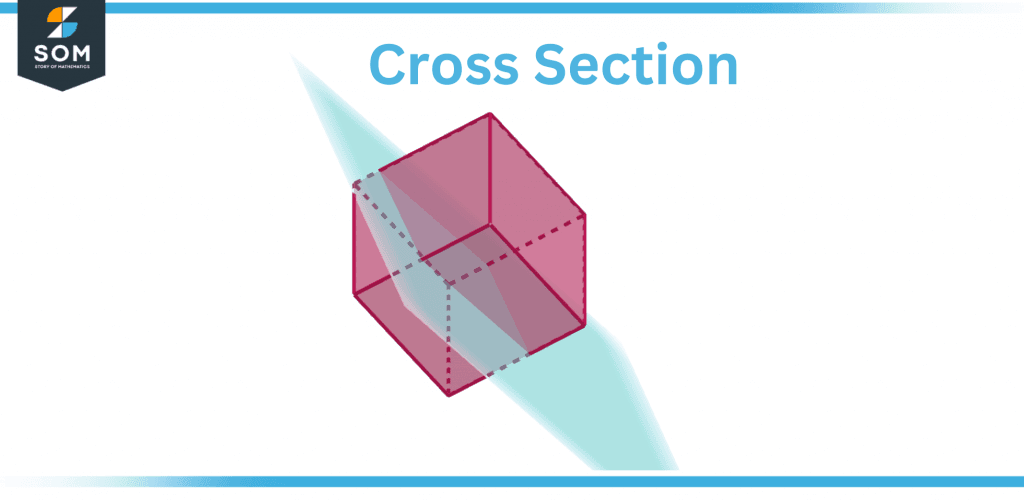
Figure 1 – Cross Section
Types of Cross Section
There are two main types of cross-sections
- Cross-section horizontal
- Vertical cross-section
Cross Section Horizontal
When a plane slices a solid object in the horizontal direction, it creates a parallel cross-section with the base, which is known as a horizontal cross-section. A cylinder’s horizontal cross-section, for example, is a circle.
Cross Section Vertical
A plane slices the solid shape in the vertical direction perpendicular to its base in a perpendicular cross-section. A cylinder’s vertical cross-section, for example, is a rectangle.
When three-dimensional shapes are cut in various ways, several types of cross-sections result. These can be tough to visualize at times. When a three-dimensional image is chopped parallel to its base, the shape of the base is obtained. For example, if a cylinder is sliced parallel to its base, the cross-section is a circle, much like the cylinder’s base.
Another example would be when cutting a square pyramid parallel to or horizontally to its base. Because the base is also a square, this cross-section would be a square.
Area of Cross-section
The the area of a two-dimensional shape obtained by slicing a three-dimensional object, such as a cylinder, perpendicular to some defined axis at a point is called cross-sectional area.
The cross-section of a cylinder, for example, is a circle. when sliced parallel to its base. As a result, the cross-sectional area of this slice is equal to the area of a circle having radius that is equal to the radius of the supplied cylinder.
Keep in mind how to determine a cylinder’s volume or prism by utilizing its cross-sectional area and length (height), The volume computation is simple if the cross-sectional area is known and constant along the height. But what if the cross-sectional area changes in a predictable way along the height line, as it does for a cone or pyramid, How could a single calculus approach be used to calculate the volume of either of these types of solids?
A circular cylinder can be formed by translating a circular disc along a perpendicular to the disc line. In other words, the cylinder can be formed by moving the cross-sectional area A (the disc) h distance. The resulting volume is known as the volume of the solid and is defined as V= A x h.
Cone Cross Sections
A cutting plane is a plane that forms a cross-section when it intersects a cone. A varied shape is generated depending on how the cutting plane crosses the cone. Any parallel cross-section of a circular cone generates a circle that is comparable (all circles are similar) to the base. This is valid for any parallel cone cross-section.
When a circular cone’s cutting plane is not parallel to its base, the cross-section will be an ellipse, parabola, or hyperbola. When the cutting plane to the opposing slant height line is parallel, a parabola is created.
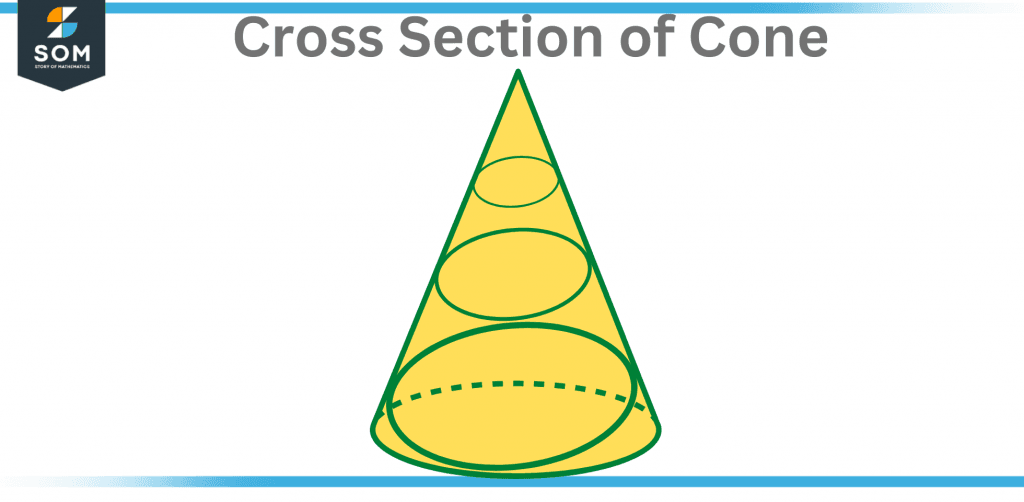
Figure 2 – Cross Section of Cone
Cylinder Cross Sections
A cylinder’s cross-section can be a circle, rectangle, or oval depending on how it was cut. The form obtained is a circle if the cylinder has a horizontal cross-section. If the plane slices the cylinder perpendicular to the base, the resulting shape is a rectangle. The oval shape is obtained by cutting the cylinder parallel to the base with a minor angle change.

Figure 3 – Cross Section of Cylinder
Sphere Cross Sections
A sphere’s cross-sections are two-dimensional figures created by the intersection of a plane with a sphere. Because the sphere has a perfectly round shape with a constant radius, every plane that meets a sphere will form a circular cross-section regardless of the plane’s inclination.
A sphere is a shape that has three dimensions, it is perfectly spherical and has a constant radius in all directions. This means that cutting a sphere with a plane will always result in a circular cross-section, regardless of the plane’s inclination.
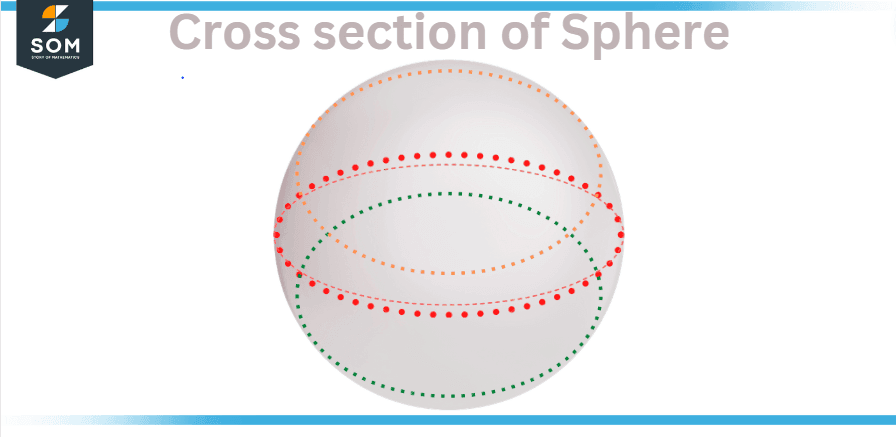
Figure 4 – Cross Section of Sphere
There are three types of cross-sections depending on the direction of the plane that cuts the sphere:
- Cross-section horizontal
- Vertical cross-section
- Inclined cross-section
However, as previously stated, all sphere cross-sections will be circular.
Examples of Cross Section Calculations
Example 1
what is the cross-sectional area of a plane that is perpendicular to a cube’s base with a volume of 64 cm$^3$.
Solution
As we already know:
Cube volume = Side$^3$
Therefore:
Side$^3$ = 64 [Given 4 cm on either side]
Because the cube’s cross-section is a square, the side of the square is 4 cm.
As a result, the cross-sectional area = a$\mathbf{^2}$ = 4$\mathbf{^2}$= 16 sq.cm.
Example 2
Determine the cross-section area of a cylinder with a height of 35cm and a radius of 8 cm?
Solution
Given:
4 cm radius
25 cm in height
We know that when a plane slices a cylinder parallel to the bottom, the resulting cross-section may be a circle.
As a result, the area of a circle, A, is equal to r$^2$ square units.
Take $\pi$ = 3.14, and change the values:
A = 3.14 (8)$^2$ cm2
A = 3.14 (64) cm$^2$
A = 200.96 cm$\mathbf{^2}$
The cylinder’s area is 200.96 cm$\mathbf{^2}$.
Example 3
A solid, metallic right circular cylindrical block with a height of 12 cm and a radius of 9 cm is melted, and little cubes with a 2 cm edge are formed from it. How many cubes may be formed from the block?
Solution
We have a radius (r) = 9 cm and height (h) = 12 cm for the correct circular cylinder.
As a result:
volume = $\pi$ x r$^2$ x h.
= 3.14 × 9$^2$ × 12 cm$^3$
= 3052.08 cm$^3$
All images/mathematical drawings were created with GeoGebra.
