JUMP TO TOPIC
Concave|Definition & Meaning
Definition
Concave is defined as a shape that has an inward curve. Any shape with an internal angle greater than 180° has a concave surface. It has the word “cave” that tells that a concave shape will be like the entrance of a cave.
For example, in a hexagon, if any two sides are curved inwards, then it is called a concave hexagon. Figure 1 shows a regular hexagon and a concave hexagon.
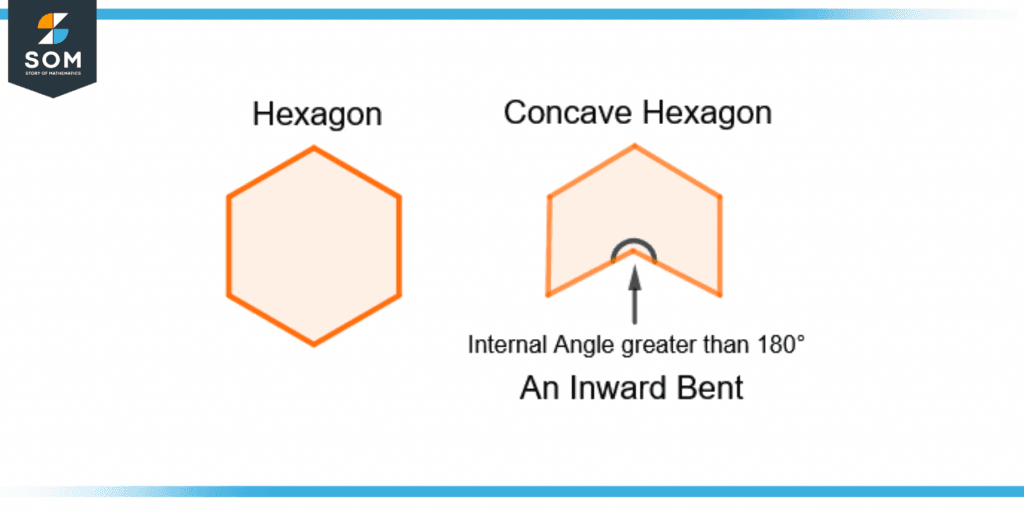
Figure 1 – A Regular Hexagon and a Concave Hexagon
Lens
A lens is defined as a transparent optical device that is used to refract light rays. They focus at a point to form an image of an object.
There are two types of lenses; simple and compound lenses.
A concave lens is a simple lens as it only consists of a single lens whereas a compound lens consists of more than one lens in its geometry.
Concave Lens
A concave lens has a thin middle area and is thicker in the outer edges. Figure 2 shows a concave lens.
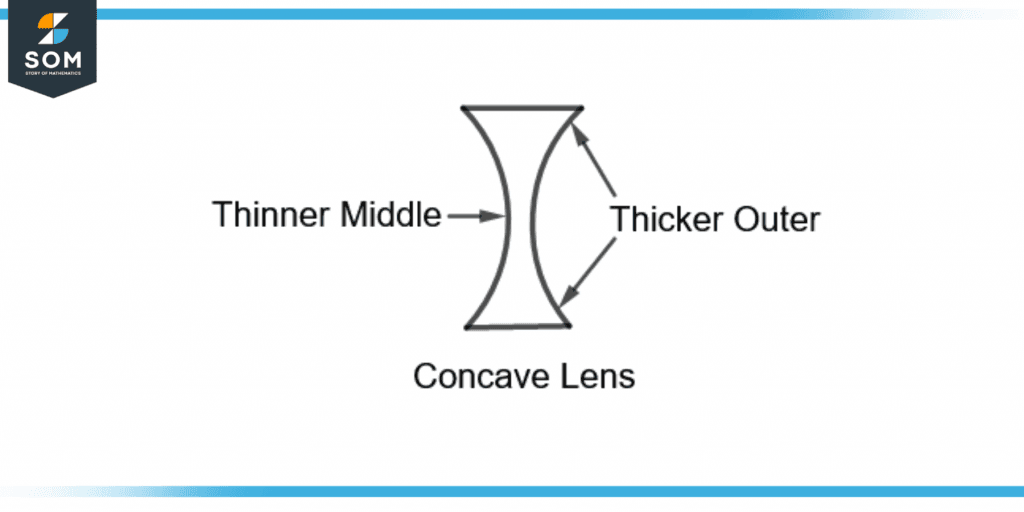
Figure 2 – A Concave Lens
It refracts light rays to disperse them in all directions. It has a variety of uses including the treatment of myopia that is shortsightedness.
A Diverging Lens
The concave lens is also known as the diverging lens. This is because it diverges the light rays that are refracted through it.
Figure 3 shows light rays passing through the concave lens.
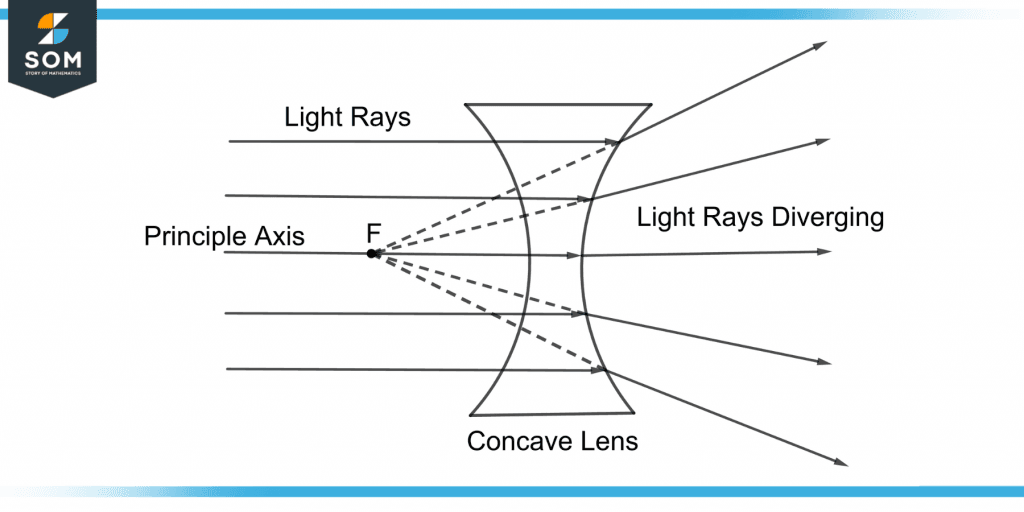
Figure 3 – Light Rays Diverging Through a Concave Lens
In figure 3, F is the concave lens’s focal point or focus. It is the point where all the light rays coincide when traced backward. Thus, the concave lens focuses the light rays at point F.
The principle axis is the axis that passes through the focal point and the optical center of the concave lens.
Image Formed by a Concave Lens
The image of the object formed by the concave lens is real or virtual(diminished) and erect(upright). Figure 4 shows a virtual image formed by a concave lens.
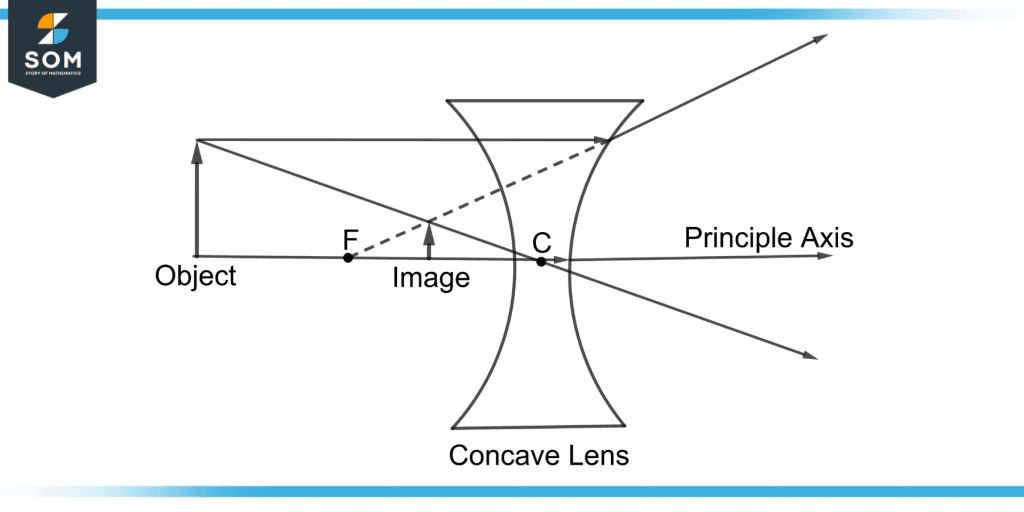
Figure 4 – A Virtual Upright Image Formed by a Concave Lens
The image is formed between the focal point F and the optical center C of the concave lens.
The image is upright and inward. It is also virtual or diminished, meaning the image appears smaller than the object’s size.
Focal Length of a Concave Lens
The distance from the center to the focal point F of a lens is called the focal length denoted by “f”.
It can be calculated by using the formula given below:
\[ \frac{1}{f} = \frac{1}{i} \ – \ \frac{1}{o} \]
Where i and o are the distances of the image and object respectively from the center of the lens.
Figure 5 shows the focal length, object distance, and image distance when light rays are refracted through the concave lens.
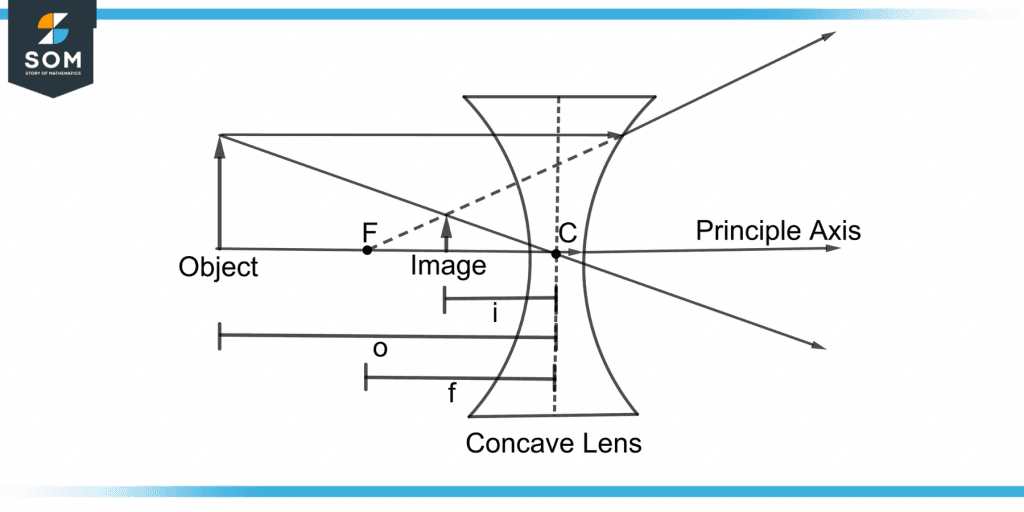
Figure 5 – Demonstration of Focal Length, Image and Object Distance of a Concave Lens
The concave lens’s focal length is always negative by sign convention. It is because the concave lens diverges the light rays. It is on the lens’s left side, which also makes it negative.
That is why it is also called a negative lens.
Magnification
Magnification is the ability to enlarge the object’s apparent size from its original size. It is calculated by using a ratio thus magnification has no units.
A magnification of one means that the object’s size and the image size are the same.
A magnification number greater than one means that the image is enlarged and a magnification less than one means that the image is diminished or de-magnified.
A concave lens always has a magnification of less than one. This is because the image formed is always smaller than the object’s size.
Magnification can be calculated by using the formula given below:
\[ m = \frac{ h_{i} }{ h_{o} } \]
Where,
$h_i$ = height of the image
$h_o$ = height of the object.
Height is the vertical distance. Another formula for magnification is:
\[ m = \frac{i}{o} \]
Where i is the image distance and o is the object distance.
Applications
There are many applications of concave lenses one of which the most common are eyeglasses for myopia correction.
The eyeball with myopia is elongated which can’t focus light from far away objects. The concave lens diverges the light rays coming to the eyeball which helps it make a clearer image of distant objects.
Concave lenses are also used in binoculars, compound microscopes, cameras, spy holes, mobile phones, telescopes, and flashlights.
Types of Concave Lens
Different variations and additions to concave lenses produce the following types.
Plano-concave Lens
A Plano-concave lens has a plane surface on one side and a concave surface on the other. It has a negative focal length like the concave lens.
Biconcave Lens
A biconcave lens is a compound lens and has two concave lenses joined together. Both lenses have the same optical center.
Convexo-concave Lens
A Convexo-concave lens has one concave surface and one convex surface. The concave side is more curved as compared to the convex side.
Figure 6 shows these three lenses.
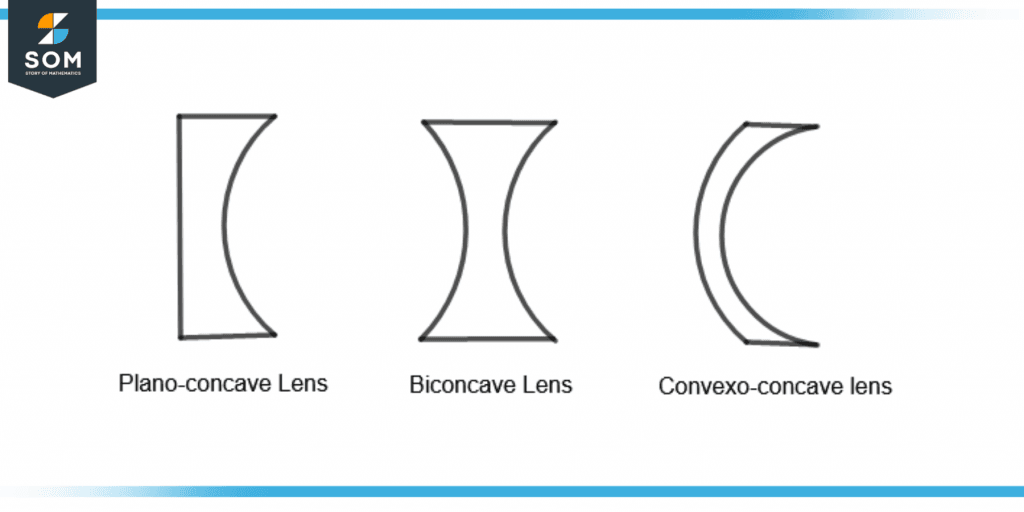
Figure 6 – Types of Concave Lens
A Solved Problem Involving a Concave Lens
A concave lens forms an image at 7 cm from the optical center. It has a focal length of 14 cm. Find the distance of the object from the lens. Also, calculate the magnification.
Solution
The formula for focal length is:
\[ \frac{1}{f} = \frac{1}{i} \ – \ \frac{1}{o} \]
The focal length and the image distance of a concave lens will be negative as it is on the left of the lens. So, the given values are:
f = -14 cm , i = -7 cm
Calculating the object distance o, the formula becomes:
\[ \frac{1}{o} = \frac{1}{i} \ – \ \frac{1}{f} \]
Putting the values gives:
\[ \frac{1}{o} = \frac{1}{-7} \ – \ \frac{1}{-14} \]
\[ \frac{1}{o} = – \frac{1}{7} + \frac{1}{14} \]
\[ \frac{1}{o} = \frac{ – 2 + 1 }{14} \]
\[ \frac{1}{o} = \frac{ -1 }{14} \]
\[ o = – \ 14 \]
So, the object distance is 14 cm. The negative sign indicates that the image formed was virtual.
The magnification is calculated as follows:
\[ m = \frac{i}{o} \]
\[ m = \frac{-7}{-14} \]
\[ m = \frac{1}{2} \]
So, the magnification is 0.5.
All the images are created using GeoGebra.
