JUMP TO TOPIC
Circle|Definition & Meaning
Definition
A circle is a closed, two-dimensional rounded object in geometry. As its name implies, a circle has no sharp or sharply rounded corners or edges. A car tire and a wall clock are some examples of various ordinary objects with circular shapes.
The Core or Center of a Circle
The point in the middle of a circle from where the distance of all points on the circle’s boundary or circumference is the same is called the circle’s core or center. This length of distance is referred to as the circle’s radius.
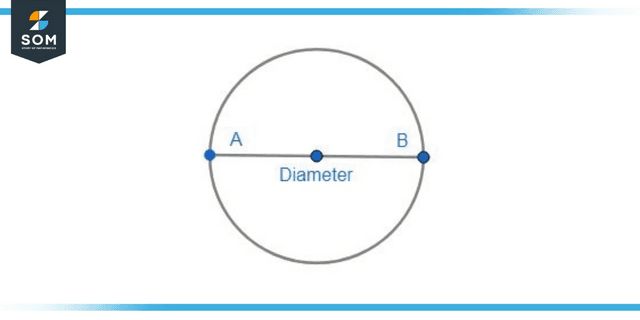
Figure 1: Diameter of a circle. It passes through the center.
Interior and Exterior of the Circle
Consider the circle with P as its center and r as its radius. A circle can be divided into two distinct regions: the interior and the exterior.
The portion of a circle containing all of the points whose distances from the center are shorter than the circle’s radius is called the interior or inside of the circle. The portion where every point’s distance from the center is greater than the radius is called the exterior or outside of the circle.
The circumference is the boundary of a circle that encompasses all points whose distances are exactly equal to the circle’s radius. This set of points is said to reside “on the circle.”
Parts of a Circle
A Circle’s Radius
The radius is a line segment that passes through the circle’s center and ends on the circle itself.
The formula for finding the radius is given:
Radius = Diameter/2
Diameter of Circle
The diameter of a circle is a line segment that joins two ends of the circle’s boundary while passing through the center of the circle. Essentially, if you extend the radial line until it touches the circle’s boundary, you get the diameter. The formula for diameter:
Diameter = 2 x Radius
Circumference of Circle
Simply put, the circumference of a circle is the distance along the circle’s perimeter. That number is equivalent to the perimeter of any other form.
Circle Chords
The chord of a circle is a segment of a line with both of its endpoints on the circle. The most significant chord of a circle is called its diameter. The diameter is simply a chord that passes through the circle’s center.
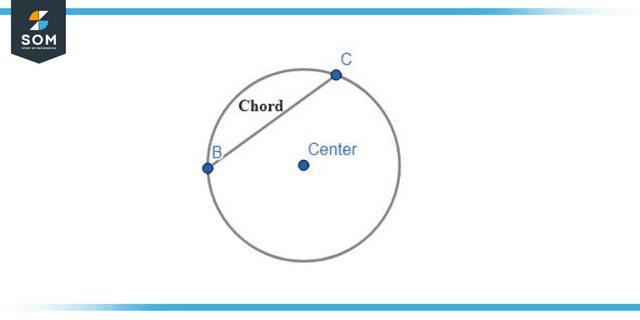
Figure 2: Chord of a circle
Arc of a Circular Segment
The arc is a part of the circle’s boundary, so the length of an arc is smaller than the circumference. It is characterized by two vertices on the circle’s boundary and follows the same curvature as the circle. A semicircle is basically an arc with a degree measure of 180 degrees that connects the poles of the diameter.
A circle can be split into two arcs. Minor arcs are the smaller ones (in length), while major arcs are the larger ones.
Circle’s Secant
A secant is a line that cuts across the center of a circle in two distinct places.
Circle’s Tangent
A tangent is defined as a line that meets a circle in one and only one location.
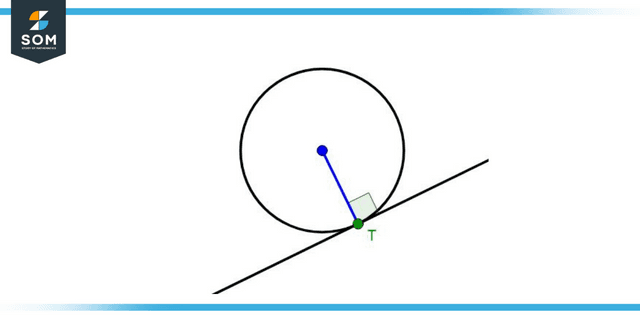
Figure 2: Tangent of a circle, cutting it at point T only.
Segments of a Circle
The circular region is cut in half along the chord of the circle. The term “segment” refers to each section of the cut circle. The difference between a segment and an arc is that an arc consists only of the circle’s boundary, while a segment contains both the arc and the chord joining the arc’s vertices. As such, the arc only has a length while the segment covers an area.
Small segments are those that contain a minor arc, whereas major segments are those that feature a significant major arc.
The Circular Sector
A circular sector consists of any two radii and the arc between them, whose vertices are the intersections of the radii with the circle’s boundary.
Two sectors are formed from two radii meeting in the middle of a circle. If the circle’s minor arc forms a portion of the sector’s boundary, we refer to that sector as the minor sector. The primary sector is the one that includes the main arc of the circle.
Portions of a Circle
Semicircle: Since “semi” implies “half,” a semicircle is simply half of a circle. It is produced by splitting through the center of a complete circle using a line that runs along its circumference. The term “diameter” refers to the length of this particular line segment.
Quarter Circle: One-fourth of a whole circle is a quarter. One can create a quarter circle by dividing a whole circle into four equal sections or a semicircle into two halves. For instance, A quadrant is a quarter circle.
Area of a Circle
When viewed in a two-dimensional plane, the space that is taken up by a circle is referred to as its area. Alternately, one may refer to the space occupied within the perimeter or circumference of a circle as the area of the circle.
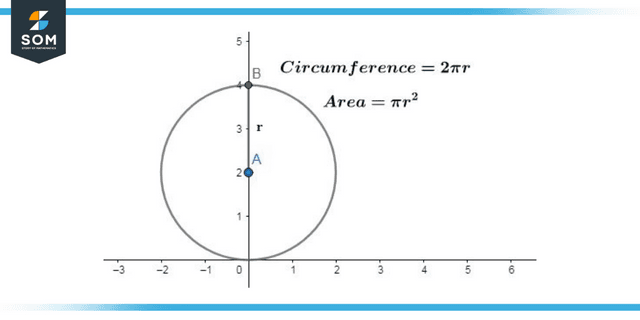
Figure 4: Area and Circumference of a Circle
The formula for calculating the area of a circle is A = πr², where r is the circle’s radius, and π, pronounced “pi,” is a mathematical constant depicting the ratio of a circle’s circumference to its diameter. It is an irrational number, so its value is approximated by 22/7 or 3.14. The square unit is the standard for measuring area; this includes m², cm², and so on.
You can calculate the size of a circular field or plot with the help of the area of a circle formula. Assuming you have a round table, we can use the area calculation to determine how much fabric is required to cover it. We may calculate the circle’s boundary length or diameter using the area formula. You can’t measure the volume of a circle since it doesn’t exist. A circle is a flat, non-volume-containing shape. The only measurements of a circle are its area and circumference.
Example Problems Involving Circles
Example 1
Find the area and circumference of the circle with r = 4, and also define the chord.
Solution
Since the radius of the circle is four, the diameter will be eight. It is because radius is half of diameter. Therefore:
A= πr²
= π(4)² = π.16
= (22/7).16 = 50.2 cm² or m²
Circumference or S = 2πr = 2(22/7)(4)
S = 25.142 cm or m
The chord is a segmented line between two points on a circle’s curve. It should be noted that the radius of the circle is not a chord.
Example 2
A distance of 10km is covered by the wheel, rotating 6,000 times, find the radius of the wheel?
Solution
Let the circumference be S, then S=2πr. A rotation is the circumference of the wheel. Therefore:
10/6000 = 0.00166km
0.00166km is the distance covered in one rotation, and thus, is the circumference of the circle.
S= 2πr
r= S/2π
r= 0.00166/2π
r = 0.000264km or 26.4cm
It should be noted that one whole circle forms circumference; therefore, one whole rotation is same as the entire circle’s boundary.
All images/graphs are created using GeoGebra.
