Byte|Definition & Meaning

Introduction to Byte 

A byte is used for basic information that we see on a computer nowadays whether it is an image or a machine code. A byte consists of a set number of bits that are used for various application purposes.  

A byte can be represented by either 0s or 1s. Here 0 represents the OFF state and 1 represents the ON state within a computer system. Every combination of bits is used to represent different sorts of data for example 8 bits are equal to 1 byte and 4 bytes are equal to 1 word. 

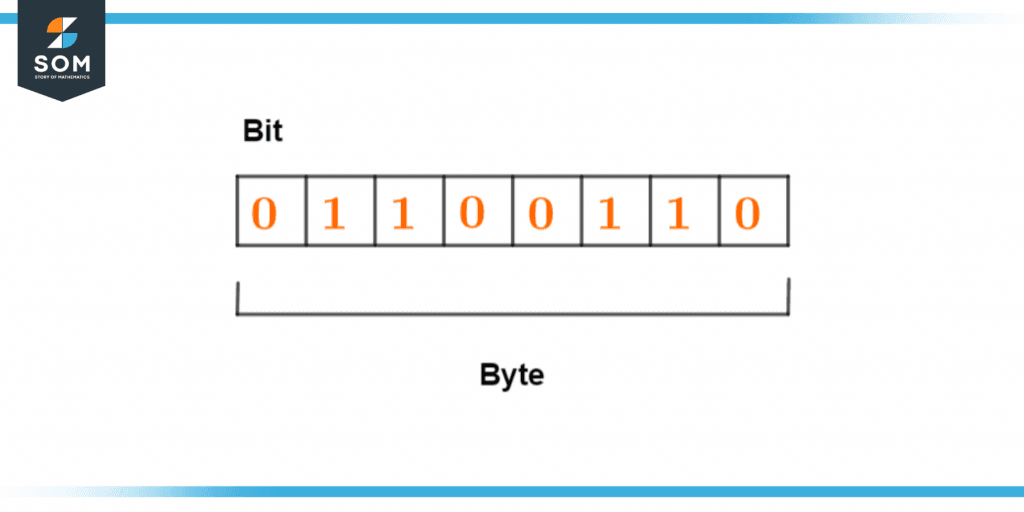
Figure 1 – 8 bits form 1 byte

Computer processors vary from each other due to their capability of handling two-byte or single-byte instructions. Two-byte instructions are also known as double-byte characters.

Detailed Discussion

We represent byte with a capital B whereas bits are represented with a small b. An 8-bit byte can be used to represent 256 characters. Commonly the size of a single byte is 8 bits but it is not fixed. To represent larger amounts of data we use prefixes to help us out. Each prefix represents a different set of values for both bytes and bits. As we know that bits are used to represent bytes and bytes are used to represent computer storage. 

These Byte multiples can be measured by using these 2 systems:

1. Base-2
2. Base-10

We use the base 10 system which is also known as the decimal system consisting of numbers from 0 to 9. But computers can not understand this format so we convert our number system into a base 2 number system which is also known as a binary number system. A binary number system only consists of two numbers which are 0 and 1.

For bytes, the following are the common prefixes that we use:

1. A Kilobyte(KB) is equal to 1024 Byte 
2. A Megabyte(MB) is equal to 1024KB or 1,048,576 Bytes
3. A Gigabyte(GB) is equal to 1024MB or 1,073,741,824 bytes
4. A Terabyte(TB) is equal to 1024GB or 1,000,000,000,000 bytes

We can convert our data according to the need of the user. 

In a computer, the data is stored in the form of an array which consists of bits carrying the information to and from the CPU. the data is stored in these arrays in such a manner that goes from right to left. Each block has its value according to which the data is dealt with. The bit that is to the extreme left is known as the most significant bit (MSB) and the bit to the extreme right is known as the least significant bit (LSB).

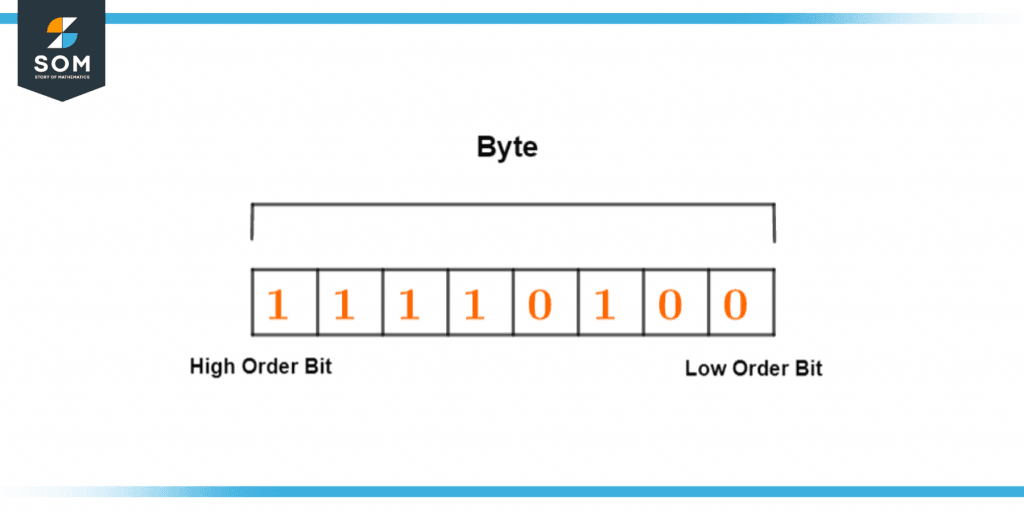
Figure 2 – Each byte has a least and most significant bit

Base-10 to Base-2 Conversion

Let us take a look at the following image:

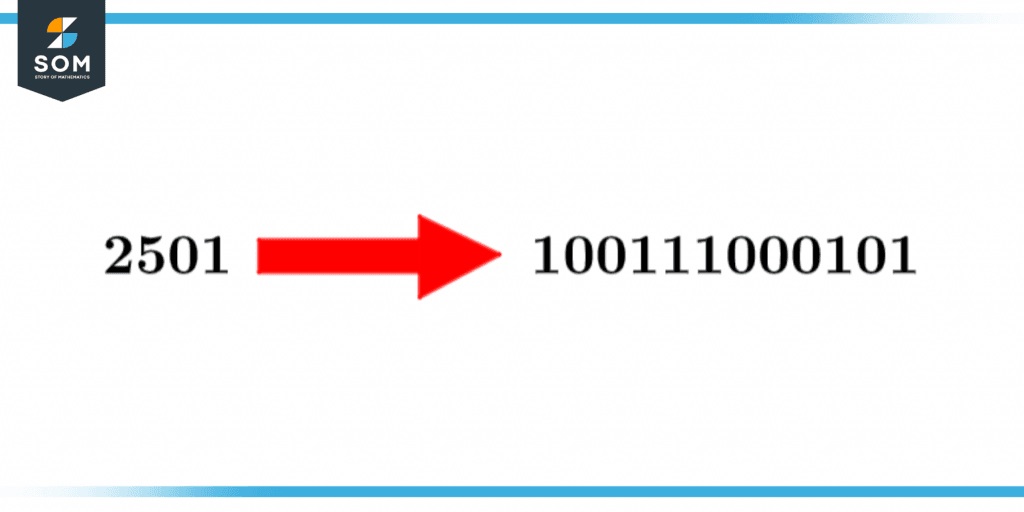
Figure 3 – Conversion of a number into its binary form

This image shows the conversion of a base 10 number into a base 2, which in other words is known as a decimal to binary conversion. This is a process that helps the computer system understand any command given by the user. As a computer can only understand binary languages based on 0s and 1s we need to understand this concept too.

For a decimal-to-binary conversion, we will use the following steps:

Step 1: We will divide the given number by 2 and will note the remainder.

Step 2: The quotient of the previous division will be used now. We will follow the same division method and will divide the quotient with 2 and will note the remainder.

Step 3: We will repeat this process until we get 0 as the quotient. 

Step 4: Now write all the remainders together in such a manner that the last remainder comes first and the rest follow accordingly in a reverse form.

Visual Description

Bytes are used in the form of multiples according to the need of the computer. Its memory hierarchy is as given below:

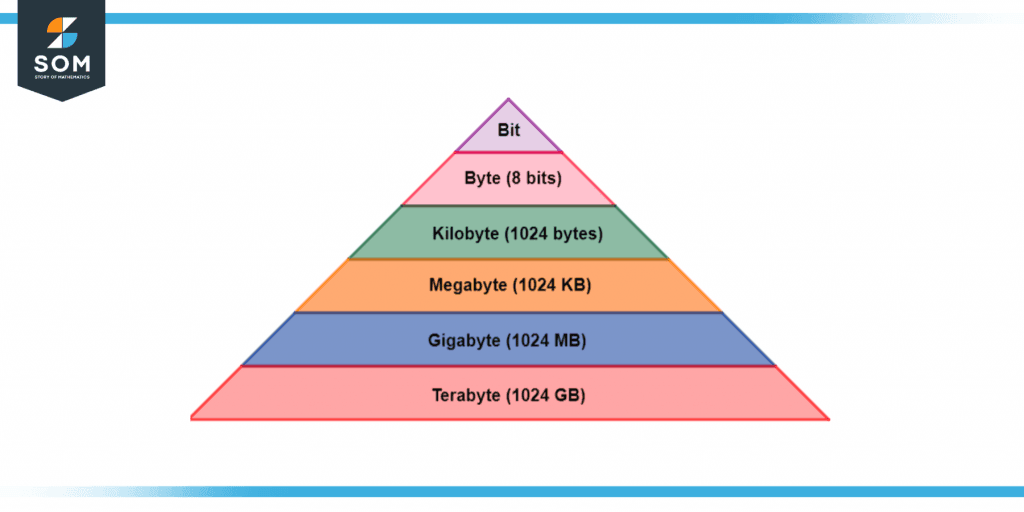
Figure 4 – Memory Hierarchy in the form of bytes

Here bit is the smallest addressable memory unit whereas terabyte is the largest memory unit. For a memory unit greater than a bit and smaller than a byte we use a nibble. A nibble is the combination of 4 bits. 

To form a word we require 4 bytes. This is the minimum requirement for a computer to form a word. We can see it in the following figure:

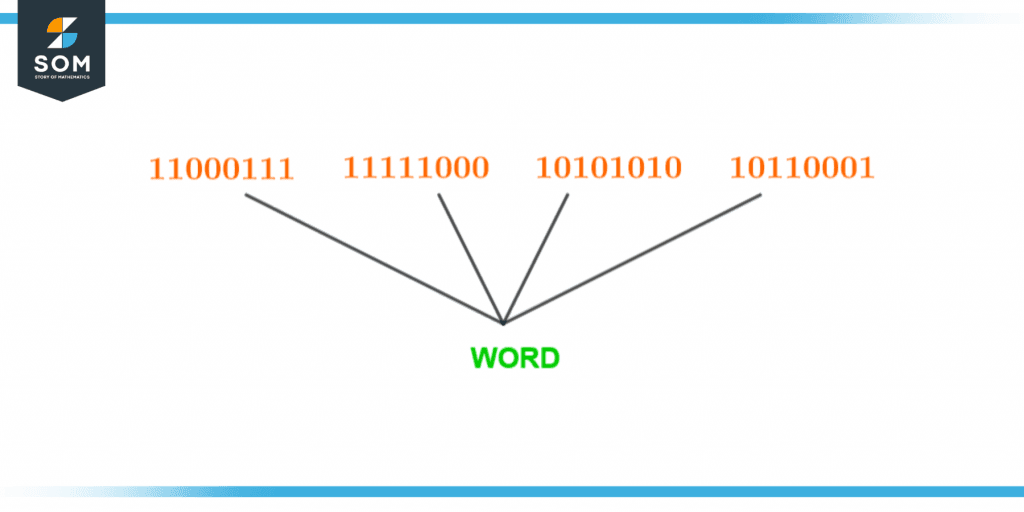
Figure 5 – Formation of a word using bytes

Solved Examples of Byte

Example 1

David wants to convert 25 GB of the data files into Kilobyte (KB). Help him in this conversion.

Solution

As we know that in a computer the memory hierarchy is:

1. A Byte (B) is equal to 8 bits
2. A Kilobyte (KB) is equal to 1024 Byte 
3. A Megabyte (MB) is equal to 1024KB or 1,048,576 Bytes
4. A Gigabyte (GB) is equal to 1024MB or 1,073,741,824 bytes
5. A Terabyte (TB) is equal to 1024GB or 1,000,000,000,000 bytes

Now to convert GB into KB, we are going to climb up the memory pyramid. For that, we proceed as follows.

As we know, a gigabyte is 1024 MB which is 1024 KB, so we will multiply the value given by 1,000,000. So the formula that we can use here is

KB = 1,000,000 * GB

Now putting the values:

KB = 1,000,000 * 25

KB = 25,000,000

So 25 GB is equal to 25,000,000 KB.

Example 2

State how many possible combinations can come from 8 bits or 1 byte.

Solution

To find all possible combinations we are going to use the base 2 technique. In this method, we are going to use the number 2 as the base and each number will have its exponential value based on its position starting from right to left. Then we will add them all together to get our answer. The following steps explain the method:

A = 2^7 + 2^6 + 2^5 + 2^4 + 2^3 + 2^2 + 2^1 + 2^0

We will always start from 0 and not 1. Now taking the power, we get:

A = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1

Now adding these values we get:

A = 255

Therefore the total decimal values that you get are 255.

But in the decimal number system, the number 0 is of no value whereas in binary 0 holds a value so the number of combinations will be after adding the value of zero is:

255 + 1 = 256

Images/mathematical drawings are created with GeoGebra.

Brackets Definition < Glossary Index > Cancel Definition