- Home
- >
- Fundamental counting principle – Explanation & Examples
JUMP TO TOPIC
Fundamental Counting Principle – Explanation & Examples
The fundamental counting principle is a mathematical rule that is extensively applied in the evaluation total number of possible arrangements of a set of objects. These calculations are essential for solving many probability problems.
The fundamental counting principle states that if one event can occur in $A$ different ways and a second event can occur in $B$ different ways, then the total number of ways in which both events can occur is $A \times B$.
After reading this article, you should understand:
- The Fundamental Counting Principle
- Difference Between the Rule of Sum and the Counting principle
- Examples of the Fundamental Counting Principle
- Applications of the Counting principle
It is advisable to refresh the set theory to better understand the material discussed in this article.
What is the Fundamental Counting Principle
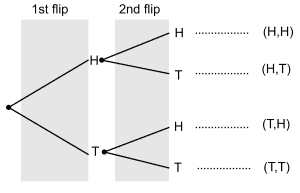
Let us consider the example of flipping a fair coin twice. When the coin is tossed the first time, we either get Heads or Tails, and the sample space can be written as $S = \{H, T\}$. When the coin is tossed the second time, the sample space we get is $S = \{HH, HT, TH, TT\}$. The first flip can result in two different outcomes, and so does the second flip. So, the total number of possible outcomes is $2 \times 2 =4$. The example is illustrated in the form of a tree diagram below:
Let us take another simple example, James has to go to a party, and he has three different shirts and two different pants to choose from. The shirts are red, black and white in color while the pants are blue and green in color. How many possible outfits can James choose from? James can wear either of the two pants with each shirt.
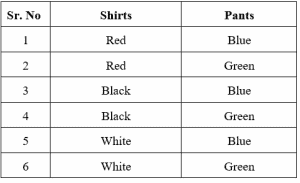
So, James can wear Red shirt with either Blue or Green pants. Similarly, Black and White shirts can be selected with either Blue or Green pants. As the table shows, there are six numbers of possible outfits. We can calculate it easily through the rule of counting principle. We had 3 different options for shirts and two different options for pants so, $3 \times 2=6$ possible outfits.
Fundamental Counting Principle definition
If there are $A$ different ways of selecting an object and $B$ different ways of selecting another object, then the total number of possible ways for selecting both objects together is $A\times B$.
Example 1: Harry went to a food restaurant, and he wants to order a combo deal that includes a pizza, drink, and dessert. The following choices are available:
Pizza: Chicken Fajita and Vegetable
Drink: Pepsi and 7-Up
Dessert: Ice-cream and Pie
Solution:
We are given three different objects to choose from. There are three different types of pizza, four different types of drinks, and three different types of dessert. Let us draw a tree diagram.
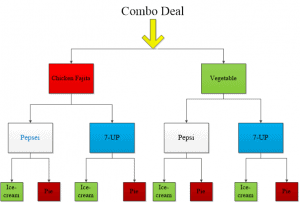
As the tree diagram shows, we can work out the possible arrangements for a combo deal.
Deal 1: Chicken fajita, Pepsi, and Ice-cream
Deal 2: Chicken fajita, Pepsi, and Pie
Deal 3: Chicken fajita, 7-UP, and Ice-cream
Deal 4: Chicken fajita, 7-UP, and Pie
Deal 5: Vegetable Pizza, Pepsi, and Ice-cream
Deal 6: Vegetable Pizza, Pepsi, and Pie
Deal 7: Vegetable Pizza, 7-UP and Ice-cream
Deal 8: Vegetable Pizza, 7-UP and Pie
Now solving it by counting principle, we have 2 options for pizza, 2 for drinks and 2 for desserts so, the total number of possible combo deals $= 2 \times 2 \times 2 =8$.
Example 2: Steve has to dress for a presentation. He has $3$ different shirts,$ 2$ different pants, and$ 3 $ different shoes available in his closet. Wearing the Tie is optional. Calculate the total number of possible outfits.
Solution:
There are three types of shirts, two types of pants and three types of shoes. While the tie is optional, the tie has two options, either “Yes” or “No.”
Total number of possible outfits $ = 3 \times 2 \times 3 \times 2= 36$.
The Rule of Sum
The rule of sum states that if event $A$ can occur in $n$ different ways and event $B$ can occur in $m$ different ways. In contrast, both events $A$ and $B$ are mutually exclusive, then the total number of possible outcomes can be given as $n + m$. So, unlike the counting principle, we add both the events; however, it must be remembered that the condition for the rule of the sum is that the events must be mutually exclusive.
Example 3: Jessica has a jar of cookies. It has $3$ chocolate and $3$ peanut cookies in it. Jessica only wants to eat one cookie. How many possible options does Jessica have?
Solution:
Since Jessica only wants one cookie, she has to choose only one cookie from 3 chocolate or 3 peanut cookies. The choices are mutually exclusives, so by applying the rule of sum, we have $3+3= 6$ possible options.
Example 4: Ellie went to a dress shop to purchase a single blue dress. The shop has $14$ plain blue dresses, $13$ plain red dresses, 10 blue embroidered dresses, and $5$ red embroidered dresses. How many options does Ellie have?
Solution:
Since Ellie wants to choose a blue dress so, we will eliminate all red dresses. She can choose from 14 plain blue dresses or 10 blue embroidered dresses. So, the total numbers of option are $14+10 = 24$
The Counting Principle and Rule of Sum
We have discussed the problems related to the fundamental counting principle and the rule of sum. What if a problem has to be solved using both the rules? Let us discuss a few examples.
Example 5: Harris went to a shop to buy some items of clothing. He can choose a shirt from 3 different colors or a T-shirt from 2 different colors. Also, he can either get a pair of pants from 3 available colors or a pair of jeans from three available colors. How many possible outfits can Harris have?
Solution:
Harris can take one shirt from the given 3 colors or T-shirts from the available 2 colors. So number of available shirts $= 3+2 =5$.
Similarly, he can choose a pair of pants from either 3 options or a pair of jeans from three options. The number of available pairs of jeans/pants $3+3=6$.
So, we have $5$ different shirts and $6$ different pants, and the total number of possible outfits will be $5 \times 6= 30$.
Example 6: Steve wants to go to a job interview in another city. He can choose from $4$ local bus services or $3$ taxi services to reach the other city. From there, he can choose from $3$ local bus services or $2$ taxi services to reach the place of his interview. How many possible routes/ways Steve can travel to his destination?
Solution:
Steve can choose to take either a local bus or a taxi to reach the other city. So, the possible numbers of vehicles that can be used to reach the city are $4+3 =7$. Similarly, Steve can either choose from $3$ local bus services or $2$ taxi services to reach the location of the interview from the city. Number of possible option $3+2=5$. Now, the total number of ways/vehicles Steve can use to reach his interview destination is $7 \times 5 = 35$.
Fundamental Counting Principle formula
The basic formula for the fundamental counting principle is the same as its definition, i.e., if we have $A$ ways/options to do task-1 and $B$ ways to do task-2, then the total number of ways we can do task-1 and task-2 together are $A \times B$.
However, by applying the fundamental counting principle in questions related to possible arrangements of a given set of objects, we can derive formulae for permutations and combinations as discussed below:
Applications of the Counting Principle
Suppose $5$ boys $\textrm{A, B, C, D, and E}$ are to be seated on a couch in a row. Then in how many possible ways can they be seated? Suppose that $\textrm{Boy A} = \textrm{event A}$, $\textrm{Boy B} = \textrm{event B}$ and so on. So, for event $A$, we have five possible options, for the event $B$, we have four possible options, for the event $C$, we have three possible options, for the event $D$, we have two possible options and one option for the event $E$.
By the rule of counting principle to calculate the total number of ways, we multiply the possibilities of each event. In this case the total number of possible outcomes is $5 \times 4 \times 3 \times 2 \times 1= 120$. This is also known as permutation, and it is an application of the counting principle.
Permutation
A permutation of $n$ different objects taken $r$ at a time where $r ≤ n$, then the arrangement of r objects can be represented by
$ P(n,r) = \frac{n!}{(n-r)!} $
Where $n! = n\times(n-1)\times(n-2)…..\times1$.
Example 7: Calculate the number of ways in which digits from $0-9$ can be arranged.
Solution:
There are total numbers of $10$ digits. The number of ways in which the first digits can be arranged is 10. Similarly, for the second digit, we have 9 available options and so on for the rest of the digits. The total numbers of possible ways to arrange the digits
$10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800$.
Example 8: Calculate the number of ways in which four digits can be selected from $0-9$.
Solution:
There are total numbers of 10 digits, and we have to select only four from the available 10 digits. Here $n = 10$ while $r = 4$.
$ P(n,r) = \frac{n!}{(n-r)!} $
$ P(n,r) = \frac{10!}{(10-4)!} $
$ P(n,r) = \frac{10!}{6!} $
$ P(n,r) = \frac{2628800}{720} $
$ P(n,r) = 5040 $.
Just Like permutation, the combination is also an application of the counting principle.
Combination
The combination is a process of selecting objects from a set without giving importance to the order of arrangement. For instance, let’s suppose we have a class of four students; let’s call them $A$, $B$, $C$, and $D$. We wish to make a team of three students. How many different teams can we make?
In this case, note that the team $\{A,B,C\}$ is the same as the team $\{A,C,B\}$ or $\{B,A,C\}$. In other words, the order in which the team members are selected does not matter. Such arrangements in which order does not matter are called Combinations. We can use the fundamental counting principle to come up with a formula for finding the total number of combinations.
For instance, in the example discussed above, if we assume that order does matter, then as discussed in the previous section, by the counting principle, we will have $4 \times 3 \times 2 \times 1$ possible arrangements. Now for any given arrangement, let’s say $\{A, B, C\}$, there are many possibilities such as $\{A, C, B\}$ or $\{B, A, C\}$ that result in the same combination. So, we need to figure out the total number of possibilities for any given arrangement that leads to the same team.
Since we have three slots and three members (i.e., $A$, $B$, $C$), so we can fill the first slot in three different ways, the second slot in 2 different ways, and the third slot in one different way. By the fundamental counting principle, we will have $3 \times 2 \times 1$ possibilities that lead to the same combination.
So the total number of unique combinations would be
$\large{\frac{4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}}$
Generally, if we have $n$ objects and we choose $r$ objects to make a combination, the total number of combinations is denoted by $C(n,r)$ and is given as
$C(n,r) = \frac{n \times n-1 \times n-2 \times \cdots n-r}{r \times r-1 \times r-2 \times \cdots 1}$
Multiplying both numerator and denominator by $(n-r)!$ and using the factorial rule, we can simplify the formula as
$C(n,r) = \frac{n!}{r!(n-r)!}$
Example 9:
A locker is locked with a four-digit password. The password only contains numbers from $0-6$. How many different password options will you have if the order of numbers does that matter?
Solution:
We have seven numbers to choose from and we have to make a $4$ digit password, hence $n=7$ and $r=4$, in this case. The total number of combinations is given as
$C(7,4) = \frac{7!}{4!(7-4)!}$
$C(7,4) = \frac{7 \times 6 \times 5 \times 4!}{4!3!}$
$C(7,4) = \frac{7 \times 6 \times 5}{3!} = 35$
Practice Question:
1. We have a group of four people; let’s call those Jhon, Jill, Liz, and Tom. We wish to make the team consisting of three people using the available group. However, Liz must be included in every team. How many distinct teams can we make?
2. Kevin wants to buy a new Honda car. The car is available in 4 different models, and every model has 5 different colors. Calculate the total amount of choices.
3. A coin is flipped 3 times. Draw a tree diagram and calculate the total amount of possible outcomes using the counting principle
4. Freya went to an ice cream shop. The menu has 2 cones available Large and Small, and both the cones are available in 3 different shapes. Flavors available for large cones are Vanilla, Mango, Chocolate, and Strawberry, while small cones also include all the flavors except Mango. How many choices does Freya have?
5.A restaurant has 6 different Appetizers, 5 different desserts, and 7 different meal options. Calculate the total number of options for given deals
a) Deal 1: It includes Appetizers and a meal.
b) Deal 2: Desserts and a meal.
c) Deal 3: Appetizers, a meal, and desserts.
Answer Key
1. 3
2. The car is available in 4 different models and 5 different colors. So, by the rule of counting principle total number of choices are $ 4\times5 = 20$.
3.
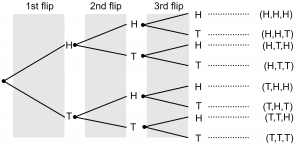
The first flip results in $2$ possible outcomes, so do the second and the third flip. Hence by the counting principle, the total possible outcomes will be $2 \times 2 \times 2 = 8$, which is also confirmed by the tree diagram.
4.
Freya has two different cones available large and small, which are mutually exclusives and cannot happen together. So, we will calculate possible outcomes for each and then add them up.
Total number of options for large cone ice-cream: $ 3\times4= 12$
Total number of options for small cone ice-cream: $ 3\times3 = 9$
Total number of possible options: $ 12+9 = 21$
5.
a) Total number of options for deal 1 : $ 6\times7 = 42$.
b) Total number of options for deal 2: $ 5\times7= 35$.
c) Total number of options for deal 3: $ 6\times7\times5 = 210$.
