What Is 3/25 as a Decimal + Solution With Free Steps
The fraction 4/7 as a decimal is equal to 0.571.
Division, out of all the mathematical operations seems to be the most complicated one. But it doesn’t have to be, as there is a way to solve this seemingly difficult problem. The method in question for solving fractions is called Long Division.
Here, we will solve the given fraction i.e., 4/7 using the Long Division as it will produce the decimal equivalent for this fraction.
Solution
We begin by first separating the constituents of the fraction based on the nature of their operation. The numerator in a fraction in the case of a division is called the Dividend, whereas the denominator is referred to as the Divisor. And this brings us to this result:
Dividend = 4
Divisor = 7
Now, we carry on by rearranging this fraction in a more descriptive fashion, where we also introduce the term Quotient which corresponds to the solution of a division:
\[ Quotient = Dividend \div Divisor = 4 \div 7 \]
Now, we can solve the problem as follows using Long Division:
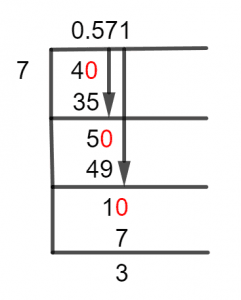
Figure 1
4/7 Long Division Method
The Long Division Method used to solve this problem can be further looked into as follows.
We had:
\[ 4 \div 7 \]
As we know, $7$ is greater than $4$, and therefore you can’t solve this division without introducing a Decimal Point. Now to introduce said decimal point, we plug in a zero to the right of our Remainder.
Now Remainder is another division-specific term used for the remaining value resulting from an incomplete division.
As in this case, $4$ is a remainder, we will introduce the Zero to its right, therefore turning it into $40$ in the process. Now, we solve for:
\[ 40 \div 7 \approx 5\]
\[ Where, \phantom {()} 7 \times 5 = 35 \]
This means that there is a Remainder produced from this division as well, and it is equal to $40 – 35 = 5$.
Having produced a remainder from the Division, we repeat the process and plug a zero to the Remainder’s Right. In this case, we don’t have to use another decimal point given that the Quotient is already a decimal value now.
The resulting remainder was $ 5 $, so addition of a Zero to its right will produce $ 50 $. Now we can move forward and calculate:
\[ 50 \div 7 \approx 7 \]
\[ Where, \phantom {()} 7 \times 7 = 49 \]
Thus, we have another Remainder equal to $1$. Bringing in another zero will produce $10$, thus in order to solve up to three decimal places we must calculate:
\[ 10 \div 7 \approx 1 \]
\[ Where, \phantom {()} 7 \times 1 = 7 \]
Thus, we have a Quotient equal to $0.571$ with a Remainder of $3$. This means that if we solve further, we may be able to get a more accurate result.
Images/mathematical drawings are created with GeoGebra.
