What Is 4/11 as a Decimal + Solution With Free Steps
The fraction 4/11 as a decimal is equal to 0.3636363636.Fractions are represented in p/q form, where the p in the fraction is known as the numerator, while q in the fraction is known as the denominator. These are separated by a line which is known as the division line. We can convert the fraction into a decimal value to make it more convenient and easy to understand, but for that, we have to use some technique or method. The method we prefer the most to convert fractions into their decimal value is the long division method.So we will solve the given fraction of 4/11 by the long division method to get its decimal value.
Solution
The Dividend and the Divisor are two important terms used in the long division method. The numerator in the fraction is called a “dividend,” while the denominator of the fraction is known as a “divisor.” So for the given fraction, we have a dividend of 4 and the divisor is 11.
Dividend = 4
Divisor = 11
Before showing the result through the long division method, there is a need to introduce a new term which is the result of the fraction in decimal form, and this term is referred to as the Quotient.
Quotient = Dividend $ \div $ Divisor = 11 $ \div $ 4
The long division method for the given fraction of 4/11 is as under: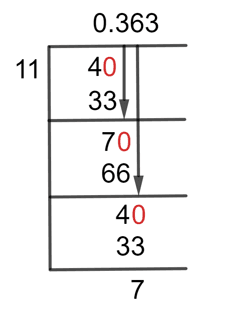
Figure 1
4/11 Long Division Method
Let us the long division method to solve the fraction step-by-step as follows:
4 $ \div $ 11
We cannot divide the two values directly because the numerator is less than the denominator, so we will introduce a decimal point in the quotient. By doing this, we can now add the zero to the right side of the dividend. So now we have a dividend of 40.
Here we will introduce a new term referred to as the “Remainder.” It is the number that remains after the incomplete division.
40 $ \div $ 11 $ \approx $ 3
Where:
11 x 3 = 33
We have a remainder of 7 after this step. So now we will again add zero to the remainder’s right to proceed with our solution. So now the remainder becomes 70.
70 $ \div $ 11 $ \approx $ 6
Where:
11 x 6 = 66
The Remainder we have now is 70 – 66 = 4. Again, we have a case of the remainder being less than the divisor, so it has to add zero to its right. By doing so, the remainder we have is 40. And there is no need to add the decimal point to the quotient because it has already been added there once.
40 $ \div $ 11 $ = 3
Where:
11 x 3 = 33
As a result, the provided mixed fraction 4/11 has a Quotient of 0.363 with the remainder being 7, obtained using the Long Division method.